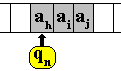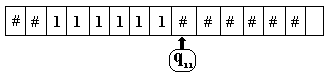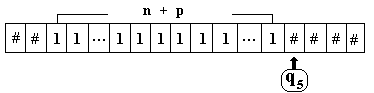Chap1.4 : Formalisation de la notion d'ordinateur

1.4.Formalisation de la notion d’ordinateur

Plan du chapitre:

1. La Machine de Turing théorique

1.1 Définition : machine de Turing

1.2 Définition : Etats de la machine

1.3 Définition : Les règles de la machine

2. La Machine de Turing physique

2.1 Constitution interne

2.2 Fonctionnement

2.3 Exemple : machine de Turing arithmétique

2.4 Machine de Turing informatique

MachTuring.dif\PMachTuring.exe

1. La Machine de Turing théorique

Entre 1930 et 1936 le mathématicien anglais A.Turing invente sur le papier une machine fictive qui ne pouvait effectuer que 4 opérations élémentaires que nous allons décrire. Un des buts de Turing était de faire résoudre par cette " machine " des problèmes mathématiques, et d’étudier la classe des problèmes que cette machine pourrait résoudre.

Définitions et notations (modèle déterministe)
Soit A un ensemble fini appelé alphabet défini ainsi :

A = { a₁,..., a_n} ( A ¹ Æ)
Soit W ={D,G} une paire

1.1 Définition : machine de Turing

Nous appellerons machine de Turing toute application T :

T : E ® N x ( W È A)
où E est un ensemble fini non vide, E Ì N x A

1.2 Définition : Etats de la machine

Nous appellerons E_t ensemble des états intérieurs de la machine T:
E_t = { q_i Î N , ($ a_i Î A / (q_i,a_i) Î Dom(T))
ou ($ x Î W / (q_i,x) Î Im(T)) }

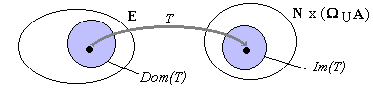
Dom(T) : domaine de définition de T.

Im(T) : image de T (les éléments T(a) de N x ( W È A),

pour a Î E)

Comme E est un ensemble fini, E_t est nécessairement un ensemble fini, donc il y a un nombre fini d’états intérieurs notés q_i.

1.3 Définition : Les règles de la machine

Nous appellerons " ensemble des règles " de la machine T, le graphe G de l’application T. Une règle de T est un élément du graphe G de T.

On rappelle que
G = {(a,b) Î E x [E_t x ( W È A)] / b = T(a) }

Notation : afin d’éviter une certaine lourdeur dans l’écriture nous conviendrons d’écrire les règles en omettant les virgules et les parenthèses.
Exemple : la règle ((q_i,a),(q_k,b)) est notée : q_ia q_kb

2. La Machine de Turing physique

2.1 Constitution interne

Nous construisons une machine de Turing physique constituée de :
G = {(a,b) Î E x [E_t x ( W È A)] / b = T(a) }

Une boîte notée UC munie d’une tête de lecture-écriture et d’un registre d’état.
Un ruban de papier supposé sans limite vers la gauche et vers la droite.
Sur le ruban se trouvent des cases contigües contenant chacune un seul élément de l’alphabet A.
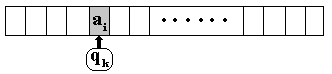
La tête de lecture-écriture travaille sur la case du ruban située devant elle ; elle peut lire le contenu de cette case ou effacer ce contenu et y écrire un autre élément de A.
Il existe un dispositif d’entraînement permettant de déplacer la tête de lecture-écriture d’une case vers la Droite ou vers la Gauche.
Dans la tête lecture-écriture il existe une case spéciale notée registre d’état, qui sert à recevoir un élément q_i de E_t.

2.2 Fonctionnement

Départ :

On remplit les cases du ruban d’éléments a_i de A.
On met la valeur " q_k " dans le registre d’état.
On positionne la tête sur une case contenant " a_i".

Actions : (la machine se met en marche)
La tête lit le " a_i". L’UC dont le registre d’état vaut " q_k ", cherche dans la liste des règles si le couple (q_k , a_i) Î Dom(T).
Si la réponse est négative on dit que la machine " bloque " (elle s’arrête par blocage).
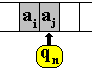
Si la réponse est positive alors le couple (q_k , a_i) a une image unique (machine déterministe)que nous notons (q_n , y). Dans ce couple, y peut avoir 3 types de valeurs possibles :

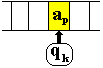
a) y=a_p ,dans ce cas la règle est donc de la forme q_ka_i q_na_p

a.1)L’UC fait effacer le a_i dans la case et le remplace par l’élément a_p.
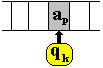
a.2) L’UC écrit q_n* dans le registre d’état en remplacement de la valeur q_k.*

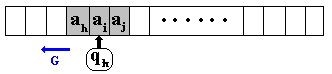
b) y = D , ici la règle est donc de la forme q_ka_i q_nD

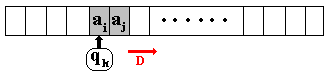
b.1) L’UC fait déplacer la tête vers la droite d’une case.
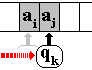
b.2) L’UC écrit q_n* dans le registre d’état en remplacement de la valeur q_k.*

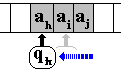
c) y = G , dans ce cas la règle est donc de la forme q_ka_i q_nG

c.1) L’UC fait déplacer la tête vers la gauche d'une case.
c.2) L’UC écrit q_n dans le registre d’état en remplacement de la valeur q_k.

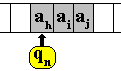
Puis la machine continue à fonctionner en recommençant le cycle des actions depuis le début : lecture du nouvel élément a_k etc...

2.3 Exemple : machine de Turing arithmétique

Nous donnons ci-dessous une machine T₁ additionneuse en arithmétique unaire.
A={#,1}

W ={D,G} un entier n est représenté par n+1 symboles " 1 " consécutifs (de façon à pouvoir représenter " 0 " par un unique " 1 ").

Etat initial du ruban avant actions

2 3

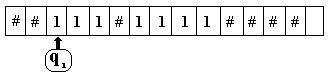
2 est représenté par 111
3 est représenté par 1111

Règles T₁: (application des règles suivantes pour simulation de 2+3)

q₁ 1 q₂D q₆ 1 q₇D q₁₁ 1 q₁₂#

q₂ 1 q₃D q₇ 1 q₈D q₁₂ # q₁₃G

q₃ 1 q₄D q₈ 1 q₉D q₁₃ 1 q₁₄#

q₄ # q₅1 q₉ 1 q₁₀D

q₅ 1 q₆D q₁₀ # q₁₁G

En démarrant la machine sur la configuration précédente on obtient :

Etat final du ruban après actions

5

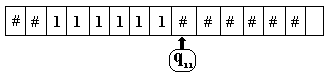
Cette machine ne fonctionne que pour additionner 2 et 3 ; il est facile d’en fournir une autre version plus générale T₂ fondée sur la même stratégie et le même état initial. Il suffit de construire des nouvelles règles.

Règles de T₂:

q₁ 1 q₁D q₃ 1 q₃#

q₁ # q₂1 q₃ # q₄G

q₂ 1 q₂D q₄ 1 q₅#

q₂ # q₃G

Cette machine de Turing laisse le ruban dans le même état final, mais elle est construite avec moins d’états intérieurs que la précédente.

En fait elle fonctionne aussi si la tête de lecture-écriture est positionnée sur n’importe lequel des éléments du premier nombre n.

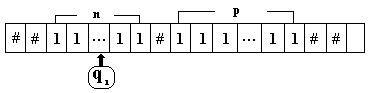
Etat initial sur le nombre de gauche

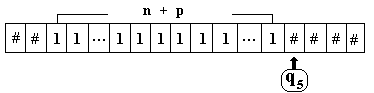
Etat final à la fin du nombre calculé (il y a n+p+1 symboles " 1 ")

Nous dirons que T₂ est plus " puissante " que T₁ au sens suivant :

T₂ a moins d’états intérieurs que T₁ .
T₂ permet d’additionner des entiers quelconques.
Il est possible de démarrer l’état initial sur n’importe lequel des " 1 " du nombre de gauche.

On pourrait toujours en ce sens chercher une machine T₃ qui posséderait la qualité b) de T₂ , mais qui pourrait démarrer sur n’importe lequel des " 1 " de l’un ou l’autre des deux nombres.

Nous voyons que ces machines sont capables d’effectuer des opérations, elles permettent de définir la classe des fonctions calculables (par machines de Turing).

Un ordinateur est fondé sur les principes de calcul d’une machine de Turing. J. Von Neumann a défini la structure générale d’un ordinateur à partir des travaux de A.Turing. Les éléments physiques supplémentaires que possède un ordinateur moderne n’augmentent pas sa puissance théorique. Les fonctions calculables sont les seules que l’on puisse implanter sur un ordinateur. Les périphériques et autres dispositifs auxiliaires extérieurs ou intérieurs n’ont pour effet que d’améliorer la " puissance " en terme de vitesse et de capacité. Comme une petite voiture de série et un bolide de formule 1 partagent les mêmes concepts de motorisation, de la même manière les différents ordinateurs du marché partagent les mêmes fondements mathématiques.

2.4 Machine de Turing informatique

A) C’est une machine de Turing dite normalisée :

L’alphabet A contient toujours le symbole " # "
L’ensemble des états E contient toujours deux états distingués q₀ (état initial) et q_f (état final).
La machine démarre toujours à l’état initial q₀ .
Elle termine sans blocage toujours à l’état q_f .
Dans les autres cas on dit que la machine " bloque ".

B)Algorithme d’une machine de Turing
C’est l’ensemble des règles précises qui définissent un procédé de calcul destiné à obtenir en sortie un " résultat " déterminé à partir de certaines " données " initiales.

C) Algorithme graphique d’une machine de Turing
Nous utilisons cinq classes de symboles graphiques

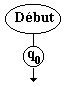
Positionne la tête de lecture sur le symbole voulu, met la machine à l’état initial q₀ et fait démarrer la machine.

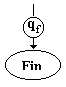Signifie que la machine termine correctement son calcul en s’arrêtant à l’état final q_f.

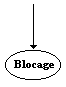
Aucune règle de la machine ne permetttant la poursuite du fonctionnement, arrêt de la machine sur un blocage.

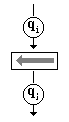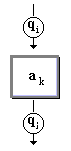
Déplacer la tête d’une case vers la gauche (la tête de lecture se positionne sur la case d’avant la case actuelle contenant le symbole a_p).
Correspond à la règle :
q_ia_p q_j G

Correspond à l’action à exécuter dans la deuxième partie de la règle :
q_i a_p q_j a_k
(la machine écrit a_k dans la case actuelle et passe à l’état q_j ).

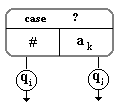Correspond à l’action à exécuter dans la première partie de la règle :
q_j a_k ...
ou q_i # ...
(la machine teste le contenu de la case actuelle et passe à l’état q_j ou à l’état q_i selon la valeur du contenu).

D) Organigramme d’une machine de Turing

On appelle organigramme d’une machine de Turing T, toute représentation graphique constituée de combinaisons des symboles des cinq classes précédentes.

Les règles de la forme q_n a_k q_n G ou q_na_kq_nD se traduisent par des schémas " bouclés " ce qui donne des organigrammes non linéaires.

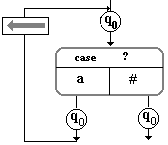
diagramme pour :q₀a q₀G
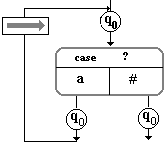
diagramme pour :q₀a q₀D

Exemple : organigramme de la machine T₂ normalisée(additionneuse n+p)
Règles de T₂ normalisée :

q₀ 1 q₀D	q₂ 1 q₂#
q₀ # q₁1	q₂ # q₃G
q₁ 1 q₁D	q₃ 1 q_f#
q₁ # q₂G

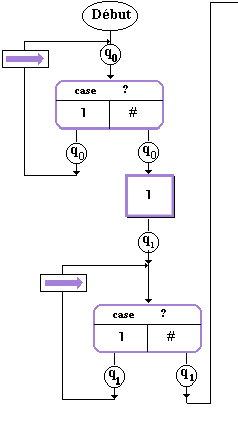
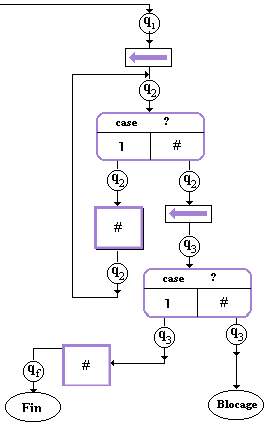Organigramme de la machine T₂ Nous voyons que ce symbolisme graphique est un outil de description du mode de traitement de l’information au niveau machine. C’est d’ailleurs historiquement d’une façon semblable que les premiers programmeurs décrivaient leur programmes.

q₁ 1 q₂D	q₆ 1 q₇D	q₁₁ 1 q₁₂#
q₂ 1 q₃D	q₇ 1 q₈D	q₁₂ # q₁₃G
q₃ 1 q₄D	q₈ 1 q₉D	q₁₃ 1 q₁₄#
q₄ # q₅1	q₉ 1 q₁₀D
q₅ 1 q₆D	q₁₀ # q₁₁G

q₁ 1 q₁D	q₃ 1 q₃#
q₁ # q₂1	q₃ # q₄G
q₂ 1 q₂D	q₄ 1 q₅#
q₂ # q₃G

	Positionne la tête de lecture sur le symbole voulu, met la machine à l’état initial q₀ et fait démarrer la machine.
	Signifie que la machine termine correctement son calcul en s’arrêtant à l’état final q_f.

	Aucune règle de la machine ne permetttant la poursuite du fonctionnement, arrêt de la machine sur un blocage.
	Déplacer la tête d’une case vers la gauche (la tête de lecture se positionne sur la case d’avant la case actuelle contenant le symbole a_p). Correspond à la règle : q_ia_p q_j G