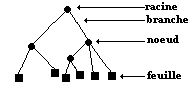
Un arbre est dit " étiqueté " si l’on nomme (attribution
d’un symbole de nom) sa racine et ses noeuds.
2. Spécification abstraite d'un arbre
binaire
e
Type Abstrait "ARBRE BINAIRE (étiqueté)"
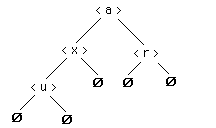
Il s'agit d'un arbre dont chaque noeud a au plus
deux descendants (un fils gauche noté filsg et/ou un fils
droit noté filsd).
sorte : Arbin
utilise : Noeud, Element
opérations :
Æ
: ®
Arbin
< -, -, - > : Noeud x Arbin x Arbin ®
Arbin
racine : Arbin ®Noeud
filsg : Arbin ®
Arbin
filsd : Arbin ®
Arbin
contenu : Noeud ®
Element
préconditions :
racine(A) def_ssi
A ¹ Æ
filsg(A) def_ssi
A ¹ Æ
filsd(A ) def_ssi
A ¹ Æ
axiomes :
"r
Î
noeud,"T1
Î
Arbin
,"T2
Î
Arbin
:
racine(<r,T1,T2
>) = r
filsg(<r,T1,T2
>) = T1
filsd(<r,T1,T2
>) = T2
contenu(r) Î
Element
Extensions immédiates
du Type abstrait Arbre Binaire
opérations :
taille : Arbin
®Entier
pere : Noeud ®
Noeud
racine : Arbin ®Noeud
frere : Noeud x Noeud ®
Booleen
hauteur : Noeud ®Entier
À
: ® Noeud
(racine principale)
préconditions :
pere(a) def_ssia¹À
frere(a,b) def_ssi(a¹À)
Ú
(b¹À
)
axiomes :
" r,s
Î
noeud,
"T1
Î
Arbin
, "T2
Î
Arbin,
"A
Î
Arbin
:
racine(filsg(<r,T1,T2
>)
)=
s Þ
pere(s)=r
racine(filsd(<r,T1,T2
>)
)= s Þ
pere(s)=r
< r,
<
À
,T1,T2
>
, A > = Æ
< r,
A,
<À
,T1,T2
>
>
= Æ
taille(Æ)=0
hauteur(À)=0
taille(<
r,T1,T2
>)
= 1+ taille(T1)
+ taille(T2)
"a,b
Î
noeud
pere(a) = pere(b) Þ
frere(a,b) = V
pere(a) ¹
pere(b)
Þ
frere(a,b) = F
pere(b) = a Þ
hauteur(b) = 1 + hauteur(a)
3. Implantation d'un arbre binaire par tableau
nterprétation par
une structure de données statique.
|
Interprétation-1, spécification
opérationnelle
|
On suppose connaître à l’avance le nombre maximum de noeuds
de l’arbre c-à-dire sa taille.
Le Type Abstrait de Données (TAD) choisi
est le couple tableau , variable.
Le schéma ci-dessous est une spécification opérationnelle
du TAD choisi sur un exemple :
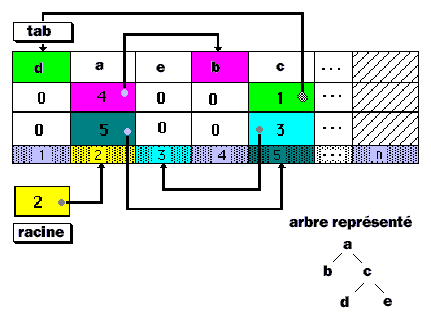
Implémentation-1, spécification
concrète
(structure statique de tableau en Pascal)
|
il est proposé la représentation concrète ci-dessous
:
Arbin @
type
Arbin=record
racine : 0..n;
tab : array[1..n] of record
val : Element;
g,d : O..n
end
end; |
Il est recommandé au lecteur de construire le programme
en implantant toutes les opérations du Type abstrait Arbre Binaire,
cette étude est intéressante car c’est une représentation
possible de la structure d’arbre dans les langages de programmation ne
disposant pas de la notion de pointeurs.
4. Implantation d'un arbre binaire par pointeurs
nterprétation par
une structure de données dynamique.
|
Interprétation-2, spécification
opérationnelle
|
Nous choisissons une autre version de
TAD par variable dynamique.
Le schéma ci-dessous est une spécification opérationnelle
du TAD choisi sur un exemple :
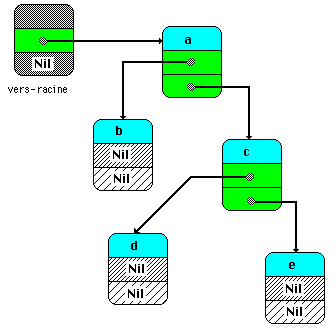
Implémentation-2, spécification
concrète
(structure dynamique de pointeurs en Pascal)
|
il est proposé la représentation ci-dessous, le noeud
se dénomme "arbre", pour le genre d'Element nous prendrons un type
char
:
Arbin @
type
parbre = ^arbre;
arbre = record
val : char ;
g,d : arbre
end;
Æ @ Nil
contenu(racine(A)) @
var
A : parbre; (A^.val)
filsg(A) @
var
A : parbre; (A^.g)
filsd(A) @
var
A : parbre; (A^.d) |
On est en allocation dynamique la taille est quelconque, l’implantation
ne pose aucun problème en Pascal. C'est donc ce
modèle que nous retenons pour implanter la notion de parcours d'arbre.
5. Différents algorithmes de parcours
d'un arbre binaire
n dénote parcours
d'un arbre général (binaire en particulier) tout algorithme
permettant de parcourir tous les noeuds de l'arbre une seule fois. Nous
distinguons 3 genre de parcours de type récursif :
-
le parcours en postordre ou postfixé.
-
le parcours en préordre ou préfixé
-
le parcours en ordre ou infixé.
La différence entre ces trois parcours est déterminé
par l'ordre dans lequel on examine la racine, le filsg et
le filsd.
| Lorsqu'on examine d'abord récursivement les filsg, puis
récursivement les filsd et enfin la racine nous dénommons
cette action parcours en postfixé. |
| Lorsqu'on examine d'abord récursivement les filsg, puis
la racine et enfin récursivement les filsd nous
dénommons cette action parcours en infixé. |
| Lorsqu'on examine d'abord la racine puis récursivement
les filsg et enfin récursivement les filsd nous dénommons
cette action parcours en préfixé. |
Procédures pascal implantant de tels algorithmes
On suppose que l'étiquette d'un noeud est une valeur de type
caractère (char):
type parbre = ^arbre;
arbre = record
val : char ;
g,d : arbre
end;
procedure postfixe (f: parbre);
begin
if f <> nil then
with f^ do
begin
postfixe(g);
postfixe(d);
write(val);
end
end; |
procedure infixe (f: parbre);
begin
if f <> nil then
with f^ do
begin
infixe(g);
write(val);
infixe(d);
end
end; |
procedure prefixe (f: parbre);
begin
if f <> nil then
with f^ do
begin
write(val);
prefixe(g);
prefixe(d)
end
end; |
Soit l'arbre binaire suivant :
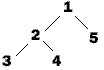
L'appel de la procédure postfixe sur cet arbre donne :
3 4 2 5 1
L'appel de la procédure infixe sur cet arbre donne :
3 2 4 1 5
L'appel de la procédure préfixe sur cet arbre donne :
1 2 3 4 5
6. L'exercice proposé
n donne l'arbre binaire
étiqueté ci-dessous :
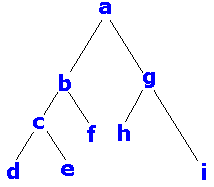
Votre travail consiste à exécuter manuellement sur votre
brouillon les 3 procédures postfixe, infixe et prefixesur
la variable f : parbre (où f est l'arbre binaire étiqueté
ci-haut). Le résultat est une suite de 9 caractères 'a b
c d ....'. Pour vous aider, les 3 réponses exactes figurent parmi
les 5 propositions suivantes qui vous sont faites :
Afin de tester votre solution cliquez sur un des rectangles colorés
des procédures de droite et faites un cliquer-glisser vers l'arbre
à gauche comme indiqué ci-dessous.
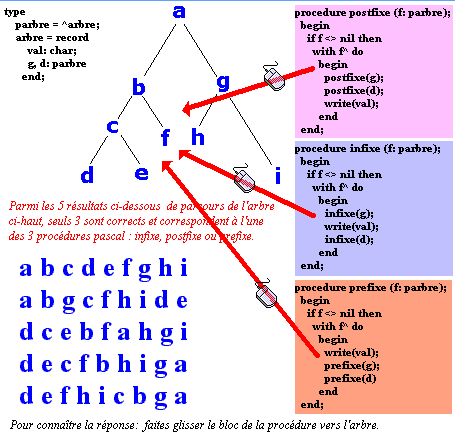
Le résultat exact apparaîtra surligné en couleur
parmi les 5 propositions.
'une manière générale,
un arbre est une structure de donnée informatique très utilisée
dans beaucoup de domaine et en particulier en algorithmique.