Recherche dans une table

Cliquez ici pour retourner aux thèmes d'exercices : ....

1. Algorithmes de recherche séquentielle dans une table
 

a première méthode pour rechercher un élément fixé dénomé clef dans une table consiste à faire une recherche séquentielle (ou linéaire). On examine successivement tous les éléments de la table et on regarde si l'on trouve un élément égal à l'élément fixé. Exemple de recherche d'un nom (string) fixé dans une table de 20 noms ( Array[1..20] of string ), la fonction renvoie le rang de la clef si elle a été trouvée sinon elle renvoie -1.

const N = 20 ;
type
 table = Array[1..N] of string ;

function Recherche (x: string ; nom : table): integer;
    var i: integer;
    begin
     Recherche := -1;
     for i := 1 to N do
        if x = nom[i] then begin
              Recherche := i ;
             Break ;
        end;
 end;

ne autre méthode de recherche en table est la recherche dichotomique. Supposons que notre table contienne des noms d'étudiants avec une note et qu'elle soit triée en ordre alphabétique. Au lieu de rechercher séquentiellement du premier jusqu'au dernier, on compare la clef à chercher au nom qui se trouve au milieu de la table des noms. Si c'est le même, on retourne la note de l'étudiant du milieu, sinon l'on recommence sur la première moitié (ou la deuxième) si le nom recherché est plus petit (ou plus grand) que le nom rangé au milieu de la table. Exemple de recherche d'un nom (string) fixé dans une table de 20 noms ( Array[1..20] of string ), la fonction renvoie le rang de la clef si elle a été trouvée sinon elle renvoie -1.

const N = 20 ;
type
 table = Array[1..N] of string ;

function Recherche (x: string ; nom : table): integer;
    var bas, milieu, haut: integer;
    begin
     bas := 1; haut := N;
     Recherche := -1;
     repeat
        milieu := (bas + haut) div 2;
        if x = nom[milieu] then
            Recherche := milieu
        else  if nom[milieu] < x then
                 bas := milieu + 1
               else
                  haut := milieu-1
    until (x = nom[milieu]) or (bas > haut);
 end;
 
 

n utilise aussi une autre méthode de recherche en table est le hachage. On utilise une fonction de hachage f(x) sur l'ensemble de toutes les clés possibles (les clefs sont souvent des chaînes de caractères comme dans le cas de la liste d'étudiants) dans un intervalle d'entiers. Pour une clef x la valeur f(x) est l'endroit où l'on trouve la clef x dans la table. Tout se passe parfaitement bien si f(x) est une application bijective. Pratiquement, on ne peut arriver à atteindre ce résultat et donc f(x) est rarement injective ce qui veut dire que nous choisirons des fonctions de hachage f(x) dans lesquelles des clefs différentes auront la même valeur (on appelle cela des collisions). On tente alors de minimiser le temps de calcul de f(x) ainsi que le nombre de collisions par le choix au coup par coup d'une fonction de hachage judicieuse.
 

'assistant vous propose d'exécuter à la main, pas à pas, le coeur principal de la boucle de recherche dichotomique dans un tableau de 20 entiers et dobserver le fonctionnement de l'algorithme. Vous devez rentrer une clef à chercher (dans la case Elt), puis ensuite cliquer sur le bouton [ Lancer la recherche dicho ], dans la fenêtre bleu de gauche l'assistant surligne la prochaine instruction du programme qu'il est prêt à exécuter. Un click sur le bouton [ pas suivant ] fait exécuter séquentiellement une instruction.

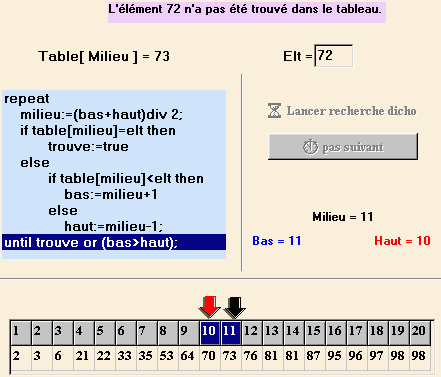
Dans l'exemple ci-dessus nous avons demandé la recherche de la clef 72 (du nombre 72) dans le tableau du bas. Les cases surlignées en bleu fonçé sont celles qui représentent l'intervalle de recherche actuel du programme [1,20]. Le principe dichotomique est de diviser cet intervalle en deux à chaque tours de boucle.

remier tours de boucle :

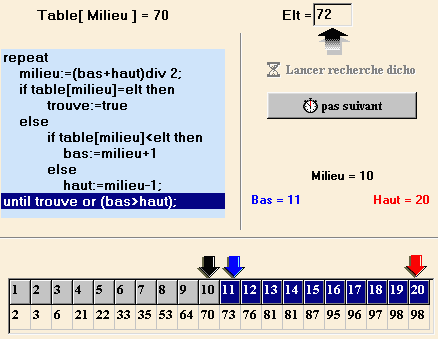
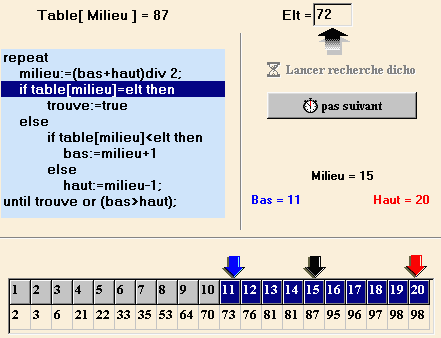
l'intervalle de recherche retenu est maintenant [11,20]
 

econd tours de boucle :

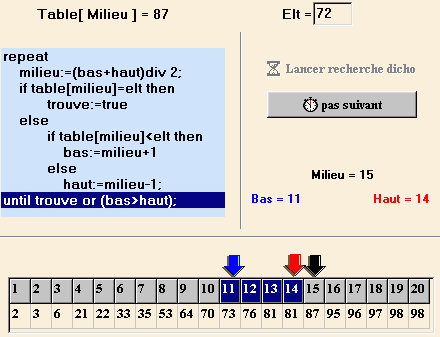
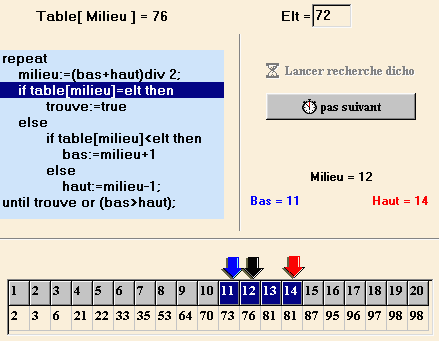
l'intervalle de recherche retenu est maintenant [11,14] etc...

inalement après la fin du dernier tours de boucle :

Ouf !