ARBRE ET EXPRESSIONS ARITHMETIQUES

Cliquez ici pour retourner aux thèmes d'exercices : ....

1. Expressions arithmétiques : une grammaire ambiguë

ous avons déjà vu au chapitre 2.3 du cours une grammaire possible pour les expressions arithmétiques simples, nous avons alors défini la notion d'arbre abstrait d'une telle expression. Rappellons l'exemple:
 

Gexp1 = (VN,VT,Axiome,Règles) VT = { 0, ..., 9, +,-, /, *, ), (} VN = { á  Expr ñ, á  Nbr ñ, á  Cte ñ, á  Oper ñ} Axiome : á  Expr ñ Règles : 1 :á  Expr ñ ¾® á  Nbr ñ | (á Expr ñ )| á  Expr ñ á Oper ñ  á Expr ñ 2 :á  Nbr ñ ¾® á  Cte ñ | á  Cte ñ á  Nbr ñ 3 :á  Cte ñ ¾® 0 | 1 |...| 9 4 :á  Oper ñ ¾® + | - | * | /

Les mots de L(G_exp1) sont des expressions de la forme (x+y-z)*x etc... où x, y, z sont des entiers.
 

Exemple : 327 - 8 est un mot de L(G_exp1)

Il n’a qu’un seul arbre de dérivation dans G_exp1 dessinons son arbre de dérivation :

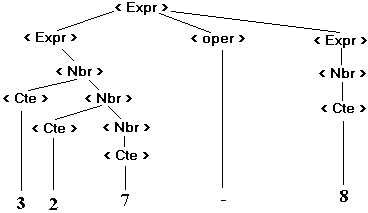
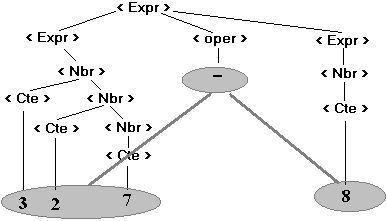
ous pouvons faire ressortir les liens abstraits qui relient les trois éléments terminaux 327, - et 8 :

L’arbre obtenu en grisé à partir de l’arbre de dérivation s’appelle l’arbre abstrait du mot " 327-8 ", nous le notons ainsi :

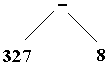
Cet arbre abstrait permet de manipuler la structure générale du mot facilement, tout en résumant la structure générale de l’arbre de dérivation. Cet arbre abstrait d'expressions est un arbre binaire

oici est une autre grammaire non ambigüe de ces expressions (écrites avec des lettres et des chiffres) que nous notons G_exp2   :
 

Gexp2 = (VN,VT,Axiome,Règles) VT = {0, ..., 9, a, ... ,z, +,-, /, *, ), (} VN = { á exprñ, á termeñ, á factñ,á lettreñ, á chiffreñ} Axiome : á exprñ Règles : 1 :<expr.> ::=<terme> | +<terme> | -<terme> 2 :<terme>::=<fact.> | *<fact.> | /<fact.> 3 :<fact.>::=<lettre> | <chiffre> | ( <expr.> ) 4 :<lettre>::= a |b |.....| z 5 :<chiffre>::= 0 |.....|9

Soit l’expression : a*(b+c)
 

voici son arbre de dérivation (arbre syntaxique) dans G :

 

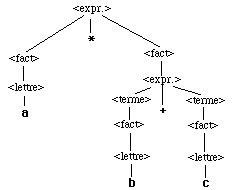
Il est alors possible de voir ce que pourrait être l’arbre abstrait associé :

 

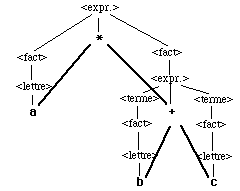
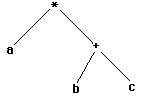
l’arbre abstrait est alors :

ans le cas des expressions il a été remarqué que la construction d’un arbre abstrait pour une expression est semblable à la traduction en forme postfixée, sans entrer dans les détails, c'est ce que fait le logiciel qui suit la démarche suivante :

- on construit un sous-arbre pour chaque expression,
- on construit un nouveau noeud pour chaque opérateur ainsi que pour chaque opérande
- les fils d’un noeud opérateur sont les racines des sous-arbres représentant les sous-expressions constituant les opérandes de cet opérateur.

Soit l’expression : a * ( b + 4 )
 

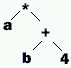
son arbre abstrait

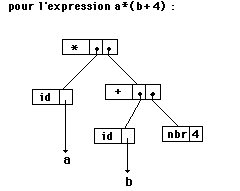
son implantation avec des pointeurs

Lorsqu'une telle expression  "a*(b+4)" est parcourue en postordre on obtient " a b 4 + * ", cette écriture appelé aussi notation polonaise inverse, est celle qui permet d'effectuer directement les calculs dans une machine à pile (comme en sont dotés la majorité des compilateurs) et en particulier les calculatrices HP.

es expressions arithmétiques consiérées ne sont construites qu'avec des lettres qui représentent des variables et les 4 opérateurs + , / , - , * .

Gex3 = (VN,VT,Axiome,Règles) VT = { a, ... ,z, +,-, /, *, ), ( } VN = { á exprñ, á termeñ, á factñ, á lettreñ } Axiome : á exprñ Règles : 1 :<expr.> ::=<terme> | +<terme> | -<terme> 2 :<terme>::=<fact.> | *<fact.> | /<fact.> 3 :<fact.>::=<lettre> | ( <expr.> ) 4 :<lettre>::= a |b |.....| z

Votre travail consiste à écrire une expression arithmétique selon la grammaire G_exp3 , àécrire sur votre brouillon un arbre abstrait de cette expression, puis à  parcourir en postordre l'arbre abstrait ainsi construit pour cette expression.

Pour vous aider le logiciel vous propose 3 expressions de la grammaire G_exp3 :
x + y
x * ( y + z )
( x - y )* z -( t + u )

Le logiciel vous montre pour chacune de ces 3 expressions l'arbre abstrait construit (figure ci-dessous) :

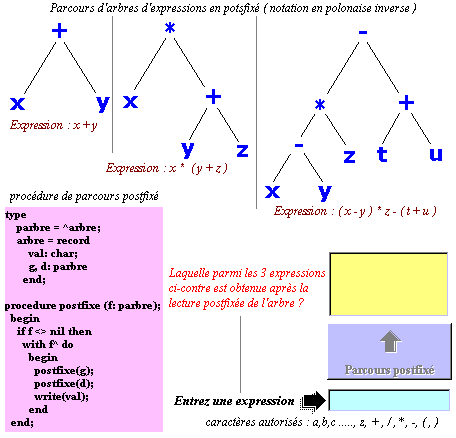
Parcourez chacun des arbres en ordre postfixé vous obtenez une chaîne, si vous voulez obtenir des indications de la part du logiciel effectuez comme indiqué ci-dessous un cliquer-glisser de l'arbre choisi, vers le rectangle coloré (en bas à gauche) contenant la procedure postfixe :

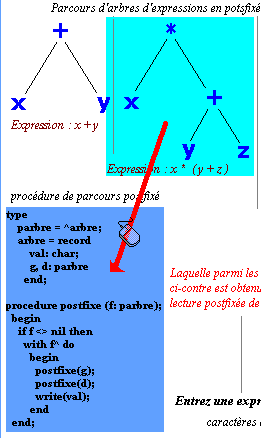
Lorsque vous relâcherez le cliquer-glisser (figure ci-dessous), le logiciel vous proposera 3 résultats de parcours postfixé possibles, un seul est correct à vous de trouver le bon.

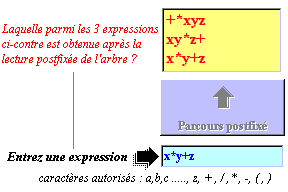
Lorsque vous cliquez sur l'une des 3 expressions dans le rectangle jaune, le logiciel vous indique d'une manière visuelle et sonore si votre choix est le bon !

ous pouvez aussi faire fonctionner le logiciel en mode analyseur d'expressions de la grammaire G_exp3 , il construira d'une manière interne un arbre abstrait puis effectuera son parcours postfixé et vous proposera 3 réponses possibles dont une seule sera correcte.

Exemple, vous entrez au clavier l'expression (a+b)*(c-(x/(y-u)+h))

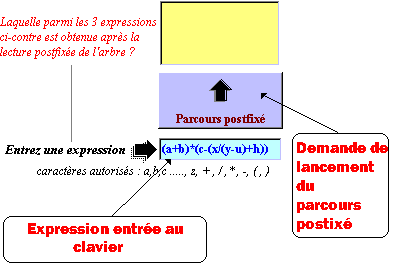
Après click sur le bouton de "parcours postfixé" :

Entraînez-vous !