1.2.Les circuits logiques
Plan
du chapitre: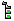
1.
Logique élémentaire pour l’informatique
1.1 Calcul propositionnel
naïf
1.2 Propriétés
des connecteurs logiques
1.3 Règles de déduction
2.
Algèbre de Boole
2.1 Axiomatique pratique
2.2 Exemples d’algèbre
de Boole
2.3 Notation des électroniciens
3.Circuits
booléens ou logiques
3.1 Principaux circuits
3.2 Fonction logique associée
à
un circuit
3.3 Circuit logique associé
à une fonction
3.4 Additionneur dans
l’UAL
3.5 Circuit multiplexeur
3.6 Circuit démultiplexeur
3.7 Circuit décodeur d'adresse
3.8 Circuit comparateur
3.9 Circuit bascule
3.10 Registre
3.11 Mémoires SRAM et DRAM
3.12 Afficheur à LED
3.13 Compteurs
3.14 Réalisation électronique de circuits booléens
 CircLogic.dif
(un simulateur de construction de circuits logiques)
CircLogic.dif
(un simulateur de construction de circuits logiques)
1.
Logique élémentaire pour l’informatique
1.1 Calcul propositionnel
naïf
Construire des programmes est
une activité scientifique fondée sur le raisonnement logique.
Un peu de logique simple va nous aider à disposer d’outils pratiques
mais rigoureux pour construire des programmes les plus justes possibles.
Si la programmation est un art, c’est un art rigoureux et logique. La rigueur
est d’autant plus nécessaire que les systèmes informatiques
manquent totalement de sens artistique.
Une proposition est une propriété
ou un énoncé qui peut avoir une valeur de vérité
vraie (notée V) ou fausse (notée F).
" 2 est un nombre impair " est
une proposition dont la valeur de vérité est F.
Par abus de langage nous noterons
avec le même symbole une proposition et sa valeur de vérité,
car seule la valeur de vérité d’une proposition nous intéresse
ici.
Soit l’ensemble P
= {V,F} des valeurs des propositions. On le munit de trois opérateurs
appelés connecteurs logiques : Ø
, Ù ,
Ú.
Ù
: P
x P®P
(se lit " et ")
Ú
: P
x P®P
(se
lit " ou ")
Ø
: P¾®P
(se lit " non ")
Ces connecteurs sont définis
en extension par leur tables de vérité :
| p |
q |
Ø
p |
p Ù
q |
p Ú
q |
| V |
V |
F |
V |
V |
| V |
F |
F |
F |
V |
| F |
V |
V |
F |
V |
| F |
F |
V |
F |
F |
1.2 Propriétés
des connecteurs logiques
-
Nous noterons p º
q , le fait la proposition p et la proposition q ont la même valeur
de vérité.
-
Le lecteur pourra démontrer
à l’aide des tables de vérité par exemple, que Ú
et Ù
possèdent les propriétés suivantes :
-
p Ú
q º q Ú
p
-
p Ù
q º q Ù
p
-
p Ú(q
Ú
r)
º (p
Ú
q)
Ú
r
-
p Ù
(q Ù
r) º (p
Ù
q)
Ù
r
-
p Ú
(q Ù
r) º (p
Ú
q)Ù (p
Ú
r)
-
p Ù
(q Ú
r) º (p
Ù
q)
Ú
(p
Ù
r)
-
p Ú
p º p
-
p Ù
p º p
-
ØØp
º
p
-
Ø(p
Ú
q)
º Ø
p Ù Ø
q
-
Ø
(p
Ù
q)
º Ø
p Ú Ø
q
-
Nous notons p Þ
q , la proposition : Ø
p Ú q
(l’implication).
Table de vérité
du connecteur Þ
:
| p |
q |
p Þ
q |
| V |
V |
V |
| V |
F |
F |
| F |
V |
V |
| F |
F |
V |
-
Il est aussi possible de prouver
des " égalités " de propositions en utilisant des combinaisons
de résultats précédents.
Exemple :Montrons
que : p Þ
q º Ø
q Þ Ø
p (implication contrapposée), par
définition et utilisation évidente des propriétés
:
p Þ
q º Ø
p Ú q
º
q ÚØ
p ºØ
(Ø q)
ÚØ
p ºØ
q ÞØ
p
1.3 Règles de déduction
Assertion :
c’est une proposition construite
à l’aide des connecteurs logiques (Ø
, Ù ,
Ú,
en
particulier) dont la valeur de vérité est toujours V (vraie).
Les règles de déduction
permettent de faire du calcul sur les assertions. Nous abordons
ici le raisonnement rationnel sous son aspect automatisable, en donnant
des règles d’inférences extraites du modèle du raisonnement
logique du logicien Gentzen. Elles peuvent être une aide très
appréciable lors de la construction et la spécification d’un
programme.
Les règles de déduction
sont séparées en deux membres. Le premier contient les prémisses
ou hypothèses de la règle, le deuxième membre est
constitué par une conclusion unique. Les deux membres sont séparés
par un trait horizontal. Gentzen classe les règles de déduction
en deux catégories : les règles d’introduction car il y a
utilisation d’un nouveau connecteur, et les règles d’éliminations
qui permettent de diminuer d’un connecteur une proposition.
Syntaxe d’une telle règle
:
Quelques règles de
déductions pratiques :
Règle d’introduction
du Ù
: |
Règle d’introduction
du Ú
: |
Règle d’introduction
du Þ : |
Règles d’élimination
du Ù
: , ,  |
Règle du modus ponens
: |
Règle du modus tollens
: |
Le système de
Gentzen contient d’autres règles sur le ou et sur le non. Enfin
il est possible de construire d’autres règles de déduction
à partir de celles-ci et des propriétés des connecteurs
logiques. Ces règles permettent de prouver la valeur de vérité
d’une proposition. Dans les cas pratiques l’essentiel des raisonnements
revient à des démonstrations de véracité d’implication.
La démarche est la
suivante : pour prouver qu’une implication est vraie, il suffit de
supposer que le membre gauche de l’implication est vrai et de montrer que
sous cette hypothèse le membre de droite de l’implication est vrai.
Exemple :
soit à montrer que la
règle de déduction R0 suivante est exacte
:
R0 : (transitivité
de Þ )
(transitivité
de Þ )
Hypothèse
: p est vrai
nous savons que : p Þ
q est vrai et que q Þ
r est vrai
-
En appliquant le modus ponens :
 nous
déduisons que : q est vrai.
nous
déduisons que : q est vrai.
-
En appliquant le modus ponens à
(q , q Þ
r) nous
déduisons que : r est vrai.
-
Comme p est vrai (par hypothèse)
on applique la règle d’introduction de Þ
sur (p , r) nous
déduisons que :p Þ
r est vrai (cqfd).
Nous avons prouvé que
R0
est
exacte. Ainsi nous avons construit une nouvelle règle de déduction
qui pourra nous servir dans nos raisonnements.
Nous avons montré un des
outils de construction raisonnée de programmes. La logique interne
des ordinateurs est encore actuellement plus faible puisque basée
sur la logique booléenne, en attendant que les machines de 5ème
génération basées sur la logique du premier ordre
(logique des prédicats, supérieure à la logique propositionnelle)
soient définitivement opérationnelles.
2.
Algèbre de Boole
2.1 Axiomatique pratique
Du nom du mathématicien
anglais G.Boole qui l’inventa. Nous choisissons une axiomatique compacte,
l’axiomatique algébrique :
On appelle algèbre
de Boole tout ensemble E muni de :
-
deux lois de compositions internes
·
et
Å,
-
une application involutive f (f2
= Id ) de E dans lui-même,notée

-
chacune des deux lois ·
, Å, est
associative et commutative,
-
chacune des deux lois est distributive
par rapport à l’autre,
-
la loi ·
admet un élément neutre unique noté e1,
"xÎE,
x·
e1
= x
-
la loi Å admet
un élément neutre noté e0,
"xÎE,
xÅ
e0
= x
-
tout élément de E est idempotent pour chacune des deux
lois :
"xÎE,
x
·
x
= x et x Åx
= x
-
axiomes de complémentarité
:

 "x,yÎE2,
"x,yÎE2, 
"x,yÎE2, 
2.2 Exemples d’algèbre
de Boole
a)
L’ensemble P(E) des parties d’un ensemble E, muni des opérateurs
intersection Ç
,union
È, et l’application
involutive complémentaire dans E CE( )
)
b)
L’ensemble des propositions (leurs valeurs {V,F}) muni des connecteurs
logiques Ø
(l’application
involutive) , Ù , Ú .
Il suffit de vérifier
les axiomes précédents en substituant les lois du nouvel
ensemble E aux lois ·
, Å et  .
Il est montré en mathématiques que toutes les algèbres
de Boole finies sont isomorphes à un ensemble (P(E),
Ç,
È , CE):
elles sont donc de cardinal 2n
.
Il est montré en mathématiques que toutes les algèbres
de Boole finies sont isomorphes à un ensemble (P(E),
Ç,
È , CE):
elles sont donc de cardinal 2n
2.3 Notation des électroniciens
L’algèbre des circuits
électriques est une algèbre de Boole :
L’ensemble E={0,1} muni des
lois " . " et " + " et de l’application complémentaire  .
.
Formules pratiques et utiles
(résultant de l’axiomatique) :
a + 1 = 1
a + 0 = a
a + a = a
 =
1 =
1
 = = 
 |
a.1 = a
a.0 = 0
a.a = a
 =
0 =
0
 = = 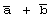
 |
Formule d’absorbtion :
| a+(b.a) = a.(a+b) = (a+b).a
= a+b.a = a |
Montrons par exemple : a+(b.a)=a
a+(b.a)= a+a.b = a.1+a.b = a.(1+b)
= a.1 = a
Le reste se montrant de la même
façon.
Cette algèbre est utile
pour décrire et étudier les schémas électroniques,
mais elle sert aussi dans d’autres domaines que l’électricité.
Elle est étudiée ici parce que les ordinateurs actuels sont
basés sur des composants électroniques. Nous allons descendre
un peu plus bas dans la réalisation interne du cœur d’un ordinateur,
afin d’aboutir à la construction d’un additionneur en binaire dans
l’UAL.
Tables de vérité
des trois opérateurs :
| x |
y |
 |
x
. y |
x
+ y |
| 1 |
1 |
0 |
1 |
1 |
| 1 |
0 |
0 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
| 0 |
0 |
1 |
0 |
0 |
3.Circuits
booléens ou logiques
Nous représentoons par
une variable booléenne x le passage d’un courant électrique.
Lorsque x=0, nous dirons que x est à l’état 0 (le courant
ne passe pas) ; lorsque x=1, nous dirons que x est à l’état
1 (le courant passe.)
Une telle variable booléenne
permet ainsi de visualiser, sous forme d’un bit d’information (0,1)le comportement
d’un composant physique laissant ou ne laissant pas passer le courant.
Nous ne nous préoccuperons
pas du type de circuits électriques permettant de construire un
circuit logique (les composants électriques sont basés sur
les circuits intégrés). Nous ne nous intéresserons
qu’à la fonction logique (booléenne) associée à
un tel circuit. En fait un circuit logique est un opérateur d’une
algèbre de Boole ( c’est-à-dire une combinaison de symboles
de l’algèbre{0,1},.,+, ).
).
3.1 Principaux
circuits
Nous proposons donc 3 circuits
logiques de base correspondant aux deux lois internes et à l’opérateur
de complémentation involutif.
Le circuit OU associé
à la loi " + " :
 la
table de vérité est celle du +
la
table de vérité est celle du +
Le circuit ET associé
à la loi " . " :
 la table de vérité est celle du .
la table de vérité est celle du .
Le circuit NON associé
à la loi "  " :
" :
 la table de vérité est celle du
la table de vérité est celle du 
On construit deux circuits
classiques à l’aide des précédents :
L’opérateur XOR =
" ou exclusif " :
 schéma :
schéma : 
Dont voici la table de vérité
:
| a |
b |
 |
| 1 |
1 |
0 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
0 |
L’opérateur NAND (le
NON-ET):
 schéma :
schéma : 
Dont voici la table de vérité
:
| a |
b |
 |
| 1 |
1 |
0 |
| 1 |
0 |
1 |
| 0 |
1 |
1 |
| 0 |
0 |
1 |
3.2 Fonction logique associée
à un circuit
 |
Un circuit
logique est un système de logique séquentielle où
la valeur de sortie S(état de la variable booléenne S
de sortie) dépend des valeurs des entrées e1,e2,...,en(états
des variables booléennes ei d’entrées). Sa valeur
de sortie est donc une fonction S = f(e1,e2,...,en). |
Pour calculer f à partir
d’un schéma de circuits logiques, il suffit d’indiquer à
la sortie de chaque opérateur (circuit de base) la valeur de l’expression
booléenne en cours. Puis, à la fin, nous obtenons une expression
booléenne que l’on simplifie à l’aide des axiomes ou des
théorèmes de l’algèbre de Boole.
Exemple :

En simplifiant S
: (a+b).b+ = b +
= b +  (formule d’absorbtion)
(formule d’absorbtion)
b +  = 1.
= 1.
3.3 Circuit logique associé
à une fonction
A l’inverse, la création
de circuits logiques à partir d’une fonction booléenne f
à n entrées est aussi simple. Il suffit par exemple, dans
la fonction, d’exprimer graphiquement chaque opérateur par un circuit,
les entrées étant les opérandes de l’opérateur.
En répétant l’action sur tous les opérateurs, on construit
un graphique de circuit logique associé à la fonction f.
Exemple : Soit f(a,b,c)=(a+b)+(b.c)
Construction progressive du
circuit associé.
1°) opérateur " +
" :

2°) branche supérieure
de l’opérateur " + " :

3°) branche inférieure
de l’opérateur " + " :

3.4 Additionneur dans l’UAL
a)
Demi-additionneur
Reprenons les tables de vérités
du "  "(Xor),
du " + " et du " . " et adjoignons la table de calcul de l’addition en
numération binaire.
"(Xor),
du " + " et du " . " et adjoignons la table de calcul de l’addition en
numération binaire.
Tout d’abord les tables comparées
des opérateurs booléens :
| a |
b |
 |
a+b |
a.b |
| 1 |
1 |
0 |
1 |
1 |
| 1 |
0 |
1 |
1 |
0 |
| 0 |
1 |
1 |
1 |
0 |
| 0 |
0 |
0 |
0 |
0 |
ensuite la table d’addition
en numération binaire :
0(1)
représente la retenue 1 à reporter.
En considérant une addition
binaire comme la somme à effectuer de deux mémoires à
un bit, nous observons dans l’addition binaire les différentes configurations
des bits concernés (notés a et b).
Nous aurons comme résultat un bit de somme et un bit
de retenue :
| bit a |
bit b |
bit somme |
bit de retenue |
| 1 + |
1 = |
0 |
1 |
| 1 + |
0 = |
1 |
0 |
| 0 + |
1 = |
1 |
0 |
| 0 + |
0 = |
0 |
0 |
Si l’on compare avec les tables
d’opérateurs booléens, on s’aperçoit que l’opérateur
"  "(Xor)
fournit en sortie les mêmes configurations que le bit de somme, et
que l’opérateur " . "(Et) délivre en sortie les mêmes
configurations que le bit de retenue. Il est donc possible de simuler une
addition binaire (arithmétique binaire) avec les deux opérateurs
"
"(Xor)
fournit en sortie les mêmes configurations que le bit de somme, et
que l’opérateur " . "(Et) délivre en sortie les mêmes
configurations que le bit de retenue. Il est donc possible de simuler une
addition binaire (arithmétique binaire) avec les deux opérateurs
"  " et
" . ". Nous venons de construire un demi-additionneur ou additionneur sur
un bit. Nous pouvons donc réaliser le circuit logique simulant la
fonction complète d’addition binaire, nous l’appelerons " additionneur
binaire "(somme arithmétique en binaire de deux entiers en binaire).
" et
" . ". Nous venons de construire un demi-additionneur ou additionneur sur
un bit. Nous pouvons donc réaliser le circuit logique simulant la
fonction complète d’addition binaire, nous l’appelerons " additionneur
binaire "(somme arithmétique en binaire de deux entiers en binaire).

schéma logique d’un
demi-additionneur
b)Additionneur
complet
Une des constructions les plus
simples et la plus pédagogique d’un additionneur complet est de
connecter entre eux et en série des demi-additionneurs (additionneurs
en cascade). Il existe une autre méthode dénommée
" diviser pour régner " pour construire des additionneurs complets
plus rapides à l’exécution que les additionneurs en cascade.
Toutefois un additionneur en cascade pour UAL à 32 bits, utilise
2 fois moins de composants électroniques qu’un additionneur diviser
pour régner.
Nous concluons donc qu’une UAL
n’effectue en fait que des opérations logique (algèbre de
Boole) et simule les calculs binaires par des combinaisons d’opérateurs
logiques.
Soient a et b deux nombres binaires
à additionner dans l’UAL. Nous supposons qu’ils sont stockés
chacun dans une mémoire à n bits. Nous notons apet
bp
leur bit respectif de rang p. Lors de l’addition il faut non seulement
additionner les bits ap et bp à
l’aide d’un demi-aditionneur, mais aussi l’éventuelle retenue notée
Rp
provenant du calcul du rang précédent.

additionneur en cascade (addition
sur le bit de rang p)
On réadditionne Rp
à l’aide d’un demi-additionneur à la somme de apet
bpet
l’on obtient le bit de somme du rang p noté
Sp. La propagation
de la retenue Rp+1 est faite par un " ou " sur les deux
retenues de chacun des demi-additionneurs et passe au rang p+1. Le processus
est itératif sur tous les n bits des mémoires contenant les
nombres a et b.
Si l’UAL effectue des additions
sur 32 bits, il y aura 32 circuits comme le précédent, tous
reliés en série pour la propagation de la retenue.
 APIUal.dif
(un exemple d'additionneur interactif sur 4 bits)
APIUal.dif
(un exemple d'additionneur interactif sur 4 bits)
Notation du circuit additionneur sur 2 bits :

Remarque :
Ce circuit
d'addition sur 2 bits engendre en fait en plus des bits de somme un troisième
bit de retenue qui sera généralement mémorisé dans le bit de retenue (bit
de carry noté C) du mot d'état programme ou PSW (Progral Status Word) du
processeur. C'est le bit C de ce mot qui est consulté par exemple afin de
savoir si l'opération d'addition a généré un bit de retenu ou non.
|

3.5 Circuit multiplexeur (circuit combinatoire)
C'est un circuit d'aiguillage comportant 2n
entrées, n lignes de sélection et une seule sortie. Les n lignes de sélection
permettent de "programmer" le numéro de l'entrée qui doit être sélectionnée
pour sortir sur une seule sortie (un bit). La construction d'un tel circuit
nécessite 2n circuits "et", n circuits "non" et 1 circuit "ou".
Notation du multiplexeur :

3.6 Circuit démultiplexeur (circuit combinatoire)
C'est
un circuit qui fonctionne à l'inverse du circuit précédent, il permet d'aiguiller
une seule entrée (un bit) sur l'une des 2n sorties possibles, selon la "programmation"( l'état ) de ses n lignes de sélection.
Notation du démultiplexeur :

3.7 Circuit décodeur d'adresse (circuit combinatoire)
C'est un circuit composé de n lignes d'entrées qui représentent une adresse sur n bits et de 2n
lignes de sortie possibles dont une seule est sélectionnée
en fonction de la "programmation" des n lignes d'entrées.
Notation du décodeur d'adresse :

Exemple d'utilisation d'un décodeur d'adresse à 8 bits :
On entre l'adresse de la ligne à sélectionner soit 10100010 ( A0 =1 , A1 = 0, A2 = 1, … , A7 = 0 ) ce nombre binaire vaut 162 en décimal, c'est donc la sortie S162 qui est activée par le composant comme le montre la figure ci-dessous.

La construction d'un circuit décodeur d'adresse à n bits nécessite 2n
circuits "et", n circuits "non". Ce genre de circuits très fréquent dans
un ordinateur sert à sélectionner des registres, des cellules mémoires ou
des lignes de périphériques.
3.8 Circuit comparateur (circuit combinatoire)
C'est
un circuit réalisant la comparaison de deux mots X et Y de n bits chacun
et sortant une des trois indication possible X+Y ou bien X>Y ou X<Y.
Il possède donc 2n entrées et 3 sorties.
Notation du comparateur de mots à n bits :

3.9 Circuit bascule (circuit à mémoire)
C'est
un circuit permettant de mémoriser l'état de la valeur d'un bit. Les bascules
sont les principaux circuits constituant les registres et les mémoires dans
un ordinateur.
Les principaux types de bascules sont RS, JK et D,
ce sont des dispositifs chargés de "conserver" la valeur qu'ils viennent
de prendre.
Schéma électronique et notation de bascule RS minimale théorique :
|

|

notation |
Table de vérité associée à cette bascule :
|
R |
S |
Qt+dt |
Qt représente la valeur de la sortie au temps t , Qt+dt représente la valeur de cette même sortie un peu plus tard au temps t+dt.
L'état R=1 et S=1 n'est pas autorisé
L'état R=0 et S=0 fait que Qt+dt = Qt , la sortie Q conserve la même valeur au cours du temps, le circuit "mémorise" donc un bit.
|
|
1 |
1 |
------ |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
Qt |
Si l'on veut que le circuit mémorise un bit égal à
0 sur sa sortie Q, on applique aux entrées les valeurs R=1 et S=0
au temps t0, puis à t0+dt
on applique les valeurs R=0 et S=0. Tant que les entrées R et S restent à
la valeur 0, la sortie Q conserve la même valeur (dans l'exemple Q=0).
En pratique ce sont des bascules RS synchronisées
par des horloges (CLK pour clock) qui sont utilisées, l'horloge sert alors
à commander l'état de la bascule. Seule la sortie Q est considérée.
Dans une bascule RS synchronisée, selon que le top
d'horloge change d'état ou non et selon les valeurs des entrées R et S soit
d'un top à l'autre la sortie Q du circuit ne change pas soit la valeur du
top d'horloge fait changer (basculer) l'état de la sortie Q.
Schéma électronique général et notation d'une bascule RS synchronisée :
|

|

notation |
Remarque :
Certains types de mémoires ou les registres dans
un ordinateur sont conçus avec des variantes de bascules RS (synchronisées)
notée JK ou D
|
Schéma électronique général et notation d'une bascule de type D :
|

|

notation |
Fonctionnement pratique d'une telle bascule D dont
les entrées sont reliées entre elles. Supposons que la valeur de l'entrée
soit le booléen x (x=0 ou bien x=1) et que l'horloge soit à 0.

En simplifiant le schéma nous obtenons une autre
présentation faisant apparaître la bascule RS minimale théorique décrite
ci-haut :

Or la table de vérité de cet élément lorsque les
entrées sont égales à 0 indique que la bascule conserve l'état antérieur
de la sortie Q:
Conclusion pour une bascule D :
Lorsque l'horloge est à 0, quelque soit la valeur
de l'entrée D (D=0 ou D=1) une bascule D conserve la même valeur sur la sortie
Q.
|
Que se passe-t-il lorsque lors d'un top d'horloge celle-ci passe à la valeur 1 ?
Reprenons le schéma simplifié précédent
d'une bascule D avec une valeur d'horloge égale à 1.

Nous remarquons que sur les entrée R et S nous trouvons la valeur x et son complément `x ,
ce qui élimine deux couples de valeurs d'entrées sur R et S (R=0 , S=0) et
(R=1 , S=1). Nous sommes sûrs que le cas d'entrées non autorisé par un circuit
RS (R=1 , S=1) n'a jamais lieu dans une bascule de type D. Il reste à envisager
les deux derniers couples (R=0 , S=1) et (R=1 , S=0). Nous figurons ci-après
la table de vérité de la sortie Q en fonction de l'entrée D de la bascule
(l'horloge étant positionnée à 1) et pour éclairer le lecteur nous avons
ajouté les deux états associés des entrées internes R et S :
|
x |
R |
S |
Q |
Nous remarquons que la sortie Q prend la valeur de l'entrée D (D=x ), elle change donc d'état.
|
|
0 |
1 |
0 |
0 |
|
1 |
0 |
1 |
1 |
Conclusion pour une bascule D :
Lorsque l'horloge est à 1, quelque soit la valeur
de l'entrée D (D=0 ou D=1) une bascule D change et prend sur la sortie Q
la valeur de l'entrée D
|
3.10 Registre (circuit à mémoire)
Un registre
est un circuit qui permet la mémorisation de n bits en même temps. Il existe
dans un ordinateur plusieurs variétés de registres, les registres parallèles,
les registres à décalage (décalage à droite ou décalage à gauche) les registres
séries.
Les bascules de type D sont les plus utilisées pour construire
des registres de différents types en fonction de la disposition des
entrées et des sorties des bascules : les registres à entrée
série/sortie série, à entrée série/sortie
parallèle, à entrée parallèle/sortie parallèle,
à entrée parallèle/sortie série.
Voici un exemple de registre à n entrées parallèles (a0,a1,…,an-1) et à n sorties parallèles (s0,s1,…,sn-1) construit avec des bascules de type D :

Examinons le fonctionnement de ce "registre parallèle à n bits"
La ligne CLK fournit le signal d'horloge, la ligne RAZ permet l'effacement de toutes les sorties sk du registre, on dit qu'elle fournit le signal de validation :
- Lorsque RAZ = 0 on a (s0=0, s1=0, …, sn-1=0)
- Lorsque RAZ = 1 on a (s0= q0, s1= q1, …, sn-1= qn-1)
Donc RAZ=0 sert à effacer tous les bits de sortie du registre, dans le cas où RAZ=1 qu'en est-il des sorties sk. D'une manière générale nous avons par construction sk = RAZ . qk :
- Tant que CLK = 0 alors, comme RAZ=1 nous avons sk = qk (qk est l'état antérieur de la bascule). Dans ces conditions on dit que l'on "lit le contenu actuel du registre".
- Lorsque CLK = 1 alors, tous les qk basculent et chacun d'eux prend la nouvelle valeur de son entrée ak. Comme RAZ=1 nous avons toujours sk = qk (qk
est le nouvel état de la bascule). Dans ces conditions on dit que
l'on vient de "charger le registre" avec une nouvelle valeur.
Notations des différents type de registres :
|

registre série/série |

registre série/parallèle |
|

registre parallèle/série |

registre parallèle/parallèle |
Registre à décalage
C'est un registre
à entrée série ou parallèle qui décale de 1 bit tous les bits d'entrée soit
vers "la droite" (vers les bits de poids faibles), soit vers "la gauche"
(vers les bits de poids forts). Un registre à décalage dans un ordinateur
correspond soit à une multiplication par 2 dans le cas du décalage à gauche,
soit à une division par 2 dans le cas du décalage à droite.
|
Conclusion mémoire-registre
Nous remarquons donc
que les registres en général sont des mémoires construites avec des bascules
dans lesquelles on peut lire et écrire des informations sous forme de bits.
Toutefois dès que la quantité d'information à stocker est très grande les
bascules prennent physiquement trop de place (2 NOR, 2 AND et 1 NON). Actuellement,
pour élaborer une mémoire stockant de très grande quantité d'informations,
on utilise une technologie plus compacte que celle des bascules, elle est
fondée sur la représentation d'un bit par 1 transistor et 1 condensateur.
Le transistor réalise la porte d'entrée du bit et la sortie du bit, le condensateur
selon sa charge réalise le stockage du bit.
Malheureusement un condensateur ne conserve pas sa
charge au cours du temps (courant de fuite inhérent au condensateur), il
est alors indispensable de restaurer de temps en temps la charge du condensateur
(opération que l'on dénomme rafraîchir la mémoire) et cette opération
de rafraîchissement mémoire a un coût en temps de réalisation. Ce qui veut
donc dire que pour le même nombre de bits à stocker un registre à bascule
est plus rapide à lire ou à écrire qu'une mémoire à transistor, c'est pourquoi
les mémoires internes des processeurs centraux sont des registres.
3.11 Mémoire SRAM et mémoire DRAM
Dans un ordinateur actuel coexistent deux catégories de mémoires :
1°) Les mémoires statiques SRAM élaborées à l'aide
de bascules : très rapides mais volumineuses (plusieurs transistors pour
1 bit).
2°) Les mémoires dynamiques DRAM élaborées avec un
seul transistor couplé à un condensateur : très facilement intégrables dans
une petite surface, mais plus lente que les SRAM à cause de la nécessité
du rafraîchissement.
Voici à titre indicatif des ordres de grandeur actuels qui peuvent
varier avec les innovations technologiques rapides en ce domaine :
SRAM temps d'accès à une information : 5 nanosecondes
DRAM temps d'accès à une information : 50 nanosecondes
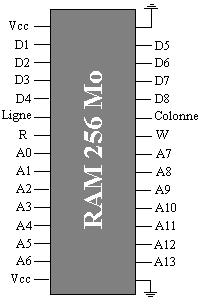
Fonctionnement d'une DRAM de 256 Mo fictive
|
La mémoire physique aspect extérieur :

Le schéma général de la mémoire :
|
|
Vcc = alimentation électrique
D1 à D8 = bits de données (1 octet ici)
Ligne, Colonne = lignes de sélection soit d'une adresse de ligne soit d'une adresse de colonne
W = autorisation d'écriture
R = validation de lecture
A0, … , A13 = adresse d'une ligne ou adresse d'une colonne
 = symbole de mise à la masse
= symbole de mise à la masse
|
Nous adoptons une vision abstraite de l'organisation interne de cette mémoire sous forme d'une matrice de 214 lignes et 214 colonnes soient en tout 214. 214= 228 cellules de 1 octet chacune (228 octets = 28. 220 o = 256 . 220 o = 256 Mo, car 1 Mo = 220 o)
Ce qui donne une matrice de 16384 lignes et 16384 colonnes, numérotées par exemple de 20 = 1 jusqu'à 214 = 16384, selon la figure ci-dessous :
|

|
Dans l'exemple à gauche :
La sélection d'une ligne de numéro m donné (d'adresse m-1 donnée) et d'une colonne de numéro k donné (d'adresse k-1 donnée) permet de sélectionner directement une cellule contenant 8 bits.

|
Exemple de sélection de ligne dans la matrice mémoire
à partir d'une adresse (A0, … , A13) , dans notre exemple théorique la ligne
de numéro 20 = 1 a pour adresse (0,0,…,0) et la ligne de numéro 214 =
16384 a pour adresse (1,1,…,1). Lorsque l'adresse de sélection d'une ligne
arrive sur les pattes (A0, … , A13) de la mémoire elle est rangée dans un
registre interne (noté tampon) puis passée à un circuit interne du type décodeur
d'adresse à 14 bits (14 entrées et 214 = 16384 sorties) qui sélectionne la ligne adéquate.

Il en va de même pour la sélection d'une colonne :

La sélection d'une ligne, puis d'une colonne permet
d'obtenir sur les pattes D, D2, …, D8 de la puce les 8 bits sélectionnés.
Ci dessous une sélection en mode lecture d'une cellule de notre mémoire de
256 Mo :

Il est possible aussi d'écrire dans une cellule de
la mémoire selon la même démarche de sélection. Pour opérer une lecture il
faut que la ligne de validation R de la mémoire soit activée, pour opérer une écriture, il faut que la ligne de validation W de la mémoire soit activée.
En attendant une nouvelle technologie (optique, quantique,
organique,…) les constituants de base d'un ordinateur sont fondés sur l'électronique
à base de transistor découverts à la fin des années quarante. De nos jours
deux technologie de transistor sont présentes sur le marché : la technologie
TTL (Transistor Transistor Logic) la plus ancienne et la technologie MOS
(Metal Oxyde Semi-conductor).
3.12 Afficheur LED à 7 segments
On utilise
dans les ordinateurs des afficheurs à LED, composés de 7 led différentes
qui sont allumées indépendamment les unes des autres, un circuit décodeur
à 3 bits permet de réaliser simplement cet affichage :

3.13 Compteurs
Ce sont des circuits chargés d'effectuer un comptage cumulatif de divers signaux.
Par exemple considérons un compteur sur 2 bits avec
retenue éventuelle, capable d'être activé ou désactivé, permettant de compter
les changement d'état de la ligne d'horloge CLK. Nous proposons d'utiliser
deux demi-additionneurs et deux bascules de type D pour construire le circuit.
|

|
Le circuit compteur de gauche possède deux entrées En et CLK, il possède trois sorties a0, a1 et carry.
Ce compteur sort sur les bits a0, a1 et sur le bit de carry le nombre de changements en binaire de la ligne CLK (maximum 4 pour 2 bits) avec retenue s'il y a lieu.
La ligne d'entrée En est chargée d'activer ou de désactiver le compteur
Notation pour ce compteur :

|
Fonctionnement de l'entrée En (enable) du compteur précédent :
- Lorsque En = 0, sur la première bascule en entrée D nous avons D = a0 Å 0 (or nous savons que : "x, x Å 0 = x ), donc D = a0 et Q ne change pas de valeur. Il en est de même pour la deuxième bascule et son entrée D vaut a1. Donc quoiqu'il se passe sur la ligne CLK les sorties a0 et a1 ne changent pas, on peut donc dire que le comptage est désactivé lorsque le enable est à zéro.
- Lorsque En = 1, sur la première bascule en entrée D nous avons D = a0 Å 1 (or nous savons que : "x, x Å 1 = `x ), donc Q change de valeur. On peut donc dire que le comptage est activé lorsque le enable est à un.
Utilisons la notation du demi-additionneur pour représenter ce compteur à 2 bits :
|

un demi-additionneur |

le compteur à 2 bits |
En généralisant à la notion de compteur à n bits nous obtenons le schéma ci-après :

3.14 Réalisation électronique de circuits booléens
Dans ce
paragraphe nous indiquons pour information anecdotique au lecteur, à partir
de quelques exemples de schémas électroniques de base, les réalisation physiques
possibles de différents opérateurs de l'algèbre de Boole.
Le transistor est principalement utilisé comme un
interrupteur électronique, nous utiliserons les schémas suivants représentant
un transistor soit en TTL ou MOS et une diode.

Circuits (ET, OU , NON) élaborés à partir de diodes :
Circuits (NOR, NAND , NON) élaborés à partir de transistor MOS :
Ce sont en fait la place occupée par les composants
électroniques et leur coût de production qui sont les facteurs essentiels
de choix pour la construction des opérateurs logiques de base.
Voici par exemple une autre façon de construire une circuit NOR à partir de transistor et de diodes :

Le lecteur intéressé consultera des ouvrages d'électronique
spécialisés afin d'approfondir ce domaine qui dépasse
le champ de l'informatique qui n'est qu'une simple utilisatrice de la technologie électronique en attendant mieux !
Finissons ce paragraphe, afin de bien fixer nos idées,
par un schéma montrant comment dans une puce électronique sont situés les
circuits booléens :

Supposons que la puce précédente permette de réaliser
plusieurs fonctions et contienne par exemple 4 circuits booléens : un OU,
un ET, deux NON. Voici figuré une possible implantation physique de ces 4
circuits dans la puce, ainsi que la liaison de chaque circuit booléen avec
les pattes du composant physique :

Pour information, le micro-processeur pentium IV
Northwood de la société Intel contient environ 55 000 000 (55 millions) de
tansistors, le micro-processeur 64 bits Opteron de la société concurrente
AMD plus récent que le pentium IV, contient 105 000 000 (105 millions) de
transistor.



















































