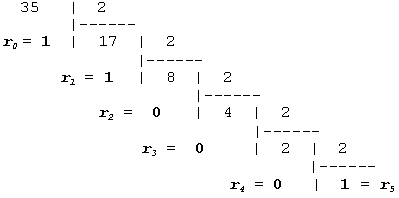-
Voyons quelles sont les nécessités
minimales pour l’écriture de documents alphanumériques simples
dans la civilisation occidentale. Nous avons besoin de :
Un alphabet de lettres minuscules
={a,b,c,...,z}
soient 26 caractères
Un alphabet de lettres majuscules
={A,B,C,...,Z}
soient 26 caractères
Des chiffres {0,1,...,9}
soient 10 caractères
Des symboles syntaxiques {? ,
; ( " ...
au minimum 10 caractères
TOTAL minimal = 72 caractères
Si l’on avait choisi un code à
6 bits le nombre de caractères codifiables aurait été
de 26 = 64 , nombre donc insuffisant pour nos besoins. Il faut
au minimum 1 bit de plus qui permet de définir ainsi 27
= 128 nombres binaires différents, autorisant le codage de 128 caractères.
-
Initialement le code ASCII est un
code à 7 bits (128 caractères) ; il a été étendu
à un code 8 bits(28
= 256 caractères) permettant le codage des caractères nationaux
(en France les caractères accentués comme : ù,à,è,é,â,...etc)
et les caractères semi-graphiques. Les pages HTML qui sont diffusées
sur le réseau Internet sont en code ASCII 8 bits.
-
Un codage récent dit " universel
" est en cours de diffusion : il s’agit du codage Unicode sur 16
bits (216 = 65536 caractères).
De nombreux autres codages existent
adaptés à diverses solution de stockage de l’information
(DCB, EBCDIC,...).
1.3 Codage des nombres entiers
: numération
Les nombres entiers peuvent être
codés comme des caractères ordinaires. Toutefois les codages
adoptés pour les données autres que numériques sont
trop lourds à manipuler dans un ordinateur. Du fait de sa constitution,
un ordinateur est plus " habile " à manipuler des nombres écrits
en numération binaire (qui est un codage particulier).
Nous allons décrire trois
modes de codage des entiers les plus connus:
Nous avons l’habitude d’écrire
nos nombres et de calculer dans le système décimal. Il s’agit
en fait d’un cas particulier de numération en base 10.
Il est possible de représenter
tous les nombres dans un système à base b (b entier, b>1).
Nous ne présenterons pas ici un cours d’arithmétique, mais
seulementles éléments nécessaires à l’écriture
dans les deux systèmes les plus utilisés en informatique
: le binaire (b=2) et l’hexadécimal(b=16).
Lorsque nous écrivons
5876 en base 10, la position des chiffres 5,8,7,6 indique la puissance
de 10 à laquelle ils sont associés :
5 est associé à
103
8 est associé à
102
7 est associé à
101
6 est associé à
100
Il en est de même dans une
base b quelconque (b=2, ou b=16). Nous conviendrons de mentionner la valeur
de la base au dessus du nombre afin de savoir quel est son type de représentation.
Soit 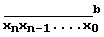 un nombre x écrit en base b avec n+1 symboles.
un nombre x écrit en base b avec n+1 symboles.
-
" xk
" est le symbole associé à la puissance " bk"
-
" xk
" Î
{0,1, ... , b-1}
Lorsque b=2 (numération
binaire)
" xk
" Î
{0,1}, les nombres binaires sont donc écrits avec des 0 et des 1,
qui sont représentés physiquement par des bits dans la machine.
Voici le schéma d’une mémoire à n+1 bits (au minimum
8 bits dans un micro-ordinateur) :
Les cases du schéma représentent
les bits, le chiffre marqué en dessous d’une case indique la puissance
de 2 à laquelle est associé ce bit (on dit aussi le rang
du bit).
Le bit de rang 0 est appelé
le bit de poids faible.
Le bit de rang n est appelé
le bit de poids fort.
1.4 Les entiers dans une
mémoire à n+1 bits : binaire
pur
Ce codage est celui dans lequel
les nombres entiers naturels sont écrits en numération
binaire (en base b=2).
Le nombre " dix " s’écrit
10 en base b=10, il s’écrit 1010 en base b=2.
Dans la mémoire il est
codé :
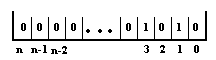 Pour une mémoire à
n+1 bits (n>1), tous les entiers naturels de l'intervalle [0 , 2n+1
-1]
seront représentés.
Pour une mémoire à
n+1 bits (n>1), tous les entiers naturels de l'intervalle [0 , 2n+1
-1]
seront représentés.
-
soit pour n+1=8 bits tous les
entiers de l'intervalle [0 , 255]
-
soit pour n+1=16 bits tous les
entiers de l'intervalle [0 , 65535]
1.5 Codage des nombres entiers
: binaire signé
Ce codage permet la représentation
des nombres entiers relatifs. Dans la représentation en binaire
signé, le bit de poids fort sert à représenter le
signe (0 pour un entier positif et 1 pour un entier négatif), les
n
autres bits représentent la valeur absolue du nombre en binaire
pur.
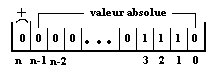 +14 est représenté
par 0000...01110
+14 est représenté
par 0000...01110
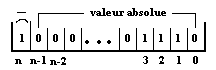 -14 est représenté
par 1000...01110
-14 est représenté
par 1000...01110
Pour une mémoire
à n+1 bits (n>1), tous les entiers naturels
de l'intervalle [-(2n
- 1),(2n -1)]seront représentés.
-
soit pour n+1=8 bits,
tous les entiers de l'intervalle [-127 , 127]
-
soit pour n+1=16 bits,
tous les entiers de l'intervalle [-32767 , 32767].
Le nombre zéro
est représenté dans cette convention (dites du zéro
positif)par : 0000...00000
Il reste malgré
tout une configuration mémoire inutilisée : 1000...00000.
Cet état binaire ne représente à priori aucun nombre
entier ni positif ni négatif de l’intervalle [-(2n -
1),(2n -1)]. Afin de ne pas perdre inutilement la configuration
"
1000...00000
", les informaticiens ont décidé que cette configuration
représente malgré tout un nombre négatif parce que
le bit de signe est 1, et en même temps la puissance du bit contenant
le "1", donc -2n.
L’intervalle de représentation
se trouve alors augmenté d’un nombre :
il devient :[-2n
,2n -1].
-
soit pour n+1=8 bits, tous les
entiers de l'intervalle [-128 , 127]
-
soit pour n+1=16 bits, tous les
entiers de l'intervalle [-32768 , 32767]
Ce codage n’est pas utilisé
tel quel, il est donné ici à titre pédagogique. En
effet le traitement spécifique du signe coûte cher en circuits
électroniques et en temps de calcul. C’est une version améliorée
qui est utilisée dans la plupart des calculateurs : elle se nomme
le complément à deux.
1.6 Un autre codage des
nombres entiers : complément à
deux
Ce codage, purement conventionnel
et très utilisé de nos jours, est dérivé du
binaire signé ; il sert à représenter en mémoire
les entiers relatifs.
Comme dans le binaire signé,
la mémoire est divisée en deux parties inégales; le
bit de poids fort représentant le signe, le reste représente
la valeur absolue avec le codage suivant :
Supposons que la mémoire
soit à n+1 bits,
soit x un entier relatif
à représenter.
- si x > 0, alors c'est
la convention en binaire signé qui s'applique (le bit de
signe vaut 0, les n bits restants codent le nombre), soit pour le nombre
+14 :
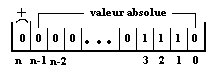 +14 est représenté
par 0000...01110
+14 est représenté
par 0000...01110
- si x < 0,
alors
-
on code |x| en binaire
signé.
-
puis l’on complémente
tous les bits de la mémoire (complément à 1 ou complément
restreint). Cette opération est un non logique effectué sur
chaque bit de la mémoire.
-
Enfin l’on additionne 1
au nombre binaire de la mémoire (addition binaire).
Exemple :soit à
représenter le nombre -14
-
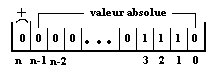 codage
de |-14|= 14
codage
de |-14|= 14
-
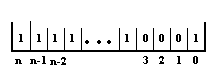 complément
à 1
complément
à 1
-
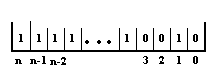 addition
de 1
addition
de 1
Le nombre -14 s'écrit
donc en complément à 2 : 1111..10010.
Un des intérêts
majeurs de ce codage est d’intégrer la soustraction dans l’opération
de codage et de ne faire effectuer que des opérations simples et
rapides (non logique, addition de 1).
2.
Numération
2.1 Opérations en
binaire
Nous avons parlé d’addition
en binaire ; comme dans le système décimal, il nous faut
connaître les tables d’addition, de multiplication, etc... afin d’effectuer
des calculs dans cette base. Heureusement en binaire, elles sont très
simples :
addition
0(1)
représente la retenue 1 à reporter.
multiplication
Exemples de
calculs :
addition
multiplication
1101101
+ 10011
_____________
10000000 |
10110
x 101
____________
10110
10110..
___________
1101110 |
Vous noterez que le procédé
est identique à celui que vous connaissez en décimal. En
hexadécimal (b=16) il en est de même. Dans ce cas les tables
d’opérateurs sont très longues à apprendre.
Etant donné que
le système classique utilisé par chacun de nous est le système
décimal, nous nous proposons de fournir d’une manière pratique
les conversions usuelles permettant de passer de la représentation
d’un nombre entre les systèmes décimal, binaire et hexadécimal.
2.2 Conversions base quelconque
<=> décimal
Voici ci-dessous un rappel
des méthodes générales permettant de convertir un
nombre en base b (b>1)en sa représentation décimale et réciproquement.
A ) Soit 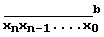 un
nombre écrit en base b.
un
nombre écrit en base b.
Pour le convertir en décimal
(base 10), il faut :
-
convertir chaque symbole
xk en son équivalent ak
en base 10, nous obtenons ainsi la suite de chiffres : an,....,a0
exemple : soit b=13,
les
symboles de la base 13 sont: {0,1,2,3,4,5,6,7,8,9,A,B,C}. Si
xk=C son équivalent
est ak=12
-
réécrire le nombre
comme une somme :
-
effectuer tous les calculs en base
10(somme, produit, puissance).

B ) Soit
" a " un nombre décimal à représenter en base
b :
La méthode utilisée
est celle de la division euclidienne.
-
Si a < b, il n'a pas besoin
d'être converti.
-
Si a >= b, on peut diviser
a par b. Et l’on divise successivement les différents quotients
qk
obtenus par la base b.
De manière générale
on aura :
a = bk.rk
+ bk-1.rk-1 + ... + b.r1
+
r0
où ri est le reste
de la division de a par b.
Cela permet, en remplaçant
chaque ri par son symbole équivalent pi
en base b, d'avoir une représentation de a dans la base
b :
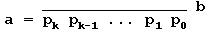
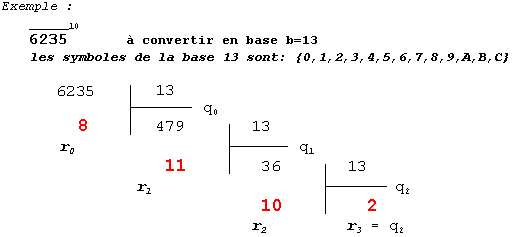
Les pi équivalents
en base 13 sont:
| r0 = 8
®
p0 = 8 |
| r1 = 11 ®
p1
= B |
| r2 = 10 ®
p2
= A |
| r3 = 2
® p3
=
2 |
Donc 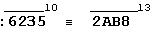
Dans les deux paragraphes
suivants nous allons expliciter des exemples de ces méthodes dans
le cas où la base est 2 (binaire).
2.3 Exemple de conversion
décimal®
binaire
Soit le nombre décimal
35
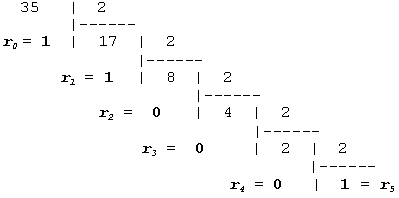
Donc : 35 (décimal) º
100011(binaire)
2.4 Exemple de conversion
binaire®décimal
Soit le nombre binaire : 1101101
sa conversion en décimal
est immédiate :
1101101 º
26 +25 +23 +23 +22
+1 =64+32+8+4+1 =109 (décimal)
Les informaticiens, pour des
raisons de commodité (manipulations minimales de symboles), préfèrent
utiliser l’hexadécimal plutôt que le binaire. L’humain, contrairement
à la machine, a quelques difficultés à opérer
sur des suites importantes de 1 et de 0. Ainsi l’hexadécimal (sa
base b=24 étant une puissance de 2) permet de diviser,
en moyenne, le nombre de symboles par un peu moins de 4 par rapport au
même nombre écrit en binaire. C’est l’unique raison pratique
qui justifie son utilisation ici.
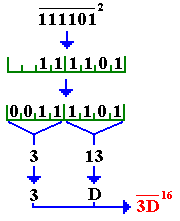
2.5 Conversion binaire®hexadécimal
Nous allons détailler
l’action de conversion en 6 étapes :
-
Soit a un nombre écrit en
base 2 (étape 1).
-
On décompose ce nombre par
tranches de 4 bits à partir du bit de poids faible (étape
2).
-
On complète la dernière
tranche (celle des bits de poids forts)par des 0 s’il y a lieu (étape
3).
-
On convertit chaque tranche en son
symbole de la base 16(étape 4).
-
On réécrit à
sa place le nouveau symbole par changements successifs de chaque groupe
de 4 bits,(étape 5).
-
Ainsi, on obtient le nombre écrit
en hexadécimal (étape 6).
Exemple :
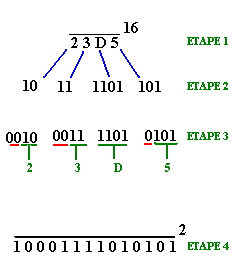
2.6 Conversion hexadécimal®binaire
Cette conversion est l’opération
inverse de la précédente. Nous allons la détailler
en 4 étapes :
-
Soit a un nombre écrit en
base 16 (ETAPE 1).
-
On convertit chaque symbole hexadécimal
en écriture binaire (nécessitant au plus 4 bits)(ETAPE
2).
-
On complète les bits de poids
fort par des 0 s'il y a lieu (ETAPE 3).
-
Le nombre " a " écrit
en binaire est obtenu en regroupant toutes les tranches de 4 bits à
partir du bit de poids faible, sous forme d’un seul nombre binaire(ETAPE
4).
Exemple :
![]() PanneauBinConv.dif\BinConv.exe
PanneauBinConv.dif\BinConv.exe
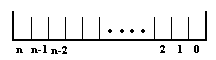
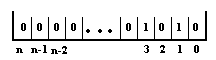
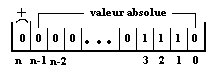
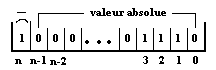
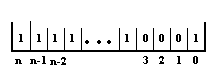 complément
à 1
complément
à 1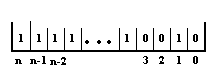 addition
de 1
addition
de 1