Chap2.2 : Les relations binaires

2.2.relations binaires

Plan du chapitre:

Rappels et conventions

1. Relation binaire sur un ensemble

2. Produit de relations binaires

3. Représentation matricielle d’une relation binaire

4. Relation binaire transposée

5. Matrice du produit de deux relations

6. Fermeture transitive d’une relation binaire

7. Fermeture réflexo-transitive d’une relation binaire

8. Algorithmes de calcul de matrices

9. Exemple de calcul sur une généalogie

Un peu de mathématiques utiles, mais pas trop !

Rappels et conventions

En informatique, la notion de relation est importante. Nous indiquons ici sans rentrer dans les détails que le lecteur trouvera dans des livres spécialisés, en particulier sur la recherche opérationnelle, comment on implante une relation binaire à travers sa matrice de représentation.

Ceci peut donc être considéré comme un bon exemple d’application des matrices booléennes en informatique.

Convention

Lorsque nous écrivons " x ¬ a " ceci se lit: "x vaut la valeur de a".

1. Relation binaire sur un ensemble

Nous appelons relation binaire sur un ensemble E non vide, tout sous-ensemble R du produit cartésien E x E.

R Ì E x E

Il est donc possible de définir l’union et l’intersection de deux relations binaires.

2. Produit de relations binaires

Soient r et s deux relations binaires sur un ensemble non vide E. On définit le produit p = r.s ainsi :

" a , a Î E
" b , b Î E a r.s b ssi $ c , c Î E / (a r c) et (c s b)

Nous énonçons brièvement quelques propriétés de ce produit :

Le produit est associatif.
Le produit n’est pas commutatif.

Notations

rⁿ = r. r.... r (n fois)

r^0
,^{est la relation
telle que :}
" a , a Î E on a toujours a r⁰ a

r^n+m= rⁿ . r^m

3. Représentation matricielle d’une relation binaire

Cas où E est un ensemble fini, c’est d’ailleurs le seul cas qui nous intéresse en informatique où nous ne pouvons pas traiter du non fini.

Soit E l’ensemble : E = {a₁,a₂,...,a_n}
Soit r une relation binaire sur E.
Soit M une matrice carrée d’ordre n sur {0,1}. Nous notons ((m_i,j)) l’élément générique de la matrice M.

Nous dirons que M est la matrice de représentation de la relation binaire r et nous la noterons Mr, ssi par définition :

si a_i r a_j alors m_i,j ¬ 1 sinon m_i,j ¬ 0 fsi

Exemple :

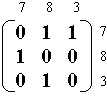
E = { 7,8,3 } ; r = { (7,8),(7,3),(3,8),(8,7) }

a₁ = 7 ; a₂ = 8 ; a₃ = 3

Voici la matrice Mr de la relation r définie ci-haut :

Mr =

4. Relation binaire transposée

Soit E l’ensemble : E = {a₁,a₂,...,a_n}
Soit r une relation binaire sur E.

Nous notons r^t la relation binaire telle que :

" a , a Î E
" b , b Î E

a r^t b ssi b r a

Par construction la matrice de r^t est la transposée de la matrice de r.

M r^t = ^t Mr

5. Matrice du produit de deux relations

En munissant l’ensemble {0,1} d’une structure d’algèbre de boole avec les opérateurs Ù , Ú ,Ø , il nous est possible d’effectuer des calculs sur les matrices de représentation de relations binaires.

Soient r et s deux relations binaires sur un ensemble non vide E. Soit le produit p = r.s, Mr , Ms et Mp les matrices de r, s et p.
Soit ((a_i,j)) l’élément générique de Mr.
Soit ((b_i,j)) l’élément générique de Ms.

La matrice Mp = Mr.s est très exactement par définition le produit booléen en croix des matrices Mr et Ms.

Mr x Ms = Mp = Mr.s = [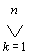 (a_i,kÙ b_k,j)]

6. Fermeture transitive d’une relation binaire

Soit E l’ensemble : E = {a₁,a₂,...,a_n}
Soit r une relation binaire sur E.

Nous posons par définition sa fermeture transitive qui est la relation binaire r+ :

r+ = 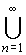rⁿ^{, en fait dans le cas où E est fini l’union se limite à un
nombre fini k de}rⁿ^{distincts donc :}

r+ = 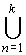rⁿ

7. Fermeture réflexo-transitive d’une relation binaire

Soit E l’ensemble : E = {a₁,a₂,...,a_n}
Soit r une relation binaire sur E, sa fermeture transitive r+ .

On note par définition r* sa fermeture réflexo-transitive :

r^* = r+ È r⁰

Remarque

Soit un couple (a,b) de E x E tel que a r^* b :
a r^* b Û $ n , n Î E / a rⁿ b

^{Nous dirons dans ce cas qu’il
existe " un chemin de longueur n, allant de a vers b ". En effet d’après
la définition du produit :}

a r^* b Û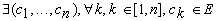
^{tels
que : ( a r
c₁)
et (c₁
r c₂)
...et
(c_nr
b
)}

8. Algorithmes de calcul de matrices

FermetureTrans.dif \Ftrans.exe

Calcul de la matrice produit à partir de la formule :

Mr x Ms = Mp = Mr.s = [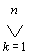(a_i,kÙ b_k,j)]

Notons ((m_i,j)) l’élément générique de la matrice produit.

Corps d’un algorithme de calcul :

pour i ¬ 1 jusquà n faire
pour j ¬ 1 jusquà n faire
S ¬ 0 ;
pour k ¬ 1 jusquà n faire
S ¬ S Ú (a_i,kÙ b_k,j)
Fpour ;
m_i,j ¬ S
Fpour
Fpour

Algorithme de Warshall pour la fermeture transitive :

Avec les mêmes notations soit((a_i,j)) l’élément générique de la matrice Mr, l’algorithme de Warshall calcule Mr⁺ :

pour k ¬ 1 jusquà n faire
pour i ¬ 1 jusquà n faire
pour j ¬ 1 jusquà n faire
a_i,j¬ a_i,jÚ (a_i,kÙ a_k,j)
Fpour ;
Fpour
Fpour

9. Exemple de calcul sur une généalogie

E = l’ensemble des individus d’une même famille depuis plusieurs générations.

Soient r, s et t les relations binaires :

x r y ssi x est le père de y
x s y ssi x est la mère de y
x t y ssi x est un enfant de y

On peut définir les liens familiaux à l’aide des opérations sur les relations binaires.

r² = est grand père paternel de
s² = est grand mère maternelle de
r.s = est grand père maternel de
s.r = est grand mère paternelle de(non commutativité évidente !)
r È s = est parent de
rⁿ = est arrière arrière...arrière grand père paternel de
(r È s)⁺ = est un ancêtre de (on voit ici la signification pratique de la fermeture transitive qui relie deux individus par un chemin d’ascendants dans son arbre généalogique)
u.u^t = est frère ou sœur de etc ....