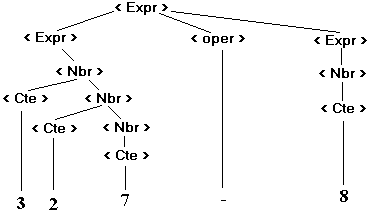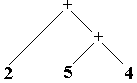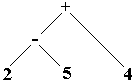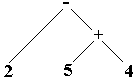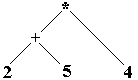2.3.théorie des langages


Plan du chapitre:

1. Notations et définitions générales
 

2. Grammaire formelle ou algébrique

     
    2.1 Monoïde
    2.2 Grammaire formelle
    2.3 Opérations sur les mots
    2.4 Langage engendré par une grammaire
    2.5 Grammaire d’états finis
    2.6 Arbre de dérivation d’un mot
    2.7 Diagrammes syntaxiques


3. Classification de Chomsky des grammaires
 

    3.1 Les grammaires syntaxiques
    3.2 Les grammaires sensibles au contexte
    3.3 Les grammaires indépendantes du contexte
    3.4 Les grammaires d’états finis ou de Kleene


4. Applications et exemples

     
    4.1 Expressions arithmétiques : une grammaire ambiguë
    4.2 Expressions arithmétiques : une grammaire non ambiguë


Un langage est fait pour communiquer. Les humains doivent communiquer avec les ordinateurs : ils ont donc élaboré les bases d’une théorie des langages. Dans ce chapitre nous donnons les fondements formalisés d’une telle théorie autour de la notion de grammaire formelle.
 

1. Notations et définitions générales

  
Remarque et convention :
  • Certains éléments d’un langage s’appellent les symboles.
  • Soit S un ensemble de symboles(S ¹ Æ). ce sont les éléments indécomposables dans ce langage (c’est-à-dire non exprimables en autres symboles du langage).

 

Définition expression sur S
On appelle expression sur S, toute suite finie de symboles de S.

e : [1,n]®S (e est alors un métasymbole décrivant l’expression S).
e est une expression sur S, n est un entier naturel, n ³ 1.

Notation:
On désigne e par : e = s1s2s3...sn , n ³ 1 où : "k, 1£ k £ n , sk ÎS
et 
par définition e(k) = sk  ("k, k Î[1,n] )    On note S+ = { e / e expression sur S } 
   S+ est l'ensemble de toutes les expressions formées sur S.

Deux opérations sur S+ :

égalité d’expressions
Soient e1 et e2 deux expressions sur S, on définit leur égalité ainsi :
 
e1 = e2  ssi    $k , k ³ 1 
   e1 : [1,k]®S
   e2 : [1,k]®S
   "i,1 £ i £ k
   e1(i) = e2(i)

concaténation d’expressions
soient eÎS+ et f Î S+,
on construit le "produit" des deux expressions e.f :
 
e : [1,n]®S
f : [1,p]®S
e.f: [1,n+p]®S		   avec :
  e.f(i) = e(i) ssi i Î[1,n]
  e.f(i) = f(i) ssi i Î [n+1,n+p]

Notation : (la concaténation de 2 expressions)
e = s1s2s3...sn 
f = t1t2t3...tp		  e.f est notée : 
 s1s2s3...snt1t2t3...tp

 

2. Grammaire formelle ou algébrique
     
    Comme dans les langages naturels, les informaticiens ont, grâce aux travaux de N.Chomsky, formalisé la notion de grammaire d’un langage informatique.
     
     

    2.1 Monoïde

A) Soit A un ensemble fini appelé alphabet ainsi  défini:
  A = { a1 ,..., an } ( A ¹ Æ ) Notations :
A1 = A
A2 = { x1x2 / (x1ÎA) et (x2ÎA) }
A3 = { x1x2x3 / (x1ÎA) et (x2Î A) et (x3 ÎA)} 
..........

An = { x1x2....xn /  " i , 1 £ i £ n , (xi ÎA) } 
 

convention
A0 = { e } (appelé séquence vide)

On définit sur 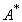 une loi de composition interne appelée concaténation, notée ·  :
 
( x, y ) ¾® x · y = xy (noms des symboles accolés)

la concaténation possède les propriétés suivantes :
 
  • elle est associative : 
      • (x · y) · z = x · (y · z)
  • l’élément e est un élément neutre : 
      • " x Î A* , x · e = e · x = x

 
Définition : ( A*, · ) est un monoïde libre

 


2.2 Grammaire formelle
       
    2.3 Opérations sur les mots
       
    Soit G une C-Grammaire, G = (VN,VT,S,R). On définit sur ( VN È VT )* une relation binaire appelée " dérivation directe " notée Þ définie comme suit :
     

    Définition : dérivation directe
    Soient a Î ( VN È  VT )* et b Î ( VN È VT )*

    On note a Þ b et l’on dit que b dérive directement de a, 
    ou que a se dérive directement en b.

    ssi
     
    $a Î ( VNÈ VT )* 
    $b Î ( VNÈ VT )* 
    $ ri Î R,telle que: 
            ri : Ai¾®g    		      a et b s'écrivent :

           a = a Aib
           b = a gb

    Notation :
    On emploie aussi les termes de " règle de réécriture "
    ou de " règle de dérivation ".

    Nous obtenons un processus de construction des mots de la grammaire G par application de la dérivation directe. Si l’on réitère plusieurs fois ce processus de dérivation directe, on obtient à partir d’un mot, une suite de mots de G. En fait il s’agit de construire la fermeture transitive de la relation binaire Þ . Cette nouvelle relation est appelée la dérivation dans G (la dérivation directe en devenant un cas particulier)
     

    Définition : dérivation
    On dit que x se dérive en y, s’il existe une suite finie de dérivations directes permettant de passer de x à y :

    (x,x0,x1,...,xn et y) étant des mots de ( VNÈ VT )* on a le chemin suivant :

    x Þ x0 Þ x1 Þ.... xn Þy

    on écrit : x Þ*y , et l’on lit : x se dérive en y.

     

    2.4 Langage engendré par une grammaire

    On s’intéresse maintenant à toutes les dérivations possibles construites dans G, par application des règles de G, en privilégiant un point de départ unique pour chacune des dérivations. Nous avons vu que chaque règle de G commençait en partie gauche par un élément de VN. Nous construisons alors toutes les productions ayant comme point de départ S l’axiome de G. L’ensemble L de tous les mots construits s’appelle le " langage engendré par G " : L Ì  VT*.

    Définition : langage engendré
    Soit la C-grammaire G, G = ( VN , VT , S , R )

    L’ensemble L(G) = { u Î VT* / S Þ* u } 
    s'appelle le langage engendré par G.

    Exemple :
    G0 : VN = { S } le langage engendré par G0 est
    VT = {a,b} L(G0) = { anbn / n ³ 1 }
    Axiome : S

    Règles
        1 :  S ¾®aSb
        2 :  S ¾® ab
     
     

    2.5 Grammaire d’états finis

    Ce sont des C-Grammaires dans lesquelles les parties droites de règles ont une forme particulièrement simple (on classifie d’ailleurs les grammaires algébriques en général en 4 types en fonction de la forme de leurs règles. Les C-grammaires sont dites de type-2 et les K-grammaires ou grammaires de Kleene sont dites de type-3).

    Pour une grammaire de type-3 ou K-grammaire les règles sont de 2 formes :
     
    A ¾® a    ( a Î VT)
     ou bien
    A ¾® aB    ( B Î VN et B pouvant être égal à A )

    Exemple :

    G1 : VN = { S,A}
    VT = {a,b}
    Axiome : S
    Règles
               1 :   S ¾® a S
        2: S ¾® aA
        3: A¾® bA
        4: A¾®b
    Le langage engendré par G1 est : L(G1) = { anbp / (n ³ 1) et (p ³ 1) }
     
     

    2.6 Arbre de dérivation d’un mot

    Notion d’arbre :

    On appelle arbre A toute structure sur un ensemble E qui est :
    • soit une structure vide notée A,
    • soit une élément noeud r associé à un nombre fini d’arbres disjointsA1,A2,...,An.
    • A = < r,A1,A2 ,...,An>

    Représentation graphique d’un arbre :

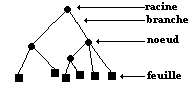
    Un arbre est dit " étiqueté " si l’on nomme (attribution d’un symbole de nom) sa racine et ses noeuds.
     

    Définition : arbre de dérivation
    Soit la C-grammaire G, G = ( VN, VT, S, R ).
    Un arbre étiqueté est un " arbre de dérivation " dans G ssi :
    • L’alphabet des étiquettes est inclus dans VN È VT.
    • Les noeuds sont étiquetés par des éléments de VN.
    • Les feuilles sont étiquetées par des éléments de VT.
    • L’étiquette de tout noeud est un élément de VN.
    • Pour tout noeud < A,f1,f2,...,fn> on associe une règle R 
           de la forme : A¾®f1f2...fn
           (règle de dérivation dans G).

    Exemples :

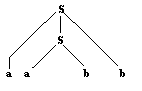
    mot a2b2 dans G0    		 Règles de G0 appliquées : 

       S  ¾®1  aSb  ¾® 2  aabb 

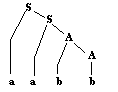
    mot a2b2 dans G1    		 Règles de G1 appliquées : 

       S  ¾®1  aS  ¾® 2  aaA ¾® 3  aabA  ¾® 4  aabb

    Définition : grammaire ambigüe
    Une grammaire est dite ambiguë si une chaîne a au moins deux arbres de dérivation différents dans G.

    Exemple de grammaire ambiguë :
    G2 : VN = {S}
    VT = {( , )}
    Axiome : S
    Règles
            1  : S ¾® (SS)S
       2 : S ¾®  e

    Le langage L(G2) se dénomme langage des parenthèses bien formées.

    Soit le mot (( )) de G2 , voici 2 arbres de dérivation de (( )) dans G2 :
     
    Arbre 1 :
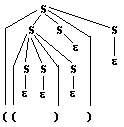    		Arbre 2 :

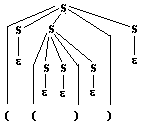    - Arbre 1 correspond dans G2 à la suite des dérivations suivantes :
    (afin d’y voir plus clair entre les S choisis nous allons colorier les symboles S)

    on part de l’axiome S et l’on applique la règle 1:

        S ¾®1 ( SS ) S

    on applique la règle 1 au premier S de gauche :

    S ¾®1( SS ) S
     

    Ce qui donne :

      S ¾®1( SS ) S ¾®1( (S S) SS ) S

    puis on dérive tous les symboles S à partir de la règle 2 :
     
    S ¾®  e
    S ¾®  e
    S ¾®  e
    S ¾®  e
    S ¾®  e

     
    S ¾® ... ¾®2(( e  e)e  e ) e

    comme xe  = ex = x  ,  nous avons donc : ((e e ) e e ) e = (()) ,
     

    - Arbre 2 correspond dans G2 à la suite des dérivations suivante :
    S  ¾®1   (  S  S )  S ¾®1(S ( S S ) S) S ¾®2 ... ¾®2(e (e e) e) e = (()).
     

En conclusion, le mot (()) dérive de l'axiome S :
 
  S Þ * (( ))

 
 

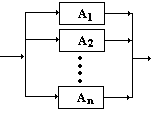
2.7 Diagrammes syntaxiques

Il est possible de représenter graphiquement les règles de dérivation d’une grammaire formelle par des diagrammes dénotés " diagrammes syntaxiques ". Cette représentation a pour effet de condenser l’écriture des règles et d’autoriser une meilleure lisibilité.
 
 
 
REGLES DIAGRAMMES
  A ÎVN
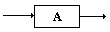
  a ÎVT
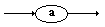
     B ¾® e
   B ¾® A1
   B ¾® A2          ou encore :
   .....                   B ¾® A1|...|An
   B ¾® An
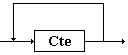
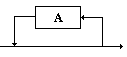
   B ¾® AB | e
      ou : 
   B ¾® {A}*
   B ¾® AB | A
      ou: 
   B ¾® {A}+

     
     

    3. Classification de Chomsky des grammaires
     

    Traditionnellement les grammaires algébriques sont classables en quatre catégories qui se différentient par la forme de leurs règles. Elles sont notées par leur type (type 0, type 1, type 2, type 3). Il y a une relation d’inclusivité provenant de leurs définitions :

    type 3 Ì type 2 Ì type 1 Ì type 0
     
     

    3.1 Les grammaires syntaxiques - type 0

    Les règles ont une forme générale : a ¾® b
     
    pour une règle a ¾® b ,les symboles (a, b) doivent être de la forme :
    a Î ( VN È  VT )+
    b Î ( VN È VT )*

     

    3.2 Les grammaires sensibles au contexte - type 1

    Les règles ont la forme suivante : aAb¾®agb
     
    pour une règle aAb ¾® agb,les symboles(a, b, g, A) doivent être de la forme :
    A Î VN
    a Î ( VN È VT )*
    b Î ( VN È VT )*
    g Î ( VN È VT )+
     

     
     

    3.3 Les grammaires indépendantes du contexte - type 2

    Les règles ont la forme suivante : A ¾® a
     
    Pour une règle A ¾® a,les symboles(a,A) doivent être de la forme :
    a Î ( VN È  VT )*
    A Î VN

     

    3.4 Les grammaires d’états finis ou de Kleene - type 3

    Les règles n’ont que deux formes possibles :

    A ¾® a
      ou bien
    A ¾® aB
     
    Pour ces règles, les symboles(a,A, B) doivent être de la forme :
    A Î VN
    B Î VN
    a Î VT

     
     
     

    4. Applications et exemples
     

    une phrase simple.

    Les identificateurs en pascal.
     
     

    4.1 Expressions arithmétiques : une grammaire ambiguë

       
    Gexp = (VN,VT,Axiome,Règles)

    VT = { 0, ..., 9, +,-, /, *, ), (}
    VN = { á  Expr ñ, á  Nbr ñ, á  Cte ñ, á  Oper ñ}
    Axiome : á  Expr ñ
    Règles :
    1 :á  Expr ñ ¾® á  Nbr ñ | (á Expr ñ ) | á  Expr ñ á Oper ñ  á Expr ñ
    2 :á  Nbr ñ ¾® á  Cte ñ | á  Cte ñ á  Nbr ñ
    3 :á  Cte ñ ¾® 0 | 1 |...| 9
    4 :á  Oper ñ ¾® + | - | * | /
     

    Les mots de L(Gexp) sont des expressions de la forme (x+y-z)*x etc... où x, y, z sont des entiers.
     

    Exemple : 327 - 8 est un mot de L(Gexp)

    Il n’a qu’un seul arbre de dérivation dans Gexp dessinons son arbre de dérivation :


     

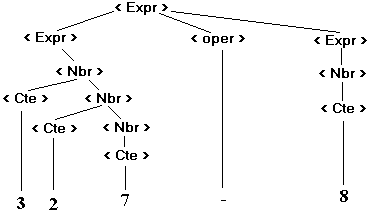
    Nous pouvons faire ressortir les liens abstraits qui relient les trois éléments terminaux 327, - et 8 :


     

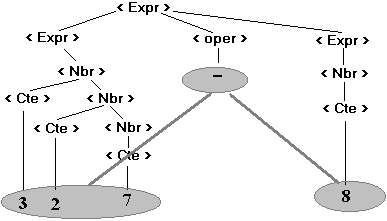
    L’arbre obtenu en grisé à partir de l’arbre de dérivation s’appelle l’arbre abstrait du mot " 327-8 ".

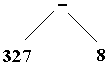
    Cet arbre abstrait permet de manipuler la structure générale du mot facilement tout en résumant la structure générale de l’arbre de dérivation.
     

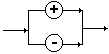
    Soientt trois autres mots de L(Gexp) 2+5+4, 2-5+4, 2+5*4, ils ont chacun deux arbres de dérivation. Nous donnons ci-après deux arbres abstraits de chaque mot.
     
    Arbre-1 : 2+5+4
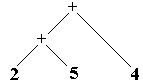    		Arbre-2 : 2+5+4
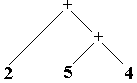    Arbre-3 : 2-5+4
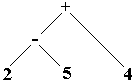    		Arbre-4 : 2-5+4
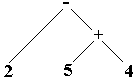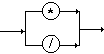
    Arbre-5 : 2+5*4
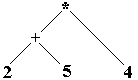    		Arbre-6 : 2+5*4

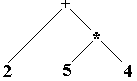    Nous remarquons donc que Gexp est une grammaire ambiguë puisqu’il existe un mot possédant au moins deux arbres de dérivation. Pour l’instant ce ne sont que des concaténations de symboles sans aucun sens.

    Si nous voulions aller plus loin en donnant un sens (de la sémantique) à ces mots de telle façon qu’ils représentent des calculs sur les entiers avec les propriétés classiques des opérations sur les entiers, nous pourrions nous trouver un " bon choix " parmi les arbres abstraits précédents. Nous appellerons ces choix " interpréter " l’expression.

    Examen de la situation pour le mot 2+5+4:


    L’opérateur " + " est associatif donc pour notre interprétation les deux arbres 1 et 2 peuvent convenir.
     

    Examen de la situation pour le mot 2-5+4:


    Les opérateurs + et - sont de même priorité et nous obtenons deux expressions différentes selon le choix de l’arbre.

    Traditionnellement lorsque deux opérateurs ont la même priorité, l’évaluation se fait à partir de la gauche de l’expression. Donc l’arbre 3 conviendrait.

    Nous pourrions penser lever l’ambiguïté en choisissant systématiquement l’arbre abstrait d’évaluation à gauche correspondant à un parenthésage implicite à gauche(comme arbre-1 et arbre-3) :

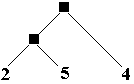
    Nous allons voir ci-dessous que ce n’est pas possible.

    Examen de la situation pour le mot 2+5*4:


    Les opérateurs + et * n’ont pas la même priorité. Nous obtenons deux expressions différentes selon le choix de l’arbre. Mais ici c’est le choix de l’arbre 6 qui s’impose à cause de la priorité du * sur le +.

    Nous avons fait ressortir le fait qu’il était impossible de privilégier systématiquement pour " l’interprétation " des expressions une catégorie d’arbre plutôt qu’une autre, il faut donc changer de grammaire et éviter l’ambiguïté.
     
     

       
    4.2 Expressions arithmétiques : une grammaire non ambiguë
 
Nous donnons ci-dessous une grammaire non ambiguë basée sur la précédente et tenant compte de la précédence (priorité d’opérateur). Nous séparons les opérateurs en deux catégories ; les opérateurs de priorité zéro (Oper_0) et ceux de priorité un (Oper_1).

facteur

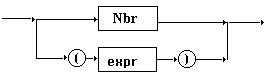
expr

 

terme

 
 
 
Nbr
Oper_0
Oper_1

Cte

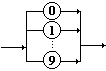
Axiome : áexprñ
 

En pratique ce ne sera pas une telle grammaire qui sera retenue pour le calcul des expressions arithmétiques car elle contient une règle récursive gauche, ce qui la rend difficilement analysable par des procédés simples.