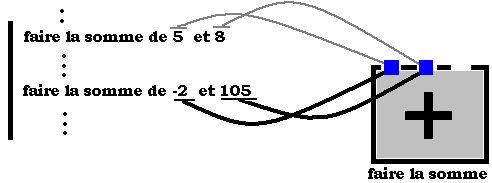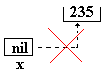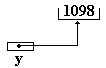2.4.une grammaire du Pascal
Plan
du chapitre:
1. Rappel de la structure d’un programme Pascal
2. Les opérateurs en pascal
2.1 Les opérateurs multiplicatifs
2.2 Les opérateurs additifs
2.3 Les opérateurs relationnels
2.4 Déclarations des constantes
3. Déclarations des types en Pascal
3.1 Déclarations des types
simples
3.2 Déclarations des types
structurés
4. Instructions en Pascal
4.1 Instruction d'affectation
4.2 Instruction de
condition
4.3 Instruction d'itération while…do
4.4 Instruction
d'itération repeat…until
4.5 Instruction d'itération for…do
4.6 Instruction case…of
5. Fonctions et procédures en Pascal
6. Paramètres en Pascal
6.1 Lecture seulement
6.2 Accès direct
7. Fonction ou procédure ?
8. Visibilités des variables
9. Variables dynamiques ou pointeurs
10. Récursivité en programmation
Il ne s'agit pas d'apprendre
systématiquement toutes les subtilités du langage pascal,
mais plutôt d'un résumé consistant mais suffisant, visant
à se aqcuérir les principes de base du langage relativement
à la programmation.
Le lecteur tirerait avantage
à récupérer un polycopié en ligne d'un cours
de pascal (taper pascal sur un moteur de recherche du web ou bien aller à
http://www.developpez.com rubrique pascal-delphi) pour se étudier
complètement le langage. La société Borland-Inprise
met sur son site web, gratuitement par téléchargement, des compilateurs
pascal anciens mais efficaces pour le débutant (http://www.borland.fr).
 PanneauPascalAlgo.dif
PanneauPascalAlgo.dif
1. Rappel de la structure d’un programme
Pascal
Nous allons utiliser une description
d’un Pascal réduit à l’aide des diagrammes syntaxiques.
Un programme Pascal est composé
de la façon suivante :
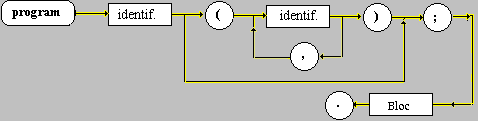
- Soit donc d'une partie
en-tête ( nom , paramètres ) :

- d'une partie corps (ou Bloc)
:

- et se termine par un point
:

Exemples d'en-tête
:
1°) program exemple_01
( input, output ) ;
2°) program exemple_02
;
Le langage Pascal étant
structuré, un bloc est composé de sections ou paragraphes bien
séparés :
- les étiquettes ou
label,
- les constantes ou const,
- les types ou type,
- les variables ou var,
- les fonctions et les procédures,
- les instructions exécutables.
Un Bloc Pascal:

En pratique un bloc Pascal contient deux parties : des déclarations
et des instructions
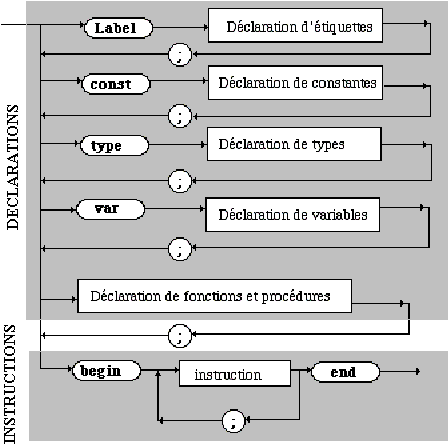
Exemple de programme avec Bloc :
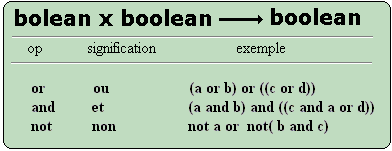
2. Les opérateurs en pascal
Liste de tous les opérateurs
en Pascal.
Ce sont les règles
de composition qui précisent la priorité retenue entre les
différents opérateurs du langage. Ces priorités sont
réparties en 4 niveaux :
- plus haut niveau de priorité
4 : opérateur unaire not
- niveau de priorité
3 : opérateurs multiplicatifs
- niveau de priorité
2 : opérateurs additifs
- plus bas niveau de priorité
1 : opérateurs relationnels
2.1 Les opérateurs
multiplicatifs
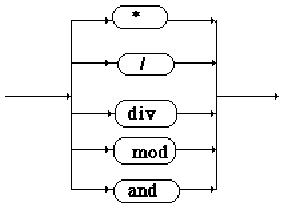
| Opérateur |
Types des opérandes |
Type du résultat |
| *
multiplication |
real ou integer |
real ou integer |
| *
intersection |
Ens=set of T0 |
Ens=set of T0 |
| /
division |
real ou integer |
real |
| div
quotient euclidien |
integer |
integer |
| mod
reste euclidien |
integer |
integer |
| and
et logique |
boolean |
boolean |
2.2 Les opérateurs
additifs
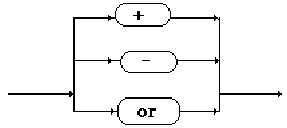
| Opérateur |
Types des opérandes |
Type du résultat |
| +
addition |
real ou integer |
real ou integer |
| +
union |
Ens=set of T0 |
Ens=set of T0 |
| -
soustraction |
real ou integer |
real ou integer |
| -
différence |
Ens=set of T0 |
Ens=set of T0 |
| or
ou logique |
boolean |
boolean |
ATTENTION :
| Lorsqu'ils sont unaires
les opérateurs "+" et "-" indiquent le signe de la variable. |
2.3 Les opérateurs
relationnels
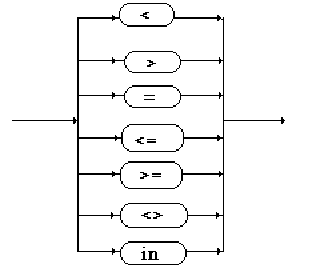
| Opérateur |
Types des opérandes |
Type du résultat |
| <
inférieur strict |
type scalaire |
boolean |
| >
supérieur strict |
type scalaire |
boolean |
| <=
inférieur ou égal |
type scalaire |
boolean |
| <=
inclusion large |
Ens=set of T0 |
boolean |
| =
égal |
type scalaire |
boolean |
| =
égal |
type pointeur |
boolean |
| =
égal |
Ens=set of T0 |
boolean |
| >=
supérieur ou égal |
type scalaire |
boolean |
| >=
contient large |
Ens=set of T0 |
boolean |
| <>
différent |
type scalaire |
boolean |
| <>
différent |
type pointeur |
boolean |
| <>
différent |
Ens=set of T0 |
boolean |
| in
appartient |
Ens=set of T0 |
boolean |
| in
appartient |
type intervalle |
boolean |
Liste de tous les opérateurs selon le type de données
en Pascal :
|
opérateurs sur les entiers
|
opérateurs sur les réels
|

opérateurs sur les ensembles : set of
|
|
opérateurs sur les booléens
|
opérateurs de comparaison sur
un type T
|
2.4 Déclarations des
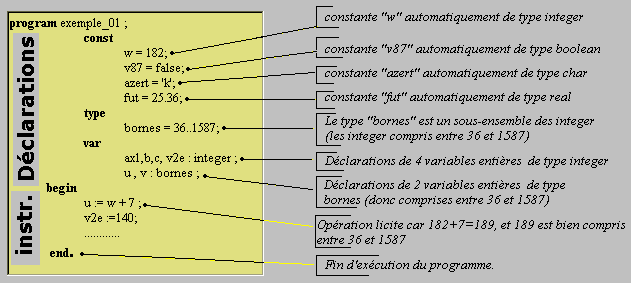
constantes
Sert à associer un identificateur
à une valeur de constante, non modifiable dans le reste du programme.

Exemple :
program exemple_03 ;
const
x=12; <------------
constante de type integer.
a2=true;
<------------ constante de type boolean.
y='h'; <------------
constante de type char.
r2=25.36;
<------------ constante de type real.
.
.
.
Il existe 3 identificateurs
de constantes prédéfinis : True , False , et
Nil .
3. Déclarations des types en Pascal
Les types sont utilisés
pour créer de nouveaux domaines de définition de variables.
Une déclaration d'un nouveau type de données sert associer un identificateur à
un type de données, construit par l'utilisateur. Cette construction
élaborée à l'aide de constructeur de type détermine
l'ensemble des valeurs possibles des variables de ce nouveau type.
On classe les types en 3 catégories
:
Type
< déclaration
de type >
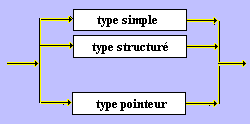
3.1 Déclarations des
types simples
Cette déclaration est
composée des :
- type scalaire
- type intervalle
- identificateur d'un type
déjà déclaré
A) Type simple :
< Type simple >
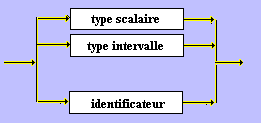
B) Types simples / Les types
scalaires ( 2 sortes ) :
Les types prédéfinis
:
- integer
- real
- char
- boolean
Les types énumérés
:
identif0 = ( identif1,identif2,....,identifk
)
Il s'agit ici d'une définition
en extension des éléments du type. Les identifn sont des constantes
symboliques du type et doivent être tous différents dans la
même énumération, et ne peuvent se retrouver ni dans
une autre énumération, ni redéfinis ailleurs.
| Ce type est doté d'une
fonction spécifique : ord qui dénote le numéro
d'ordre d'un élément dans l'ensemble des valeurs du type (attention
l'ordre est construit de gauche à droite et la numérotation
débute à la valeur 0). |
Exemple :
Type
jour = (lundi,
mardi, mercredi, jeudi, vendredi, samedi, dimanche ) ;
| lundi |
mardi |
mercredi |
jeudi |
vendredi |
samedi |
dimanche |
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
Ainsi :
ord(jeudi) = 3
ord( lundi) = 0
REMARQUE
:
| Les types scalaires sauf
le type real bénéficient de 2 fonctions succ et pred
succ : T ----->
T / succ (ai) = ai+1 (successeur dans T , lorsqu'il existe)
pred : T ----->
T / pred (ai) = ai-1 (prédécesseur dans T, lorsqu'il
existe )
|
C) Types simples / Les types
intervalles :

Il peut être défini
comme un intervalle fermé borné d'un autre type scalaire, sauf
real.
Exemples :
Type
jour = (lundi
, mardi , mercredi , jeudi , vendredi , samedi , dimanche ) ;
mois = 1..12
;
week_end
= vendredi..dimanche ;
lettre_min
= 'a'..'z' ;
lettre_maj
= 'A'..'Z' ;
3.2 Déclarations des
types structurés
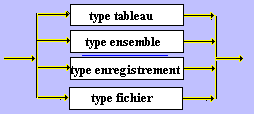
Une définition de type structuré, précise
par l'intermédiaire du constructeur de type, la méthode de
structuration et le type de ses composants.
Type
structuré / Tableau :
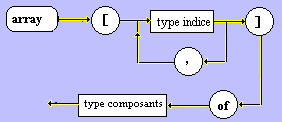
Le type tableau est défini
par le constructeur de type array[ ] of. C'est une structure homogène,
formée d'un nombre fixe de composants qui sont tous du même
type de base. Tous les composants d'un tableau sont désignés
par des indices, qui sont des expressions appartenant au type indice
du tableau.
| Un tableau est en fait une
structure de donnée à accès aléatoire ,
c'est à dire que tous ses composants peuvent être sélectionnés
et atteints de manière égale. Ils sont rangés dans l'ordre
des indices. |
Un tableau à n dimensions
(un vecteur est représenté par un tableau à une dimension,
une matrice par un tableau à deux dimensions...) est défini
par n types d'indices séparés par des virgules.
| Un type indice est
un type simple sauf real et integer. |
Exemple :
Type
jour = (lundi,
mardi, mercredi, jeudi, vendredi, samedi, dimanche ) ;
mois = 1..12
;
week_end =
vendredi..dimanche ;
lettre_min
= 'a'..'z' ;
lettre_maj
= 'A'..'Z' ;
tableau_01
= array[jour] of mois;
tableau_02
= array[jour] of array[1..30] of mois;
tableau_03
= array[jour,1..30] of mois;
tableau_04
= array[lettr_min,0..5,jour,boolean] of char;
var
T1 : tableau_01;
T2 : tableau_02;
T3 : tableau_03;
T4 : tableau_04;
etc.....
ATTENTION:
| Notons ici que malgré
la similitude de construction des deux types tableau_02 et tableau_03 (ce
sont des types de matrices où l'indice ligne varie dans le type jour,
et l'indice colonne varie dans le type 1..30), ce ne sont pas des types
identiques, car ils sont déclarés séparément.
Donc dans l'exemple précédent,
T2 et T3 ne sont pas des tableaux du même type.
|
Accès
aux variables d'un type tableau
Il faut, afin de pouvoir accéder
à un composant d'un tableau, utiliser des indices obligatoirement
de même type et en même nombre qu'indiqués dans la déclaration.
Exemple : (en reprenant les
déclarations précédentes)
var
T1 : tableau_01;
T2 : tableau_02;
T3 : tableau_03;
T4 : tableau_04;
m : mois;
j : jour;
k : 1..30;
L,b: boolean;
n : integer;
c : lettre_min;
Les écritures
suivantes sont licites :
j:= jeudi; k:= 20; c:='f'; L:=false;
b:=true; n:=2;
T1[mardi]:= 8; T1[j]:= 10;
T2[mardi,5]:= 8; T2[mardi] [5]:=
8; T2[j,k-3]:= 8; T2[j] [k-3]:= 8;
T3[mardi,5]:= 8; T3[mardi] [5]:=
8; T3[j,k]:= 8; T3[j] [k]:= 8;
T4['t',3,samedi,true]:= 'h'; T4['t'][3][samedi][true]:=
'h';
T4[c,n+2,j,L or b]:= '+';
...... etc
Type
structuré / Ensemble :

Un type ensemble est défini
d'un manière extensive par le constructeur set of, le domaine
des valeurs de ses éléments par son type de base.
| le type composant
est un type simple sauf real et integer. |
C'est un ensemble fini et l'on
peut construire tous ses sous-ensembles :
Exemple :
Type
couleur = (noir,blanc);
ens_couleur
= set of couleur;
var
x,y,z,t : ens_couleur;
begin
x := [ ]
; <--- ensemble vide (0 élément)
y := [noir];
<--- ensemble (1 élément)
z := [blanc];
<--- ensemble (1 élément)
t := [noir,blanc];
<--- ensemble (2 éléments : maximum
possible de l'exemple)
etc.....
On peut dire en fait que le type
ens_couleur est l'ensemble P(couleur) (ensemble des parties) et que toute variable
du type ens_couleur est un sous-ensemble de P(couleur).
Type structuré / Enregistrement :
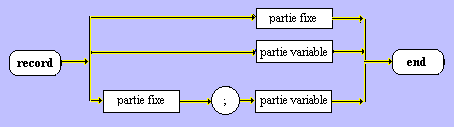
Le type enregistrement est une
collection de composants appelés champs de l'enregistrement.
Ils peuvent être d'un type quelconque sauf le type fichier. C'est
une structure hétérogène.
| Tous les identificateurs
de champs d'une même structure enregistrement doivent être différents
à l'intérieur de l'enregistrement. Ils permettent d'accéder
directement aux éléments de l'enregistrement. |
Type
structuré / Enregistrement/partie fixe :
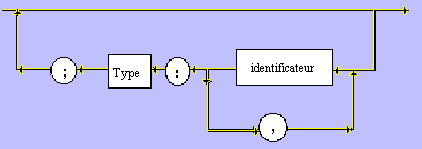
Exemple:
Type
enregis = record
jour : (lundi,mardi,dimanche);
x,y : integer;
mois : 1..12;
T_paie : array[boolean,1..30] of real;
end;
Enregistrement/accès aux champs :

| L'accès aux champs
à l'intérieur d'un enregistrement s'effectue à l'aide
de l'identificateur de l'enregistrement (identif de record), puis
de celui du champs (identif de champs) auquel on désire accéder,
dans cet ordre, comme en désignant un chemin accédant aux éléments
en écrivant de gauche à droite. |
Exemple :
Type
Tenregis =
record
jour : (lundi,mardi,dimanche);
x,y : integer;
mois : 1..12;
T_paie : array[boolean,1..31] of real;
end;
var
A : Tenregis;
begin
A.jour:=;mardi;
A.mois:=8;
A.y:=125;
A.x:=0;
A.T_paie[false,A.mois]
:= -2.37
etc.....
4. Instructions en Pascal
Ce
sont les  traductions des instructions algorithmiques
de notre langage de description formelle d'algorithme que nous avons dénommé
LDFA.
traductions des instructions algorithmiques
de notre langage de description formelle d'algorithme que nous avons dénommé
LDFA.
| LDFA |
Pascal |
| W (instruction vide) |
pas de traduction |
| debut i1 ;
i2; i3; ...... ; ik fin |
begin
i1 ; i2; i3; ...... ; ik end |
| x ¬ a |
x := a |
| ; |
(ordre d'exécution)
; |
| Si P alors
E1 sinon E2 Fsi |
if
P then E1 else E2
( attention défaut,
pas de fermeture !) |
| Tantque P
faire E Ftant |
while P do
E
( attention, pas de
fermeture) |
| répeter
E jusquà P |
repeat E
until P |
| lire (x1,x2,x3......,xn
) |
read(fichier,x1,x2,x3......,xn
)
readln(x1,x2,x3......,xn
)
Get(fichier) |
| ecrire (x1,x2,x3......,xn
) |
write(fichier,x1,x2,x3......,xn
)
writeln(x1,x2,x3......,xn
)
Put(fichier) |
| pour x<-a
jusquà b faire E Fpour |
for x:=a
to b do E (croissant)
for x:=a
downto b do E (décroissant)
( attention, pas de
fermeture)
|
| SortirSi
P |
if P then
Break |
4.1 Instruction d'affectation
L'affectation est applicable à tous les
genres de variables du pascal sauf au type file of.

Sémantique:
- Evaluation de la partie droite (l'expression)
- Transfert de la valeur calculée dans la
partie gauche (la variable)
Exemple :
program Affectation ;
type
Temperature = -20 .. 40 ;
LettreMin = ' a ' .. ' z ' ;
Jour = ( lundi , mardi , mercredi , jeudi ) ;
var
a : integer ; b : char ;
c : string ;
Temp : Temperature ; Lmin : LettreMin
;
Day : Jour ; |
begin
Temp := 18 ;
a := (2+Temp)*4 ;
b := 'F' ;
c := 'bon'+'jour' ;
Lmin
:= 'f' ;
Day
:= mercredi ;
end. |
// Après affectations :
// Temp vaut 18
// a vaut 80
// b vaut 'F'
// c vaut 'bonjour'
// Lmin vaut 'f'
// Day vaut mercredi |
4.2 Instruction de condition

Dans l'instruction
if, l'expression est un prédicat ( expression contenant
des variables, prenant la valeur vrai ou faux), les blocs <instruction>
représentent soit une instruction simple, soit une instruction composée
(begin ..... end).
Sémantique:
cas du if...then
- Si l'expression est vraie, le bloc d'instruction situé
après le then est exécuté et le if...then
s'arrête
- Si l'expression est fausse le if...then
s'arrête.
cas du if...then...else
- Si l'expression est vraie, le bloc d'instruction situé
après le then est exécuté et le if...then...else
s'arrête.
- Si l'expression est fausse, le bloc d'instruction
situé après le else est exécuté et le
if...then...else s'arrête.
Exemple :
program Condition ;
var
x, y ,z : integer ; |
begin
x := 10 ;
y := x*4 ;
if y>100 then z := y
else z := 0;
if z = 0 then
y := 0
x := 0 ;
end. |
// Exécution pas à pas :
// x vaut 10
// y vaut 40
// y>100 est false
donc z vaut 0
// z=100 est true
donc y vaut 0
// x vaut 0
(à la fin : x=0, y=0, z=0) |
4.3 Instruction d'itération while…do
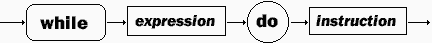
Dans l'instruction while…do, l'expression est un prédicat
( expression contenant des variables, prenant la valeur vrai ou faux), le
blocs <instruction> représente soit une instruction
simple, soit une instruction composée (begin ..... end).
Sémantique:
C'est une instruction
de boucle.
- Tant que l'expression reste vraie, le bloc d'instruction
est réexécuté.
- Dès que l'expression est fausse
le while…do s'arrête.
C'est une boucle non
finie (c-à-dire que l'on ne peut pas connaître dans les cas
de figure si une boucle quelconque de ce type s'arrêtera après
un nombre fini d'exécution).
Exemple :
program WhileDo ;
var
x, y : integer ; |
begin
x
:= 1 ;
y := 0 ;
while x<4 do
begin
x := x+1 ;
y := y +x
end;
writeln ('x=', x , 'y=',
y)
end.
Le programme écrit :
x=4 y=9 |
Exécution pas à pas :
x vaut 1
y vaut 0
x<4 est true
donc x vaut x+1 soit 2
et y vaut
y+x soit
2
x<4 est true
donc x vaut x+1 soit 3
et y vaut
y+x soit
5
x<4 est true
donc x vaut x+1 soit 4
et y vaut
y+x soit
9
x<4 est false donc arrêt
(à la fin : x=4, y=9) |
4.4 Instruction d'itération repeat…until
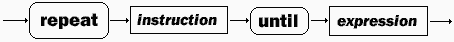
Dans l'instruction
repeat…until, l'expression est un prédicat ( expression
contenant des variables, prenant la valeur vrai ou faux), le blocs <instruction>
représente soit une suite d'instructions simples.
Sémantique:
C'est une instruction
de boucle.
- Tant que l'expression reste fausse, le bloc d'instruction
est réexécuté.
- Dès que l'expression est vraie
le repeat…until s'arrête.
C'est une boucle non finie (c-à-dire que
l'on ne peut pas connaître dans les cas de figure si une boucle quelconque
de ce type s'arrêtera après un nombre fini d'exécution).
La différence avec le while .. do
réside dans le fait que le repeat ... until exécute
toujours au moins une fois le bloc d'instructions avant d'évaluer
l'expression booléenne alors que le while ... do évalue
immédiatement son expression booléenne avant d'exécuter
le bloc d'instructions.
Exemple :
program RepeatUntil ;
var
x, y : integer ; |
begin
x
:= 1 ;
y := 0 ;
repeat
x := x+1 ;
y := y +x
until x>=4;
writeln ('x=', x , 'y=',
y)
end.
Le programme écrit :
x=4 y=9 |
// Exécution pas à pas :
// x vaut 1
// y vaut 0
// on entre dans le repeat
donc x vaut x+1
soit 2
// et y vaut
y+x soit 2
// x>=4 est false
donc x vaut x+1
soit 3
// et y vaut
y+x soit 5
// x>=4 est false
donc x vaut x+1
soit 4
et y vaut
y+x soit 9
// x>=4 est true donc arrêt
(à la fin : x=4, y=9) |
Ce programme fournit le même résultat
que celui de la boucle while…do, car il y a une correspondance sémantique
entre ces deux boucles :
|
repeat <instruction> until <expr>
|
<instruction> ;
while not<expr> do
<instruction>
|
4.5 Instruction
d'itération for…do
C'est une instruction de boucle, il y a deux genres
d'instructions for (for...to et for...downto)
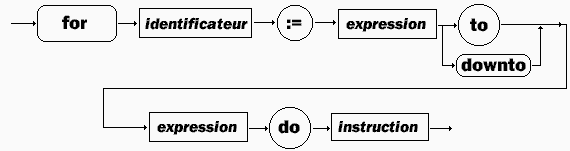
Version
for <identificateur>
:= <Expr1>to
<Expr2> do
<Instruction> :
-
identificateur est une variable qui se dénomme indice
de boucle.
- <Expr1>
et <Expr2> sont obligatoirement
des expressions du même type que la variable d'indice de boucle identificateur.
- < Instruction
> est un bloc d'instruction simple ou composée (begin .....
end).
Version
for <identificateur>
:= <Expr1> downto
<Expr2> do
<Instruction> :
- même signification des constituants que pour
la version précédente, seul le sens de parcours différe
(par valeurs croissantes pour un for...to, par valeurs décroissantes
pour un for...downto).
Sémantique:
L'indice de boucle prend toutes les valeurs (par
ordre croissant ou décroissant selon le genre de for) comprises
entre <Expr1> et <Expr2> bornes inclues.
Tant que la valeur de l'indice de boucle ne dépasse
pas
- par valeur supérieure dans le cas du for...to,
- ou par valeur inférieure dans le cas du
for...downto
la valeur de <Expr2>, le bloc d'instruction est
réexécuté
C'est une boucle finie
(c-à-dire que l'on connaît à l'avance le nombre de tours
de boucle).
Exemple :
program ForDo ;
var x, y : integer ;
begin
y :=0 ;
for
x := 1 to 3 do
y := y +x
end.
|
Exécution de chaque tour de boucle :
y vaut
0
x vaut 1 => y vaut 0+1=1
x vaut 2 => y vaut 1+2=3
x vaut 3 => y vaut 3+3=6
x vaut 4 => arrêt
(à la fin : x=4, y=6) |
4.6 Instruction case…of
C'est une instruction de choix :
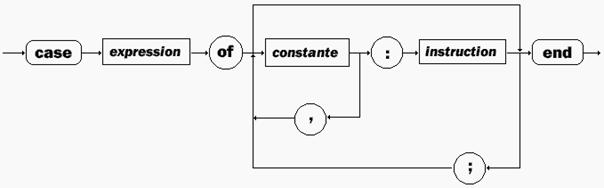
<expression>
doit être de l'un des types : integer, char, boolean, énuméré,
intervalle .
<constante> doit obligatoirement être du même
type que <expression>
<Instruction> est un bloc d'instruction simple ou
composée (begin ..... end).
Sémantique:
C'est une instruction structurée équivalente
à une série de if...then...else imbriqués.
Cette instruction lorsque cela est possible, doit être préférée
à un emboîtement de if...then...else dont
la lisibilité n'est en fait pas optimale.
|
if...then...else
imbriqués
|
case ... of équivalent
|
if x = 3 then E1 else
if x = 4 then E2 else
if x = 5 then E2 else
if x = 6 then E2 else
if x = -5 then E3 else
Ef |
case x of
3
: E1 ;
4..6 : E2 ;
-5 : E3 ;
else Ef
end |
Exemple :
program CaseOf ;
var x, y : integer ;
begin
y :=1 ;
for
x := 0 to 4 do
case x+1 of
0..3 : y :=y*2 ;
4 : y := y+100
else y:=0 ;
end
end.
|
y vaut
1
Exécution du case dans la boucle :
x vaut 0 => x+1 vaut 1 (dans 0..3) => y
vaut 1*2=2
x vaut 1 => x+1 vaut 2 (dans 0..3) => y vaut 2*2=4
x vaut 2 => x+1 vaut 3 (dans 0..3) => y vaut 4*2=8
x vaut 3 => x+1 vaut 4
=> y
vaut 8+100=108
x vaut 4 => x+1 vaut 5 (else) => y vaut 0
x vaut 5 => arrêt
( à la fin : x=4, y=0 ) |
5. Fonctions et procédures en Pascal
Le langage Pascal a
été conçu à l'origine comme un langage
pédagogique d'implantation de la programmation de type algorithmique;
grâce à son extension objet Delphi il est utilisé comme
outil de développement professionnel en entreprise.
La programmation algorithmique est une programmation
hiérarchisée descendante
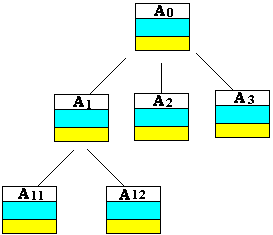
Cette décomposition descendante hiérarchique
est construite à l'aide de blocs de programme notés aussi
des sous-programmes.
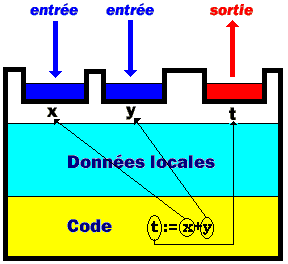
Un bloc comporte donc des données locales,
du code (instructions ou corps du bloc), des données d'entrée
et/ou des données de sortie (permettant les échanges d'informations
entre les différents blocs de la hiérarchie) :
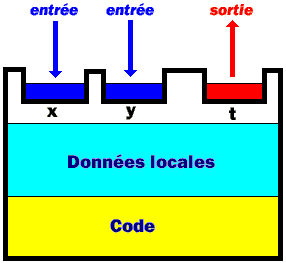
L'exemple ci-après représente trois
blocs B1, B2 et B3 échangeant des informations (en fait chacun calcule
la somme des deux entiers qu'il reçoit en entrée et renvoie
leur somme :
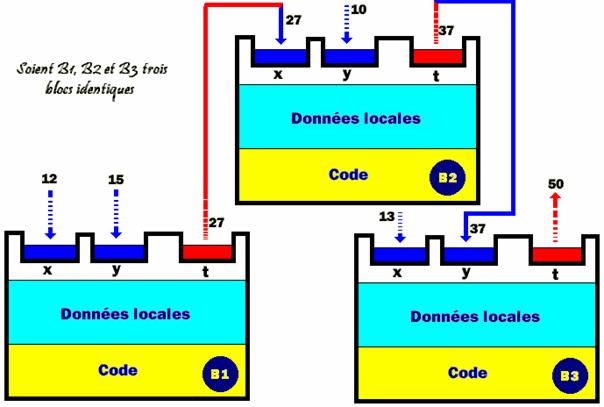
Le bloc B1 reçoit
en entrée 12 et 15 et renvoie la somme 12+15 = 27 vers le bloc B2,
la valeur 27 devient une donnée d'entrée pour le bloc B2 qui
reçoit comme autre entrée la valeur 10. Le bloc B2 renvoie
vers le bloc B3 le résultat 27+10 = 37 etc...
Nous remarquons que
chaque bloc est indépendant des autres blocs. La seule liaison qui
intervienne ici se situe dans le passage des données d'un bloc vers
un autre bloc. Le code et les données locales d'un bloc fixé
sont inaccessibles aux autres blocs.
En pascal les blocs
sont implémentés soit par des fonctions :
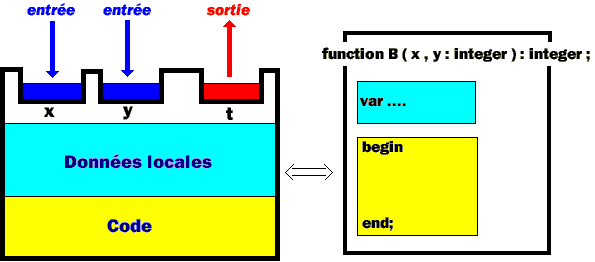
En pascal les blocs sont implémentés
aussi par des procédures :
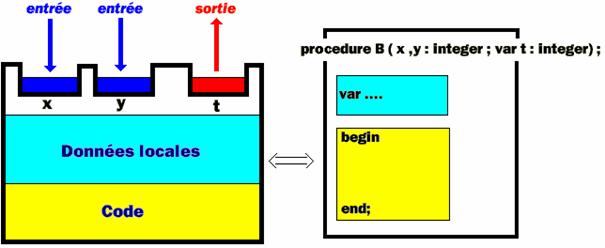
Voici la syntaxe de déclaration des procédures
en Pascal :
Voici la syntaxe de déclaration des fonctions en Pascal :

- <identificateur> est le nom
de la procédure ou de la fonction (choisi par vous)
- <liste de paramètres>
est soit vide, soit elles contient entre parenthèses et séparés
par des point-virgules la liste des paramètres formels.
- <bloc> est une instruction
composée (begin ..... end).
- <identificateur de type>, dans
le cas d'une fonction représente le type du résultat renvoyé
par la fonction.
Exemples de déclarations avec et sans paramètres
formels :
procedure Somme (x,y :integer; var z
:integer) ;
begin
z := x +y
end ;
|
function Somme (x,y :integer): integer ;
begin
result := x +y
end ; |
procedure Somme ;
var x, y : integer ;
begin
y :=1 ; x := 2;
writeln( x+y)
end ; |
function Somme : integer ;
var x, y : integer
;
begin
y :=1 ; x := 2;
result := x +y
end ;
|
6. Paramètres en Pascal
On s’intéresse dans ce paragraphe aux rapports qu’il y a entre
un programme appelant et un sous-programme appelé uniquement en Pascal.
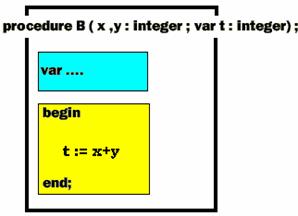
Soit par exemple une procédure B ayant 3
paramètres formels et renvoyant dans le troisième paramètre
la somme des deux premiers :
Les paramètres formels d'une procédure
jouent le rôle de variables muettes et servent à décrire
le fonctionnement d'une procédure. Ils ont la même utilisation
qu'une variable dans un polynôme mathématique. Les deux écritures
P(x) = 3x2 - 4x + 5 et P(t) = 3t2 - 4t + 5 représentent
mathématiquement le même polynôme, il en est de même
pour une procédure.
On peut changer tous les paramètres formels
d'une procédure sans en changer son fonctionnement.
Les deux déclarations ci-dessous sont identiques
:
procedure B (x , y :integer; var t :integer)
;
begin
t := x +y
end ;
procedure B (a , b integer; var c :integer)
;
begin
c := a +b
end ;
|
L'intérêt pratique d'une procédure
et en général d'un sous-programme est essentiellement de pouvoir
exécuter toujours la même action mais avec des valeurs différentes.
Par exemple une procédure P qui utilise
une autre procédure B qui effectue la somme de deux entiers. La procédure
B fonctionne comme une sorte de boîte noire qui reçoit deux
valeurs en entrée et qui retourne leur somme comme dans le pseudo-code
ci-dessous :
Lignes fictives de
code de la procédure P utilisant la boîte noire (procédure
B)
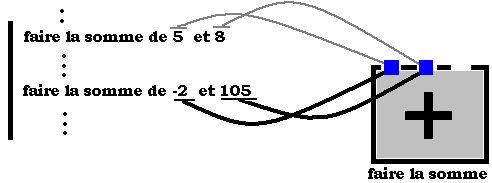
La boîte "faire
la somme" est utilisée une première fois pour sommer 5 et
8, puis plus loin elle est utilisée une deuxième fois pour
sommer -2 et 105.
Le mécanisme qui permet d'utiliser la procédure
B dans le code de la procédure P se dénomme l'appel
de procédure. P se dénomme la procédure appelante.
|
Reprenons l'exemple du polynôme écritures
P(x) = 3x2 - 4x + 5 , nous savons qu'en donnant une valeur effective
à la variable x (par exemple x = 2) on obtient un résultat
noté P(2) qui vaut: P(x) = 3.22 - 4.2
+ 5 = 9.
L'appel de procédure est un procédé
très semblable au calcul du polynôme sur une valeur. La procédure
a besoin qu'on lui fournisse des variables contenant effectivement des valeurs.
De telles variables se dénomment les paramètres effectifs
de la procédure.
|
Précisons un
peu plus l'utilisation d'une procédure S avec des variables. Supposons
que S serve à calculer la somme de deux valeurs 5 et 8
contenues respectivement dans deux variables locales a et b
d'une autre procédure nommée P dont le seul paramètre
x renvoie le résultat 13 du calcul obtenu par appel
de la procédure B dans le code de la procédure P :
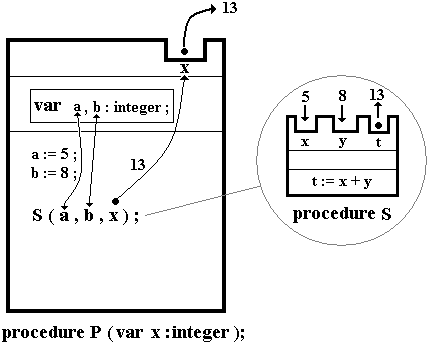
L'appel S(a,b,x) s'effectue
sur des paramètres effectifs qui sont nécessairement des variables
existantes, soit déclarées dans un paragraphe var dans la
zone des données locales, soit déclarées en tant que
paramètres de la procédure appelante.
L'appel se fait avec un nombre de paramètres
effectifs ègal à celui des paramètres formels en respectant
l'ordre et la cohérence des types. On peut imaginer que lors d'un
appel à la procédure S par le code de la procédure S,
le code de la procédure S vient s'imbriquer fictivement dans
le code de P à l'endroit de l'appel avec comme variables les paramètres
effectifs :
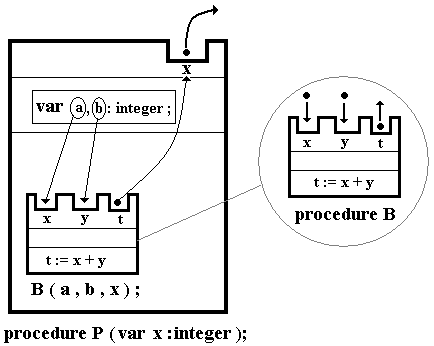
Comment a lieu
cet appel, cette inclusion fictive du code ?
|
On dénomme l'action qui consiste à
appeler sur des paramètres effectifs, le passage des paramètres
effectifs ou encore la transmission des paramètres
effectifs.
Il faut savoir qu’un paramètre effectif
transmis au sous-programme appelé est un moyen d’utiliser ou
d’accéder à une information appartenant au bloc appelant
(le bloc appelé peut être le même que le bloc appelant,
il s’agit alors de récursivité).
|
Pascal ne dispose que de 2 modes de passage sur les 5 modes généraux
:
- le passage par référence
ou adresse.
|
6.1 Lecture seulement : passage par valeur
Dans un passage par valeur, le paramètre
formel est considéré comme une variable locale dans le corps
du sous-programme. Sa valeur est initialisée au début de chaque
exécution du sous-programme avec la valeur du paramètre effectif
correspondant.
Il y a recopie de la valeur du paramètre
effectif dans une zone spécifique locale à la procédure.
Toutes les opérations qui sont effectuées sur le paramètre
formel n’affectent que cette valeur locale.
|
Ecriture en Pascal procedure sp(... x: real ....)
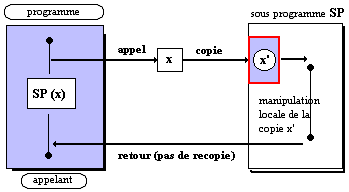
passage par valeur
6.2 Accès direct : passage par adresse
ou par référence
Dans un passage par
adresse le paramètre formel est traité comme une variable
dont l’adresse qui est transmise au moment de chaque appel, est celle du
paramètre effectif correspondant. L’adresse de la variable
effective autorise toutes les modifications immédiatement sur cette
variable quelle que soit sa localisation.
Ecriture en Pascal
procedure sp (....var x : real .....)
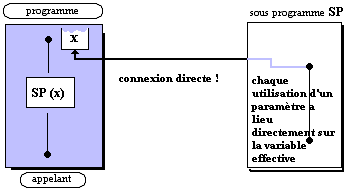
passage par référence
Comparaison des avantages et des
inconvénients des 2 modes
Passage par valeur :
- Avantage : sécurité et protection des informations.
- Inconvénient : lenteur due à la recopie des données
et doublement de la place mémoire occupée (mais convient
bien pour des variables simples !).
|
Passage par référence
:
- Avantage : rapidité d’accès aux données,
moindre occupation mémoire puisqu’il ne s’agit que d’une adresse.
- Inconvénient : ce mode est dangereux à cause de la non
protection des données et de la nécessité qu’il y
a de connaître la façon dont sont implantées physiquement
les données sur la machine.
|
Ces
deux modes de passage des paramètres sont présents dans des
langages comme C++, java, Ada, Visual-Basic .net, Delphi et C#. Ils
suffit donc pour le débutant, de bien comprendre le processus avec
le pascal et par analogie il pourra l'utiliser avec les autres langages.
Exemple :
procedure B1 (x : integer; var y : integer)
;
begin
y := 10*x
end ;
|
Dans la procédure B1
x est passé par valeur
y est passé par référence
|
procedure B2 (x : integer; y :integer) ;
begin
y := 10*x
end ;
|
Dans la procédure B2
x est passé par valeur
y est passé par valeur
|
procedure P ;
var a , b: integer ;
begin
a := 100 ;
b := 0 ;
B1 ( a , b
) ;
a := 100 ;
b := 0 ;
B2 ( a , b
) ;
end ;
|
Dans la procédure P
Appel de B1
B1( valeur a , ref b)
Résultat après appel :
b = 1000
Appel de B2
B2( valeur a , valeur b)
Résultat après appel :
b = 0 |
7. Fonction ou procédure
?
Une fonction est un bloc de programme qui réalise des traitements
et renvoie une valeur unique, c'est une procédure ne possédant
qu'un seul élément de sortie (appelé paramètre).
Tout
ce qui a été énoncé sur les procédures
s'applique in extenso aux fonctions.
La ligne : "procedure B ( x , y : integer
; var t : integer) ; "
se dénomme l'en-tête
de la procédure.
La ligne : "function B ( x
, y : integer ) : integer ; "
se dénomme l'en-tête
de la fonction
|
En pascal les blocs peuvent être implémentés aussi
par des fonctions mais uniquement lorsqu'il n'y a qu'une donnée
de sortie (un seul résultat).
Exemple1 :
function B1 (x : integer ) : integer ;
begin
result := 10*x
end ;
procedure P ;
var
a , b: integer
;
begin
a := 100 ;
b := B1 ( a )
end ; |
Dans la function B1
x est passé par valeur
B1 renvoie un résultat de
type integer
Dans la procédure P
Appel de la fonction B1
b := B1( valeur
a )
Résultat après appel :
b = 1000
|
Exemple2 :
function TTC (PHT,Tva : real ) : real ;
begin
result := PHT*Tva
end ;
procedure CalculPrix ;
var
PrixHT ,
PrixTTC : real ;
begin
PrixHT:= 100
;
PrixTTC := TTC
( PrixHT , 1.186 )
end ;
|
Dans la function TTC
PHT et Tva sont passés par
valeur
TTC renvoie un résultat de type
real qui est
Le paramètre prix hors taxe multiplié
par le paramètre taux de TVA.
Dans la procédure CalculPrix
PrixHT = 100 €
Appel de la fonction TTC
PrixTTC := TTC ( valeur a , 1.186
)
Résultat après appel :
PrixTTC = 118,6 €
|
Les déclarations de fonctions et de procédures
suivent le schéma grammatical de la déclaration générale
du programme principal :
< Déclaration de procédure
>
procedure <identif de proc>
<liste de paramètres formels>
;
 ;
;
Exemple
:
procedure
Calcul (x
: integer; var y :integer) ;
<identif de proc> <liste de paramètres formels>
var
a, b : integer ; <déclarations>
begin
x := a*x ; <instruction>
y := x - b ; <instruction>
end ;
< Déclaration de fonction >
function <identif de fonc> <liste
de paramètres formels> : <type
du résultat> ;

Exemple :
function
Calcul (x
: integer)
:
integer ;
<identif de fonc> <liste de paramètres formels>
<type du résultat>
var a : integer ; <déclarations>
begin
result := a*x ; <instruction>
end
;
8. Visibilités des variables
Le langage pascal suivant méthode de la programmation structurée
descendante, les déclarations de fonctions/procédures peuvent
être imbriquées :
< Déclarations > :
Exemple de déclarations imbriquées
dans la même procédure P0 :
procedure P0 (x,y,z : char) ;
var
a , b: integer ;
procedure P1 ( var u : integer) ;
var
a , b: integer
;
procedure P11 ( var u,v,w : integer)
;
var
a , b: integer
;
begin
…..
end ;
procedure P12 ( t : integer; h :char) ;
var
a , b: integer
;
begin
…..
end ;
begin { P1
}
…..
end ; { P1
}
|
procedure P2 ( f, g, h : real) ;
var
a , b: integer
;
procedure P21 ( n, m, p : integer) ;
var
a , b: integer
;
begin
…..
end ;
begin { P2 }
…..
end ; { P2
}
begin { P0 }
…..
end ; { P0 }
|
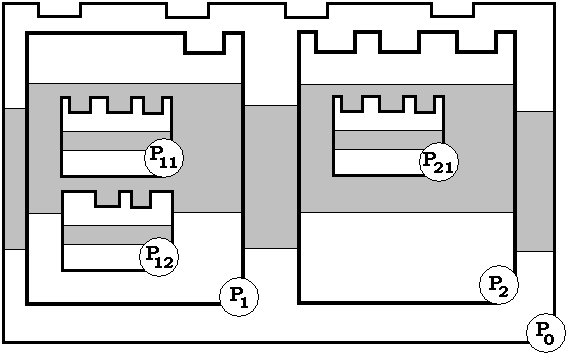
Ecritures que l'on peut représenter schématiquement
par les imbrications de blocs qui suivent (les parties grisées d'un
bloc correspondent à la partie déclaration du bloc) :
Supposons dans l'exemple précédent
que la partie déclaration de chaque bloc contienne outre l'éventuelle
déclaration d'un autre bloc, des déclarations de variables
(a dans le bloc P0, b dans le bloc P1, c dans le bloc
P11, d dans le bloc P12, e dans le bloc P2, f dans
le bloc P21 ) :
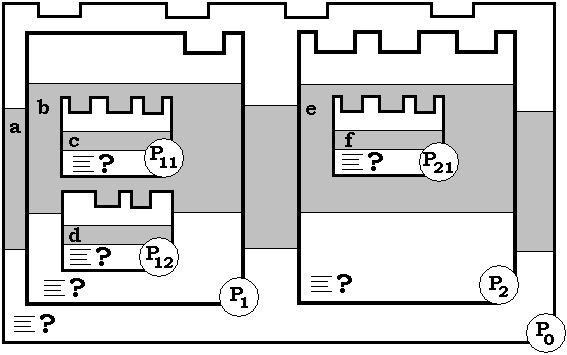
Code pascal du schéma
précédent :
procedure P0 (x,y,z : char) ;
var
a : integer ;
procedure P1 ( var s : integer) ;
var
b : integer
;
procedure P11 ( var u,v,w : integer)
;
var
c : integer
;
begin
….. ?….
end ;
procedure P12 ( t : integer; h :char) ;
var
d : integer
;
begin
….. ?….
end ;
begin { P1 }
….. ?….
end ; { P1 }
|
procedure P2 ( f, g, h : real) ;
var
e : integer
;
procedure P21 ( n, m, p : integer) ;
var
f : integer
;
begin
….. ?….
end ;
begin { P2 }
….. ?….
end ; { P2
}
begin { P0 }
….. ?….
end ; { P0 }
|
Etant donné les possibilités offertes
par cette disposition des blocs en Pascal, il vient immédiatement
une question sur les accès autorisés ou non aux données
situées dans les parties déclarations des blocs P0, P1, etc...
En d'autres termes, dans la partie code de chaque
bloc quelles variables peut-on utiliser ? Par exemple dans le corps (la
partie code) de la procédure P12 peut-on utiliser toutes les variables
a, b, c, d, e, f ou bien seulement certaines et selon quelles règles
?
procedure P12 ( t : integer; h :char) ;
var d : integer ;
begin
….. ?….
end ;
Ces autorisations d'accès aux données
situées dans des blocs imbriquées sont contenues dans la notion
de règle de visibilité dans les langages à structure
de bloc (Pascal en est un cas particulier, ces règles s'appliqueront
aussi à d'autres langages)
Règle de visibilté :
|
Toute donnée X déclarée localement
dans un bloc Pk n'est visible que :
- dans le bloc où elle
est déclarée,
- et dans tous les blocs Pk+n imbriqués
dans Pk.
- Un paramètre formel
est considéré comme une variable locale au bloc.
|
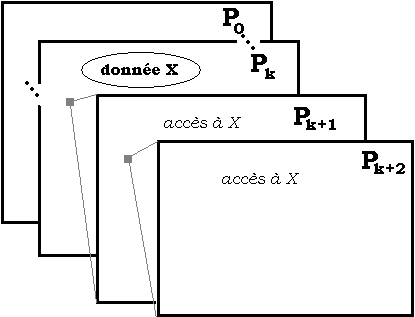
fig
- visibilité d'une donnée X déclarée dans Pk
Remarque : masquage
Lorsqu'une donnée déclarée
sous le nom X dans un bloc Pk est redéclarée sous
le même nom X dans un bloc Pk+n imbriqué dans Pk
, on dit alors que la donnée X de Pk+n masque
les informations contenues dans la donnée X de Pk dans
le bloc Pk+n et dans ceux qu'ils contient.
|
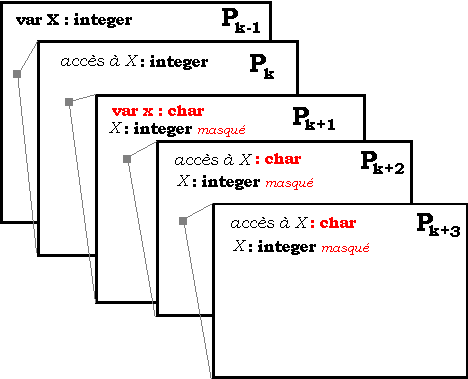
fig - visibilité d'une donnée X déclarée dans
Pk-1
Etudions la visibilité des variables a,
b, c, d, e, f dans les blocs P0, P1, P11, P12, P2, P21 figurés
ci-dessous :
procedure P0 (……) ;
var
a : integer ;
procedure P1 ( …….) ;
var
b : integer
;
procedure P11 ( …………) ;
var
c : integer
;
begin
….. ?….
end ;
procedure P12 ( …………) ;
var
d : integer
;
begin
….. ?….
end ;
begin { P1 }
….. ?….
end ; { P1
}
|
procedure P2 ( ………. ) ;
var
e : integer
;
procedure P21 ( ……….. ) ;
var
f : integer
;
begin
….. ?….
end ;
begin { P2 }
….. ?….
end ; { P2
}
begin { P0 }
….. ?….
end ; { P0 }
|
Etablissons à partir de la règle
de visibilité énoncée plus haut, deux tableaux récapitulatifs
croisés de la visibilité des variables a, b, c, d, e, f
:
|
variable
|
Bloc où cette variable est visible
|
|
Bloc
|
variables visibles dans ce bloc
|
|
a
|
P0, P1, P11,
P12, P2, P21
|
|
P0
|
a
|
|
b
|
P1, P11, P12
|
|
P1
|
a,
b
|
|
c
|
P11
|
|
P11
|
a,
b, c
|
|
d
|
P12
|
|
P12
|
a,
b, d
|
|
e
|
P2, P21
|
|
P2
|
a,
e
|
|
f
|
P21
|
|
P21
|
a,
b, f
|
Nous pouvons donc répondre maintenant aisément
à la question posée plus haut : quelles variables peut utiliser
dans la procédure P12 ?
La procédure P12 accède aux variables
a, b et d, ( avec en plus comme variables locales ses paramètres
formels t et h ) :
procedure P12 ( t : integer; h :char) ;
var d : integer ;
begin
// accès aux variables
a, b, d, t et h,
end ;
9. Variables dynamiques ou pointeurs
Définition
Beaucoup de langages disposent de la notion de pointeur C++ en particulier.
C’est une notion proche de la machine qui a été utilisée
dès le début pour représenter dans un programme l’allocation
dynamique de mémoire. Dans une structure à allocation
dynamique de mémoire le compilateur ne connaît pas à l’avance
la taille de la structure, la gestion de la mémoire est alors confiée
au programmeur. C’est lors de l’exécution et au fur et à mesure
des mises à jours que la taille de la structure varie, comme par exemple
dans la gestion d’une liste dont la taille varie en fonction des ajouts ou
des suppressions. A l’opposé, une structure statique est une entité
dont le compilateur connaît très exactement la taille avant
l’exécution du programme, comme par exemple la structure de données
de type tableau peut être considérée comme une structure
statique puisque la taille du tableau (nombre de cellules) est connue lors
de la déclaration.
En fait, les langages récents ne disposent plus de cette notion de
pointeurs ou variables dynamiques parce qu’à l’usage elle s’est révélée
dangereuse car trop proche de la machine laissant le programmeur se débrouiller
seul avec la gestion de la mémoire, elle est utilement remplacée
par la notion de référence d’objet comme dans Java, le langage
C# demandant une autorisation pour traiter du code non sûr (unsafe code).
Delphi quant à lui, combine les deux outils : pointeurs et références
d’objet,la version Delphi 8.Net adoptant la même démarche que
C# (unsafe code).
La notion de pointeur très présente, voir même essentielle
dans un langage comme le C, est utilisable en pascal.
Prenons par exemple une variable numérique N entière
d’adresse en mémoire centrale 19432 et contenant le nombre entier 235,
nous appelons x un pointeur vers cette variable N, une variable dynamique
contenant l’adresse de la variable N :
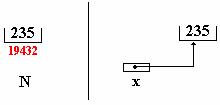
Nous dirons aussi que x « pointe » vers la variable N et que
le « contenu » de x est 235.
En pascal (utiliser Delphi en mode console), une variable dynamique se
déclare comme une variable classique mais le type est précédé
du symbole « ^ », elle est typée (le type de la donnée
vers laquelle elle pointe), mais sa gestion est entièrement à
la charge du programmeur à travers les procédures d’allocation
et de désallocation mémoire respectivement appelées new
et dispose
Utilisation pratique des variables dynamiques
Contenu d’une variable dynamique « x »
déjà allouée : il est noté «
x^ »
Dans l’exemple précédent :
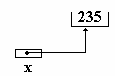
|
x^ vaut 235 (contenu de la variable
dynamique)
x vaut 19432 (adresse de la variable dynamique)
|
Détaillons pas à pas un programme
d’utilisation de pointeur
|
Soit l’exemple
précédent :
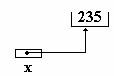
Le programme de droite écrit sur l’écran
le « contenu » de la variable x (contenu de la cellule
pointée par x) soit : x vaut : 235.
|
Voici le programme
à analyser :
program VarDyn;
var
x : ^integer;
begin
new(x);
x^:= 235;
writeln(‘x vaut: ‘,x^);
dispose(x);
end.
|
Déclaration
d’une variable dynamique « x » de type entier :
|
Soit l’instruction :
var x : ^integer ;
|
Résultat
produit :
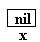
x est créée (mais x ne pointe vers
rien encore)
x
vaut nil
|
Allocation d’une
variable dynamique « x » déjà déclarée :
|
Soit l’instruction :
new ( x ) ;
|
Résultat
produit :
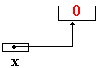
une
cellule mémoire de type integer est crée,
x pointe vers la cellule créée.
(x
vaut la valeur de l’adresse de la cellule)
|
Affectation du contenu
d’une variable dynamique « x » déjà déclarée :
|
Soit l’instruction :
x^ := 235 ;
|
Résultat
produit :
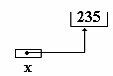
La cellule
mémoire pointée par x contient 235.
|
Désallocation
d’une variable dynamique « x » déjà allouée :
|
Soit l’instruction :
dispose ( x ) ;
|
Résultat
produit :
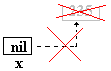
La cellule mémoire qui contenait 235 n’existe
plus, elle est rendue au système (ont dit désallouée)
|
Attention
Ne pas confondre l’effacement
de l’adresse d’une variable dynamique et sa désallocation.
Effacement de l’adresse
d’une variable dynamique : mot clef « nil »
Désallocation
d’une variable dynamique : procédure dispose(…)
|
Soit l’exemple
précédent :

|
Résultat
produit par x := nil :
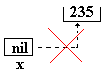
- x^
n’existe plus (x ne
pointe vers plus rien)
- x
vaut nil
- La cellule
mémoire qui contient 235 existe toujours, mais n’est
plus accessible !
|
|
Résultat
produit par dispose ( x ) :

- x^
n’existe plus (x ne
pointe vers plus rien)
- x
vaut nil
- La cellule
mémoire qui contenait 235 n’existe plus !
|
C’est en particulier cette dernière remarque
qui pose le plus de soucis de maintenance aux développeurs utilisant
les pointeurs (par ex : problème de la référence
folle).
Affectation de variables
dynamiques entre elles :
On suppose que deux
variables dynamiques « x et y » de type ^integer
ont été déclarées et créées par
la procédure new, nous figurons ci-après l’incidence
de l’affectation x := y sur ces variables :
|
Soient les instructions :
x^ := 235 ;
y^ := 1098 ;
Soit l’affectation :
x := y ;
x et y pointent vers la même cellule mémoire
|
Résultat produit :

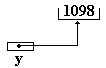
Résultat produit :
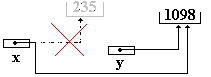
|
Une structure de données récursive
avec pointeurs
Prenons une structure
de données organisée sous forme de liste composée de
cellules qui sont elles mêmes chacune un enregistrement (un record)
contenant deux champs num et suite :
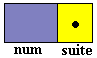
Le champ num est de type entier, et le champ
suite est une variable dynamique de type cellule (lorsqu’il est
alloué, il pointe donc vers une nouvelle cellule) :
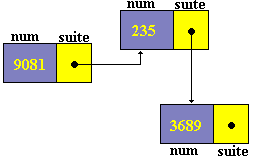
Soit un programme d’exemple
de structure récursive (Delphi en mode console) utilisant les
variables dynamiques pour représenter cette structure.
|
program pointeur;
type
cell = ^struct;
struct = record
num
: integer;
suite
: cell
end;
var
x , y, z , t , u : cell;
|
begin
new(x) ;
x^.num := 10;
new(y) ;
y^.num := 20;
new(z) ;
z^.num := 30;
new(t) ; t^.num
:= 40;
new(u) ; u^.num
:= 50;
end.
Ce
programme crée 5 cellules :
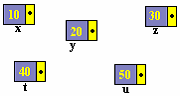
|
|
Les
instructions suivantes :
t^.suite := x;
x^.suite := y;
z^.suite := u;
u^.suite := y;
|
représentent les liens ci-dessous :
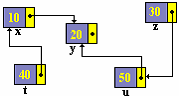
|
|
L’instruction suivante
|
Représente
l’accès au lien
|
Et
écrit sur la console
|
|
writeln ( t ^. suite^. num);
|
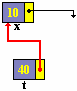
|
10
(le contenu du champ num de x)
|
|
writeln ( u^. suite^. num);
|
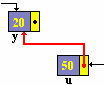
|
20
(le contenu du champ num de y)
|
|
writeln ( t ^.suite^.suite^.num);
|
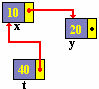
|
20
(le contenu du champ num de y)
|
|
writeln ( z ^.suite^.suite^.num);
|
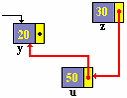
|
20
(le contenu du champ num de y)
|
La notion de référence est abordée au chapitre sur la
programmation objet, c’est en fait un pointeur entièrement encapsulé
sur lequel il n’est possible de faire qu’une seule opération :
l’affectation de référence.
De nombreux exemples simples
sont disponibles dans  le tuteur Pascal associé
à ce logiciel.
le tuteur Pascal associé
à ce logiciel.
10. Récursivité en programmation
Définition
Une famille d'objet est dite récursive, si dans sa définition
il est fait référence à la famille elle-même.
Pour un langage de programmation, nous dirons
qu'il autorise la récursivité si un sous-programme peut s'appeler
lui-même directement ou indirectement à travers un autre sous-programme.
Le langage de programmation Algol 60 a été le précurseur
sur le sujet de la récursivité. D'une manière générale
un langage de programmation récursif doit donc être capable
dans son implémentation, de conserver les contextes successifs provenant
de chaque appel récursif du sous-programme.
Pour les langages à structure de bloc le problème de la conservation
des contextes successifs est résolu grâce à la pile d'exécution
dynamique : les variables locales et les paramètres sont empilés
à chaque appel récursif du sous-programme.
Récursivité directe et indirecte en Pascal-Delphi :
|
Récursivité directe |
Récursivité indirecte ou croisée |
|
Procedure P ;
Begin
….. P ;
End; |
Procedure A ;
Begin
….. C ;
End;
|
Procedure B ;
Begin
….. A ;
End;
|
|
Procedure C ; Begin
….. B ;
End;
|
Notons que dans le cas de la récursivité croisée, il existe un problème
syntaxique de déclaration d'une procédure avant l'autre :
|
Procedure A ;
Begin
….. B ;
End;
|
Procedure B ;
Begin
….. A ;
End;
|
La directive forward sert à résoudre ce problème. Lors de la déclaration, cette directive sert à déclarer syntaxiquement l'en-tête d'une procédure qui sera déclarée en totalité plus loin. Cette directive permet d'utiliser la récursivité croisée en particulier :
|
Procedure B ; forward ;
Procedure A ;
Begin
….. B ;
End;
|
Procedure B ;
Begin
….. A ;
End;
|
Exemples en Pascal-Delphi de base
Le traitement de problème relatifs à des suites récurrentes
ou de définition récurrentes (du genre Un = f(Un-1)) peut s'effectuer à l'aide de la récursivité.
1°) Définition récursive de la fonction puissance entière xn :
xn = xn-1 * x , "n Î N*
x0 = 1
Implantation en Pascal-Delphi :
function puissance ( n : integer; x : real) : real ;
begin
if n = 0 then result := 1
else result := x*puissance (n-1,x)
end;
2°) Définition récursive de la fonction factorielle du nombre entier n :
n ! = (n-1)!* n , "n Î N*
0 ! = 1
Implantation en Pascal-Delphi :
function fact ( n : integer ) : integer;
begin
if n = 0 then result := 1
else result := x* fact (n-1)
end;
3°) Définition récursive du pgcd de 2 entiers a et b par la méthode d'Euclide :
"a, a Î N*, "b, b Î N*
pgcd ( a et b ) = pgcd ( b et reste (a par b) )
Implantation en Pascal-Delphi :
( l'opérateur mod du pascal permet de calculer le reste de la division de a par b , on note : "a mod b" )
function pgcd1 ( a,b : integer ) : integer;
begin
if b = 0 then result := a
else result := pgcd1 (b, a mod b)
end;
4°) Définition récursive du pgcd de 2 entiers a et b par la méthode Egyptienne :
"a, a Î N*, "b, b Î N*
pgcd ( a et b ) = pgcd ( b , a-b ), si a ³ b
pgcd ( a et b ) = pgcd ( a , b-a ), si b > a
Implantation en Pascal-Delphi :
function pgcd2 ( a , b : integer ) : integer;
begin
if a = b then result := a
else
begin
if a < b then result := pgcd2( a , b-a )
else result := pgcd2( b , a-b )
end
end;
5°) Programmation récursive de l'inversion d'une chaîne de caractères :
Soit à construire une fonction qui reçoit une chaîne
de type string et qui renvoie cette chaîne inversée.
Implantation en Pascal-Delphi :
function InvCh ( ch : string ) : string;
begin
if length(ch) < 2 then result := ch // si ch est vide ou si ch n'a qu'un seul caractère
else result := InvCh ( Copy(ch , 2 , length(ch)-1 ) + ch[1]
end;
6°) Procédure récursive de recherche dichotomique dans un tableau trié :
Soit à construire une procédure permettant de rechercher un élément x dans un tableau table et de renvoyer son rang ou -1 si l'élément n'est pas présent.
Implantation en Pascal-Delphi :
type
Elmt = integer ;
tableau = array[1..max] of Elmt ;
procedure dichoRecur(x : Elmt; table:tableau; g,d:integer; var rang:integer) ;
{ recherche dichotomique récursive dans table
rang =-1 si pas trouvé. g, d : 0..max+1}
var
milieu:1..max;
begin
if g <= d then
begin
milieu := (g+d) div 2;
if x=table[milieu] then rang:=milieu
else
if x < table[milieu] then dichoRecur(x, table, g, milieu-1, rang)
else dichoRecur(x, table, milieu+1, d, rang)
end
else rang:=-1
end; {dichoRecur}
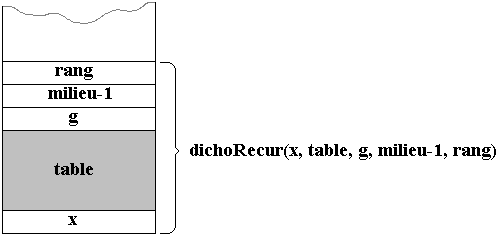
Pile d'exécution du contexte du premier appel récursif de dichoRecur(x, table, g, milieu-1, rang)
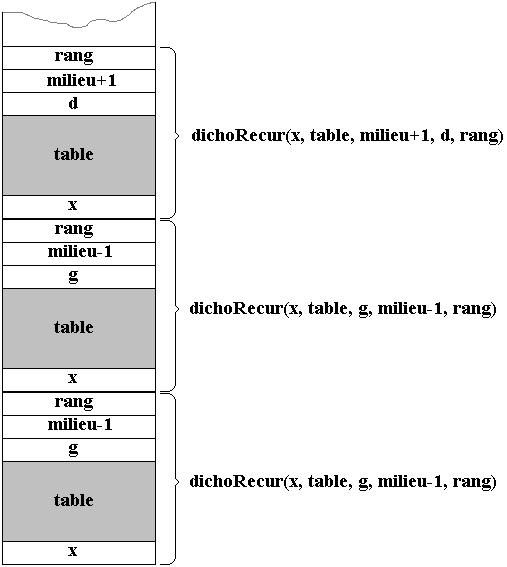
Empilement des contextes de trois appels récursifs de la procédure dichoRecur :
dichoRecur(x, table, g, milieu-1, rang)
dichoRecur(x, table, g, milieu-1, rang)
dichoRecur(x, table, d, milieu+1, rang)