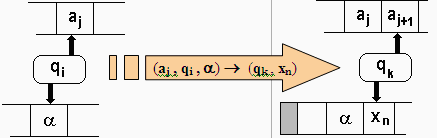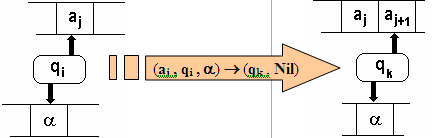3.1.Programmation avec
les grammaires de type 2 (exemples
de classes en Delphi et Java)
Plan
du chapitre: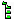
1. Programmation par les grammaires
1.1 Méthode pratique de programmation en pascal
1.2 Application de la méthode : un mini-français
2. C-grammaire et automate à pile de mémoire
2.1 Définition d’un
automate à pile
2.2 Algorithme de fonctionnement
d’un automate à pile
2.3 Programme Pascal simple
d’un automate à pile
2.4 Programme Delphi d’une classe
d'automate à pile
D’un point de vue pratique, les
grammaires sont un outil abstrait puissant. Nous avons vu qu’elles permettaient
de décrire des langages de quatre catégories. Elles servent
aussi :
- soit à générer
des phrases dans le langage engendré par la grammaire (en ce sens
elles permettent la programmation),
- soit à analyser
un énoncé quelconque pour savoir s’il appartient ou non au
langage engendré par la grammaire (en ce sens elles permettent la
construction des analyseurs et des compilateurs).
1. Programmation
par les grammaires
Nous adoptons ici le point de
vue " mode génération " d’une grammaire afin de s’en servir
comme d’un outil de spécification sur les mots du langage engendré
par cette grammaire. On appelle aussi cette démarche programmation
par la syntaxe.
Nous nous restreindrons au C-grammaires
et aux grammaires d’états finis. Soit G = (VN,VT,S,R),
une telle grammaire et L(G) le langage engendré par G.
Objectif :
Nous
voulons construire un programme qui nous exhibe sur l’écran des
mots du langage L(G).
1.1 Méthode pratique
de programmation en pascal
G = (VN,VT,S,R)
à
traduction en programme pascal générateur de mots.
La grammaire G est supposée ne pas contenir de règle
récursive gauche, sinon il faut essayer de la changer ou abandonner.
1° Tous les éléments du vocabulaire auxiliaire
VN deviennent les noms d’une procédure pascal.
2° Le vocabulaire terminal VT est décrit
soit par un type prédéfini pascal s’il est simple, sinon
par une structure de donnée et un TAD.
3° Toutes les règles de G sont traduites de cette
manière :
3.1° le symbole de VN de la partie Gauche de
la règle indique le nom de la procédure que l’on va implanter.
3.2° la partie droite d’une règle correspond à
l’implémentation du corps de la procédure, pour chaque symbole
a de cette
partie droite si c’est :
- un élément de VT, il est traduit
par une écriture de sa valeur (généralement un writeln(a)).
- un élément de VN, il est traduit par
un appel à la procédure pascal du même nom que lui.
4° La procédure représentant l’axiome S est
appelée dans le programme principal. Chaque appel de S fournira un
mot du langage L(G).
Afin de bien persuader
le lecteur de la non dépendance de la méthode vis à
vis du langage nous construisons l'exemple en parallèle en Delphi
et en Java.
Exemple fictif :
Grammaire
|
Traduction
en Delphi
|
Traduction
en Java
|
G = (VN,VT,S,R)
VN = {S,A,B}
VT = {a,b}
Axiome :
S
Règles
:
......
k :S ¾® aAbBb |
VN ¾®
procedure
S ;
VT ¾® Type Vt = char ;
procedure A ;
procedure B ;
|
VN ¾® void S( ) ;
VT ¾® char ;
void A( ) ;
void B( ) ;
|
La règle k est traduite
par l’implantation du corps de la procédure associée à
l’axiome S (partie gauche):
Règle
|
Traduction
en Delphi
|
Traduction
en Java
|
| k :S ¾® aAbBb |
procedure S ;
begin
writeln(‘a’) ;
A ;
writeln(‘b’) ;
B ;
writeln(‘b’) ;
end;
|
void
S ( ) {
System.out.println('a');
A( ) ;
System.out.println('b');
B( ) ;
} |
Le lecteur comprend ici le pourquoi
de la contrainte de règles non récursives gauches (du genre
A ¾® A a), la procédure s’écrirait alors :
Règle
|
Traduction
en Delphi
|
Traduction
en Java
|
| A ¾® A a |
procedure A ;
begin
A ;
...
end ;
|
void A ( ) {
A( ) ;
...
} |
Ce qui conduirait le programme
à un empilement récursif infini(limité par la saturation
de la pile d’exécution de la machine).
1.2 Application de la méthode
: un mini-français
 Pascal.ProgGramTyp2\Minifr1.pas
Pascal.ProgGramTyp2\Minifr1.pas
Etant donné G une grammaire
d’un sous-ensemble du français .
G = (VN,VT,S,R)
VT ={le, un, chat, chien, aime, poursuit,
malicieusement, joyeusement, gentil, noir, blanc, beau}
VN = {áphraseñ,
áGNñ, áGVñ, áArtñ, áNomñ, áAdjñ, áAdvñ, áverbeñ}
Axiome : áphraseñ
Règles :
1 :á phrase
ñ¾®á GN ñá GV ñá GN ñ.
2 :á GN
ñ¾®á
Art ñá Adj ñá Nom ñ
3 :á GN
ñ¾®á Art ñá Nom ñá Adj ñ
4 :á GV
ñ¾®á verbe ñ |
á verbe ñá Adv ñ
5 :á Art
ñ¾® le | un
6 :á Nom
ñ¾® chien | chat
7 :á verbe
ñ¾® aime | poursuit
8 :á Adj
ñ¾® blanc | noir | gentil | beau
9 :á Adv
ñ¾® malicieusement | joyeusement
Traduisons à l’aide de
la méthode précédente, cette grammaire G en un programme
pascal générant des phrases de L(G).
A) les
procédures du programme
Chaque élément
de VN est associé à une procédure
:
| VN = {áphraseñ,
áGNñ, áGVñ, áArtñ, áNomñ, áAdjñ, áAdvñ, áverbeñ} |
VN
|
Traduction
en Delphi
|
Traduction
en Java
|
| { áphraseñ,
áGNñ, áGVñ, áArtñ, áNomñ, áAdjñ, áAdvñ, áverbeñ } |
procedure phrase;
procedure GN;
procedure GV;
procedure Art;
procedure Nom;
procedure Adj;
procedure Adv;
procedure verbe;
|
void phrase( )
void GN( )
void GV( )
void Art( )
void Nom( )
void Adj( )
void Adv( )
void verbe( )
|
B)
les types de données associés à VT
Nous utilisons la structure de
tableau de chaînes, commode à cause de sa capacité
d’accès direct pour stocker les éléments de VT.
Toutefois, au lieu de ne prendre qu’un seul tableau de chaînes pour
VT tout entier, nous partitionnons VT
en 5 sous-ensembles disjoints :
VT = tnom È tadjectif È tarticle È tverbe È tadverbe
où
:
tnom={ chat, chien } tadjectif={
blanc, noir, gentil, beau }
tarticle ={ le, un } tverbe
={ aime, poursuit }
tadverbe={ malicieusement,
joyeusement } |
Spécification d’implantation
:
Ces cinq ensembles sont donc
représentés en Pascal chacun par un tableau de chaînes.
Nous définissons le type mot comme le type général,
puis cinq tableaux de type mot.
const
Maxnbmot=4;
// nombre maximal de mots dans un tableau
type
mot
= array[1..Maxnbmot]of string;
var
tnom,tadjectif,tarticle,tverbe,tadverbe:mot; |
Nous construisons une classe
que nous nommons Gener_fr qui est chargée de construire et d'afficher
une phrase du langage mini-fr :
Tous les champs seront privés la seule méthode publique
est la méthode phrase qui traduit l'axiome de la grammaire et qui
lance le processus de génération et bienentendu le constructeur
d'objet de la classe qui est obligatoirement publique.
Etat de la classe à ce niveau de construction :
const
Maxnbmot = 4 ; // nombre maximal de mots dans un tableau
type
mot = array
[1..Maxnbmot] of
string
;
Gener_fr = class
private
tnom, tadjectif, tarticle, tverbe, tadverbe
: mot ;
procedure GN ;
procedure GV ;
procedure Art ;
procedure Nom ;
procedure Adj ;
procedure Adv ;
procedure verbe ;
public
constructor Creer ;
// constructeur d'objet
procedure
phrase
;
// axiome de la grammaire
end;
Spécification d’implantation en Java : Les spécifications
sont les mêmes qu'en Delphi
Etat de la classe Java à ce niveau de construction :
class
Gener_fr
{
final int Maxnbmot
= 4 ; // nombre maximal de mots dans un tableau
private
String
[ ] tnom ;
private String [ ] tadjectif
;
private String [ ] tarticle
;
private String [ ] tverbe
;
private String [ ] tadverbe
;
private void GN ( ) {
}
private void GV ( ) {
}
private void Art ( ) {
}
private void Nom ( ) {
}
private void Adj ( ) {
}
private void Adv ( ) {
}
private void verbe ( ) {
}
public void phrase ( ) {
} // axiome de la grammaire
}
C) Initialisation des données associées à VT
Un ensemble de procédure
de chargement est élaboré afin d’initialiser les contenus
des différents tableaux, ce qui permet de changer aisément
leur contenu.
procedure
Gener_fr.initnom;
begin
tnom[1]:='chat';
tnom[2]:='chien';
end; |
procedure
Gener_fr.initverbe;
begin
tverbe[1]:='poursuit';
tverbe[2]:='aime';
end; |
procedure Gener_fr.initadjectif;
begin
tadjectif[1]:='beau';
tadjectif[2]:='gentil';
tadjectif[3]:='noir';
tadjectif[4]:='blanc';
end; |
procedure Gener_fr.initarticle;
begin
tarticle[1]:='le';
tarticle[2]:='un';
end; |
procedure Gener_fr.initadverbe;
begin
tadverbe[1]:='malicieusement';
tadverbe[2]:='joyeusement';
end; |
Ces cinq procédures sont
appelées dans une procédure générale d’initialisation
de VT tout entier.
procedure Gener_fr.initabl;
begin
initnom;
initarticle;
initverbe;
initadjectif
end; |
Initialisation des contenus
en Java :
void initnom ( )
{
tnom[0] ="chat";
tnom[1] = "chien";
}
|
void
initverbe ( )
{
tverbe[0] = "poursuit";
tverbe[1] = "aime";
}
|
void initadjectif ( )
{
tadjectif[0] = "beau";
tadjectif[1] = "gentil";
tadjectif[2] = "noir";
tadjectif[3] = "blanc";
}
|
void initarticle ( )
{
tarticle[0] = "le";
tarticle[1] = "un";
}
|
void initadverbe ( )
{
tadverbe[0] = "malicieusement";
tadverbe[1] = "joyeusement";
}
|
void initabl ( ){
initnom ( );
initarticle ( );
initverbe ( );
initadjectif ( );
initadverbe ( );
}
|
Nous avons besoin d’une fonction de tirage aléatoire lorsqu’il
se présente un choix à faire entre plusieurs règles,
comme dans la règle 4 :á GV
ñ ¾®á verbe ñ |
á verbe ñá Adv ñoù nous trouvons deux cas de dérivation
possible pour GV : soit á verbe ñ, soit á verbe
ñá Adv ñ. Nous ferons procéder à un choix aléatoire
par le programme entre l’une ou l’autre des dérivations possibles.
Nous construisons une fonction
Alea qui reçoit en entrée un entier indiquant le nombre n
de choix possibles et qui renvoie une valeur aléatoire comprise
entre 1 et n.
Une implantation possible:
Delphi
|
Java
|
function
Gener_fr.Alea(n:integer):integer;
begin
Alea:=trunc(random*100)mod
n+1;
// ou random(n)+1 en TPascal
end; |
private Random ObjAlea = new Random();
int Alea (int n) {
return ObjAlea.nextInt(n);
}
|
D)
Traduction de chacune des règles de G
Nous traduisons en employant
la méthode proposée règle par règle.
REGLE
| 1 :á phrase
ñ¾®á GN ñá GV ñá GN ñ. |
Nous construisons le corps de
la procédure phrase qui est la partie gauche de la règle.
Les instructions correspondent aux appels des procédures GN, GV.
Delphi
|
Java
|
procedure Gener_fr.phrase;
begin
GN;
GV;
GN;
writeln('.')
end; |
void
phrase ( )
{
GN ( );
GV ( );
GN ( );
System.out.println('.') ;
}
|
REGLE
2 :á GN
ñ¾®á Art ñá Adj ñá Nom ñ
3 :á GN
ñ¾®á Art ñá Nom ñá Adj ñ |
Nous traitons ensemble ces deux
règles car elles correspondent à la même procédure
GN. Ici nous avons un tirage aléatoire à faire pour choisir
laquelle des deux dérivations le programme utilisera.
Delphi
|
Java
|
procedure Gener_fr.GN;
begin
if Alea(2)=1
then// pour règle
3
begin
Art;
Nom;
Adj
end
else // pour règle 2
begin
Art;
Adj;
Nom
end
end ; |
void
GN ( )
{
if (Alea(2) ==1) // pour règle
3
{
Art ( );
Nom ( );
Adj ( );
}
else // pour règle 2
{
Art ( );
Adj ( );
Nom ( );
}
}
|
REGLE
| 4 :á GV ñ¾®á verbe ñ |
á verbe ñá Adv ñ |
Dans ce cas nous avons aussi
à faire procéder à un tirage aléatoire afin de
choisir la dérivation á GV ñ¾®á verbe ñ ou
bien la dérivation á GV ñ¾®á verbe ñá Adv ñ.
Delphi
|
Java
|
procedure Gener_fr.GV;
begin
if Alea(2)=1
then // règle < verbe >
Verbe
else
// règle < verbe > < Adv >
begin
Verbe;
Adv
end
end; |
void
GV ( )
{
if (Alea(2) ==1) // règle:
< verbe >
Verbe
( );
else // règl:e < verbe
>< Adv >.
{
Verbe ( );
Adv ( );
}
}
|
Les règles suivantes
étant toutes des règles terminales, elles sont donc traitées
comme le propose la méthode : chaque règle terminale est
traduite par un writeln(a). Lorsqu’il y a plusieurs choix possibles, là
aussi nous procédons à un tirage aléatoire afin d’emprunter
l’une des dérivations potentielles.
REGLE
5 :á Art
ñ¾® le | un
6 :á Nom
ñ¾® chien | chat
7 :á verbe
ñ¾® aime | poursuit
8 :á Adj
ñ¾® blanc | noir | gentil | beau
9 :á Adv
ñ¾® malicieusement | joyeusement |
Delphi
|
Java
|
procedure Gener_fr.Art;
begin
write(tarticle[Alea(2)],'
')
end; |
void Art ( ) {
System.out.print(tarticle[Alea(2)]+' '
) ;
}
|
procedure
Gener_fr.Nom;
begin
write(tnom[Alea(2)],'
')
end;
|
void Nom ( ) {
System.out.print(tnom [Alea(2)]+' '
) ;
}
|
procedure
Gener_fr.Adj;
begin
write(tadjectif[Alea(4)],'
')
end;
|
void Adj ( ) {
System.out.print(tadjectif [Alea(4)]+' '
) ;
}
|
procedure
Gener_fr.Adv;
begin
write(tadverbe[Alea(2)],'
')
end;
|
void Adv ( ) {
System.out.print(tadverbe [Alea(2)]+' '
) ;
}
|
procedure
Gener_fr.Verbe;
begin
write(tverbe[Alea(2)],'
')
end;
|
void Verbe ( ) {
System.out.print(tverbe [Alea(2)]+' '
) ;
}
|
Le programme principal se bornera
à appeler la procédure phrase (l’axiome de la grammaire) à
chaque fois que nous voulons engendrer une phrase. Ci-dessous dans le tableau
de gauche nous listons la classe Gener_fr Delphi comportant toutes les méthodes
précédentes et le programme d'instanciation d'un objet de cette
classe permettant la génération aléatoire de phrases.
A l'identique dans le tableau de droite, nous listons la classe Gener_fr
Java, puis une autre classe principale générant une suite de
phrases aléatoires :
Classe Delphi
|
Java
|
unit
UclassGenerFr
;
interface
const Maxnbmot = 4 ;
type mot =array [1..Maxnbmot] of
string
;
Gener_fr =
class
private
tnom,tadjectif,tarticle,tverbe,tadverbe : mot ;
procedure initnom ;
procedure initverbe ;
procedure initadverbe ;
procedure initadjectif ;
procedure initarticle ;
procedure initabl ;
function Alea(n :integer
) :integer
;
procedure Article ;
procedure Nom ;
procedure Adjectif ;
procedure Adverbe ;
procedure Verbe ;
procedure fin ;
procedure Grp_Nom ;
procedure Grp_Verbal ;
public
constructor Creer ;
procedure phrase ;
end;
implementation
procedure Gener_fr.initnom ; begin
tnom[1] := 'chat';
tnom[2] := 'chien';
end;
procedure Gener_fr.initverbe ; begin
tverbe[1] :=
'poursuit';
tverbe[2] :=
'aime';
end;
procedure Gener_fr.initadverbe ; begin
tadverbe[1] :=
'malicieusement';
tadverbe[2] :=
'joyeusement';
end;
procedure Gener_fr.initadjectif ; begin
tadjectif[1] :=
'beau';
tadjectif[2] :=
'gentil';
tadjectif[3] :=
'noir';
tadjectif[4] :=
'blanc';
end;
procedure Gener_fr.initarticle ; begin
tarticle[1] :=
'le';
tarticle[2] :=
'un';
end;
procedure Gener_fr.initabl ; begin
Randomize ;
initnom ;
initarticle ;
initverbe ;
initadverbe ;
initadjectif
end;
function Gener_fr.Alea(n :integer
) :integer
;
begin
Alea := random(n) + 1 ;
end;
procedure Gener_fr.Article ; begin
write (tarticle[Alea(2)],
' ' )
end;
procedure Gener_fr.Nom ; begin
write (tnom[Alea(2)],
' ' )
end;
procedure Gener_fr.Adjectif ; begin
write (tadjectif[Alea(4)],
' ' )
end;
procedure Gener_fr.Adverbe ; begin
write (tadverbe[Alea(2)],
' ' )
end;
procedure Gener_fr.Verbe ; begin
write (tverbe[Alea(2)],
' ' )
end;
procedure Gener_fr.fin ; begin
writeln ( '.' )
end;
procedure Gener_fr.Grp_Nom ; begin
if Alea(2) = 1 then
begin
Article ;
Nom ;
Adjectif
end
else
begin
Article ;
Adjectif ;
Nom
end
end;
procedure Gener_fr.Grp_Verbal ; begin
if Alea(2) = 1 then
Verbe
else
begin
Verbe ;
Adverbe
end
end;
procedure Gener_fr.phrase ; begin
Grp_Nom ;
Grp_Verbal ;
Grp_Nom ;
fin
end;
constructor Gener_fr.Creer ; begin
initabl ;
end;
end.
|
import
java.util.Random
;
class Gener_fr
{
final int Maxnbmot
=
4
;
private String [ ] tnom
= new String [Maxnbmot] ;
private String [ ] tadjectif
= new String [Maxnbmot] ;
private String [ ] tarticle
= new String [Maxnbmot] ;
private String [ ] tverbe
= new String [Maxnbmot] ;
private String [ ] tadverbe
= new String [Maxnbmot] ;
private Random ObjAlea = new
Random
();
public Gener_fr ( )
{
initabl ( );
}
private void initnom ( )
{
tnom[0] =
"chat";
tnom[1] =
"chien";
}
private void initadjectif ( )
{
tadjectif[0] =
"beau";
tadjectif[1] =
"gentil";
tadjectif[2] =
"noir";
tadjectif[3] =
"blanc";
}
private void initadverbe ( )
{
tadverbe[0] =
"malicieusement";
tadverbe[1] =
"joyeusement";
}
private void initverbe ( )
{
tverbe[0] =
"poursuit";
tverbe[1] =
"aime";
}
private void initarticle ( )
{
tarticle[0] =
"le";
tarticle[1] =
"un";
}
private void initabl ( )
{
initnom ( );
initarticle ( );
initverbe ( );
initadjectif ( );
initadverbe ( );
}
int Alea ( int n )
{
return ObjAlea .nextInt (
n
);
}
private void GN ( )
{
if ( Alea ( 2 ) ==
1
) // pour règle 3
{
Art ( );
Nom ( );
Adj ( );
}
else // pour règle 2
{
Art ( );
Adj ( );
Nom ( );
}
}
private void GV ( )
{
if ( Alea ( 2 ) ==
1
) // règle: < verbe >
Verbe ( );
else // règle: < verbe > < Adv >
{
Verbe ( );
Adv ( );
}
}
private void Art ( )
{
System.out.print (
tarticle[Alea
( 2 ) ] +' '
) ;
}
private void Nom ( )
{
System.out.print (
tnom[Alea
( 2 ) ] +' '
) ;
}
private void Adj ( )
{
System.out.print (
tadjectif[Alea
( 4 ) ] +' '
) ;
}
private void Adv ( )
{
System.out.print (
tadverbe[Alea
( 2 ) ] +' '
) ;
}
private void Verbe ( )
{
System.out.print (
tverbe[Alea
( 2 ) ] +' '
) ;
}
private void fin ( )
{
System.out.println (
' . ' ) ;
}
public void phrase ( )
// axiome de la grammaire
{
GN ( );
GV ( );
GN ( );
fin ( ) ;
}
}
|
Résultats d'exécution avec les deux langages
:
2. C-grammaires et automates à pile de mémoire
Une C-grammaire est une grammaire
de type 2 dans la classification de Chomsky.
Nous adoptons maintenant l’autre
point de vue, " mode analyse " d’une grammaire, pour s’en servir comme
d’un outil de spécification sur la reconnaissance des mots du langage
engendré par cette grammaire. Cette partie est appelée l’analyse
syntaxique. Dans le cas d’une grammaire de type 3, ce sont les automates
d’états finis qui résolvent le problème. Comme ils sont
faciles à faire construire par un débutant, nous les avons
détaillés dans un paragraphe qui leur est consacré spécifiquement.
Dans le cas où G est de type 2 sans être de type 3, nous allons
esquisser la solution du problème en utilisant les automates à
pile sans fournir de méthodes générales sur leur construction
systématique. L’écriture des analyseurs à pile fait
partie d’un cours sur la compilation qu’il n’est donc pas question de développer
auprès du débutant. Il est toutefois possible de montrer à
un étudiant sur des exemples bien choisis et simples que l’on peut
programmer de tels analyseurs.
Nous retiendrons le côté
formateur du principe général de la reconnaissance des mots
d’un langage par un ordinateur, aussi bien par les automates d’états
finis que par les automates à pile. Nous trouverons aussi une application
pratique et intéressante de tels automates dans le filtrage des
données. Enfin, lorsque nous élaborerons des interfaces, la
reconnaissance de dialogues simples avec l’utilisateur sera une aide à
la convivialité de nos logiciels.
2.1 Définition d’un
automate à pile
A = (VT, E, q0, F, µ, Vp, )
où :
E = ensemble des états
(card E est fini)
q0 Î E (q0 , l’état
initial).
E Ì F(F, l’ensemble des états finaux).
VT =Vocabulaire terminal, contient
l’élément #.
Vp = Vocabulaire
de la pile, contient toujours 2 éléments spéciaux(notésw et Nil ).
w Î Vp (symbole initial de pile) et
Nil Î Vp
µ : VT* x E x Vp ® E x Vp’* (fonction de transition de A)
avec : Vp’* = ( VpÈ { # })* ( monoïde
sur VpÈ {#} )
Une transition a donc la
forme suivante :
µ : (aj, qi,a) ® µ(aj, qi,a)=(qk, xn) |
Par rapport à un automate
d’états finis, nous trouvons dans ces automates une pile (genre
LIFO) dans laquelle l’automate va ranger des symboles pendant son
analyse.
2.2 Algorithme de fonctionnement
d’un automate à pile
En pratique, afin de simplifier
les programmes à écrire, nous définirons un vocabulaire
de pile Vp normalisé comme suit:
Vp = Vp ’ = VT È {#} È { w, Nil }
Intérêt de la notion d’automate :
C’est la fonction de transition qui est l’élément
central d'un automate, elle doit être définie de manière
à permettre d’analyser un mot de VT*, et aussi de décider de
l’appartenance ou non d’un mot à un certain langage. Ce langage d’appartenance
est appelé le langage reconnu par l’automate.
|
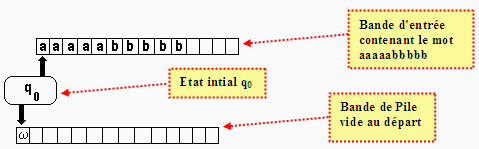
Nous construisons notre automate
à pile comme étant un dispositif physique muni :
- d’une bande d’entrée
(de papier, ou magnétique par exemple) composée de cases ne
pouvant contenir chacune qu’un seul symbole de VT à la fois,
- d'une autre bande de pile
composée de cases ne pouvant contenir chacune qu’un seul symbole
de Vp à la fois,
- de deux têtes
de lecture ou écriture de symobles :
- l'une de lecture capable
de reconnaître des éléments du vocabulaire terminal VT dans chaque case de la bande d'entrée,
et possédant plusieurs états. La tête de lecture se
déplace de gauche à droite d’une case à la fois,
- l'autre tête de
lecture/écriture capable de lire ou d'écrire des éléments
du vocabulaire de pile Vp dans chaque case de la bande de pile,
cette tête se déplace dans les deux sens, mais d'une seule
case à la fois.
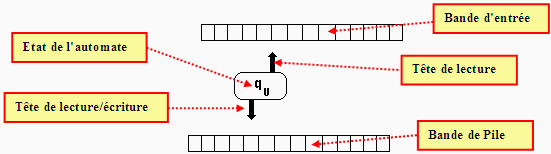 fig - un automate à pile
fig - un automate à pile
- Les règles de transitions
spécifient la manipulation de la bande d'entrée et de la pile
de l'automate.
L’algorithme de fonctionnement d'un tel automate
est le suivant :
On fournit un mot que l’on écrit symbole par symbole de gauche à
droite dans chaque case de l’automate (par exemple avec VT ={a,b} le mot aaaaabbbbb ):
L’automate est mis à l’état initial q0 , sa tête
de lecture d'entrée est positionnée sur la première
case à gauche de la bande d'entrée(1er symbole du mot à
reconnaître), la pile est initialisée avec le symbole w au sommet :
- La tête de lecture
se déplace par examen des règles de transition de l’automate
en y rajoutant l’examen du sommet de la pile. Le triplet (aj, qi,a) enclenche le processus de recherche d’une transition possible
dans la partie gauche de la liste des règles de transitions de µ
(il y a recherche de la transition µ : (aj, qi, a) ¾® ......). Supposons
que la case contienne le symbole aj que la tête soit à
l’état qi , et que le sommet de pile ait pour valeur a :
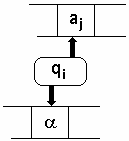
- La transition (aj, qi, a) ¾® (qk , xn) signifie que l’automate
peut passer de l’état qi à l’état qk
à condition que le mot d’entrée débute par la chaîne
préfixe aj élément de VT* (notons que la chaîne aj peut
être réduite par sa définition à un seul élément
de VT , ce qui est généralement
le cas pratique) et que la chaîne a de Vp se trouve en sommet de pile. Le résultat
de la transition fait que le symbole aj est lu et donc reconnu, que la tête
d'entrée pointe vers le symbole suivant de la bande d'entrée,
que le sommet de la pile a été remplacé par la chaîne
xn (donc l'élément xn a été empilé à
la pile), que l'état de l'automate a changé et qu'il vaut
maitenant qk , enfin que la tête de pile pointe sur le nouveau sommet
:
- La transition (aj, qi
, a) ¾® ( qk , Nil ) signifie pour l’automate
de ne rien faire dans la pile. Le résultat de la transition fait
que l'état de l'automate passe de qi à qk et que la tête
d'entrée pointe sur le symbole suivant de la bande d'entrée
:
- la transition (aj , qi,
b) ¾® (qk , # ) signifie effacer l’actuel sommet
de pile et pointer sur l’élément d’avant dans la pile (ce
qui revient à dépiler la pile). Le résultat de la transition
fait que l'état de l'automate passe de qi à qk et que
la tête d'entrée pointe sur le symbole suivant de la bande
d'entrée :
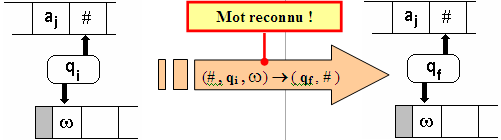
- Le mot est reconnu si
l’automate rencontre une règle de transition de la forme
(# , qi , w) ¾® ( qf
, Nil ), où qf est un état final.
L'automate s’arrête alors :
- Si la recherche de la
transition µ : (aj , qi , ) ......ne donne pas de résultat
on dit que l'auomate bloque : le mot n'est pas reconnu.
Exemple :
E= {e0,e1,e2}
e0 Î E (e0 , état initial)
F ={e2} (F, état final)
VT = {a,b,#}
Vp = {a,b,#,w,Nil}
Règles:
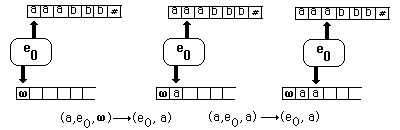
(a , e0, w ) ®(e0, a)
(a , e0, a ) ®(e0, a)
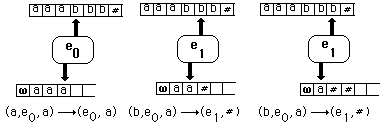
(b , e0, a ) ®(e1, #)
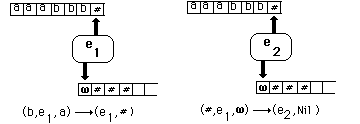
(b , e1, a ) ®(e1, #)
(# , e1, w ) ®(e2, Nil)
Fonctionnement sur un exemple:
reconnaissance du mot aaabbb
Propriété
:
| Un langage est un C-langage
(engendré par une C-grammaire) ssi il est accepté
par un automate à pile. |
L’automate précédent
reconnaît le C-langage L suivant :
L={a...ab...b,n symboles
a concaténés à n symboles b, n ³ 1}
sur l’alphabet VT={a,b}
dont une C-grammaire G est :
VT ={a,b}
VN={S,A}
Axiome: S
Règles :
1 : S ®aSb
2 : S ® ab
2.3 Programme Pascal d’un
automate à pile
 Pascal.Automates
\Pasautopile.pas
Pascal.Automates
\Pasautopile.pas
Ci dessous un petit programme
pascal simulant l’automate précédent :
program automate_a_pile;
{L=aa.(n).abb.(n).b
n>=1 à pile de mémoire}
const
fin=2; omega='$';
non=-1; KNil='@';
type
etat=-1..10;
Vt=char;
Vp=char;
var
q:etat;
mot:string;
numcar,ptrpile:integer;
car:Vp;
pile:array[1..100]of
char;
procedure init_pile;
begin
ptrpile:=1;
pile[1]:=omega;
end;
procedure transition(ai:Vt;qj:etat;alpha:Vp;
var qk:etat;var
beta:Vp);
var
i:integer;
begin
write('(',ai:2,',',qj:2,',',alpha:2,')');
if
(ai='a')and(qj=0)and(alpha=omega) then begin
qk:=0;{ règle ; (a,e0,w) -->(e0,a)
}
beta:='a'
end
else if
(ai='a')and(qj=0)and(alpha='a') then begin
qk:=0; { règle ; (a,e0,a) -->(e0,a) }
beta:='a'
end
else if
(ai='b')and(qj=0)and(alpha='a') then begin
qk:=1; { règle ; (b,e0,a) -->(e1,#) }
beta:='#'
end
else if
(ai='b')and(qj=1)and(alpha='a') then begin
qk:=1; { règle ; (b,e1,a) -->(e1,#) }
beta:='#'
end
else if
(ai='#')and(qj=1)and(alpha=omega) then begin
qk:=fin; { règle ; (#,e1,w) -->(e2,Nil)
}
beta:=KNil
end
else begin
{blocage dans tous les autres cas}
qk:=non;
beta:=KNil
end;
write('-->(',qk:2,',',beta,')
pile=');
for
i:=1 to ptrpile do write(pile[i]:2);
writeln
end;
begin
write('Entrez
un mot: ');
readln(mot);
q:=0;
numcar:=1;
init_pile;
while
(q<>non)and(q<>fin) do
begin
transition(mot[numcar],q,pile[ptrpile],q,car);
numcar:=numcar+1;
if
car='#' then ptrpile:=ptrpile-1
else
if (car='a')or(car='b') then
begin
ptrpile:=ptrpile+1;
pile[ptrpile]:=car
end
end;
if
(q=fin)and(car=KNil) then writeln('Chaîne reconnue !')
else
writeln('Blocage, chaine non reconnue !')
end.
Exécution de ce programme
sur l’exemple précédent aaabbb :

2.4 Programme Delphi d’une classe d'automate à
pile
Nous utilisons une classe de
pile Lifo ClassLifo événementielle, déjà définie
auparavant pour représenter la pile de l'automate. Afin que la pile
Lifo de l'automate gère facilement des éléments de
type string, au lieu de la faire dériver du type List de Delphi,
nous proposons de la dériver du type TStringList qui est une classe
de liste de chaînes :
ClassLifo
= class (TStringList)
private
FOnEmpiler
: DelegateLifo
;
FOnDepiler
: DelegateLifo
;
function getSommet :string ;
public
strPile :string ;
function
Est_Vide
: boolean ;
procedure
Empiler (elt
: string ) ;
procedure
Depiler (
var elt : string ) ;
procedure EffacerPile ;
procedure AfficherPile ;
property
Sommet
:string read getSommet ;
property
OnEmpiler
: DelegateLifo
read FOnEmpiler
write FOnEmpiler
;
property
OnDepiler
: DelegateLifo
read FOnDepiler
write FOnDepiler
;
end;
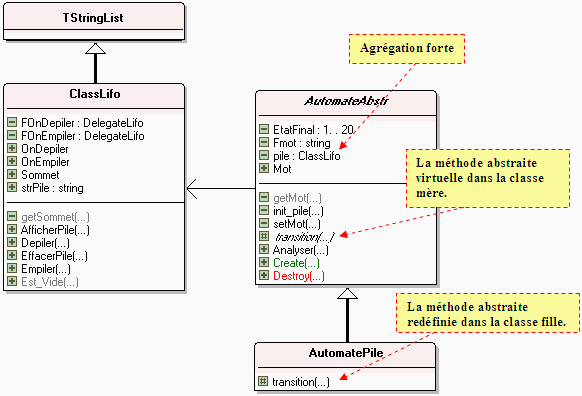
Nous construisons une classe abstraite
d'automate à pile AutomateAbstr qui implante toutes fonctionnalités
d'un automate à pile, mais garde abstraite et virtuelle la méthode
transition qui contient les règles de transitions de l'automate, ceci
afin de déléguer son implementation à chaque classe d'automate
particulier. Chaque classe fille héritant de AutomateAbstr redéfinira
la méthode virtuelle transition.
Code complet de la classe pile de l'automate
unit ULifoEvent
;
interface
uses classes,Dialogs, SysUtils ;
type
DelegateLifo =
procedure ( Sender: TObject
; s :string
) of
object
;
PileVideException =
class (Exception)
end;
ClassLifo =
class
(TStringList)
private
FOnEmpiler :
DelegateLifo
;
FOnDepiler :
DelegateLifo
;
function getSommet :string
;
public
strPile :string
;
function Est_Vide : boolean
;
procedure Empiler (elt : string
) ;
procedure Depiler ( var
elt
: string ) ;
procedure EffacerPile ;
procedure AfficherPile ;
property Sommet :string read
getSommet ;
property OnEmpiler :
DelegateLifo
read FOnEmpiler
write FOnEmpiler
;
property OnDepiler :
DelegateLifo
read FonDepiler
write FOnDepiler
;
end;
implementation
procedure ClassLifo.AfficherPile ;
var i :integer ;
begin
if self.count <>
0
then
for i := 0 to self.Count -
1
do
write (self.Strings[i],
' ' )
;
writeln
end;
procedure ClassLifo.Depiler( var
elt
: string ) ;
begin
if not
Est_Vide
then
begin
elt :=
self.Strings[0]
;
strPile := '';
self.Delete(0) ;
if assigned(FOnDepiler) then
FOnDepiler ( self
,elt )
end
else
raise pilevideexception.create (
'impossible de dépiler: pile vide'
)
end;
procedure ClassLifo.Empiler(elt : string ) ;
begin
self.Insert(0 , elt) ;
if assigned(FOnEmpiler) then
FOnEmpiler ( self
,elt )
end;
procedure ClassLifo.EffacerPile ;
begin
self.Clear ;
end;
function ClassLifo.Est_Vide : boolean
;
begin
result :=
self.Count
=
0
;
end;
function ClassLifo.getSommet : string
;
begin
result :=
self.Strings[0]
end;
end.
Code complet des classes AutomateAbstr et AutomatePile
unit UAutomPile ;
interface
uses ULifoEvent ;
type
etat =- 1..20 ;
Vt =char ;
Vp =char ;
AutomateAbstr =
class
private
EtatFinal :
1..20
;
Fmot :string
;
pile : ClassLifo ;
procedure setMot(s :string
) ;
function getMot :string
;
procedure init_pile ;
protected
procedure transition(ai :
Vt ; qj : etat ; alpha : Vp ; var qk : etat ;
var beta : vp) ;
virtual ;
abstract ;
public
property Mot :string read
getmot write
setMot ;
procedure Analyser ;
constructor Create(fin :integer
) ;
destructor Destroy ;override;
end;
AutomatePile =
class (AutomateAbstr)
protected
procedure transition(ai :
Vt ; qj : etat ; alpha : Vp ; var qk : etat ;
var beta : vp) ;
override;
end;
implementation
{---- AutomateAbstr ----}
const
omega = '$';
non =- 1 ;
knil = '@';
constructor AutomateAbstr.Create(fin :integer
) ;
begin
pile := ClassLifo.Create
;
self.init_pile ;
if fin in
[1..20]
then
EtatFinal :=
fin
else
EtatFinal :=
20 ;
Fmot := '#';
end;
destructor AutomateAbstr.Destroy ;
begin
pile.Free ;
inherited;
end;
function AutomateAbstr.getMot : string
;
begin
result :=
Fmot ;
end;
procedure AutomateAbstr.setMot(s : string
) ;
var long :integer
;
begin
long := length(s) ;
if long <>
0
then
begin
if s[long] <>
'#' then
Fmot := s + '#';
end
else
fmot := '#';
end;
procedure AutomateAbstr.init_pile ;
begin
pile.EffacerPile ;
pile.Empiler(omega) ;
end;
procedure AutomateAbstr.Analyser ;
var
q : etat ;
numcar :integer
;
carPile : Vp ;
s :String ;
begin
q := 0 ;
numcar := 1 ;
init_pile ;
while (q <>
non)
and (q <>
EtatFinal)
do
begin
transition(Fmot[numcar],q,pile.Sommet[1],q,carPile)
;
pile.AfficherPile ;
numcar := numcar + 1 ;
if carPile = '#' then
pile.Depiler(s)
else
if (carpile = 'a' ) or (carpile = 'b' ) then
pile.Empiler(carPile)
;
end;
if (q = etatfinal) and (carpile = knil) then
writeln ( 'chaine reconnue !' )
else
writeln ( 'blocage, chaine non reconnue !'
)
end;
{---- AutomatePile ----}
procedure AutomatePile.transition(ai
: Vt ; qj : etat ; alpha : Vp ;
var qk : etat ;
var beta : vp) ;
begin
write ( '(' ,ai : 2, ',' ,qj : 2, ',' ,alpha : 2, ')' ) ;
if (ai = 'a' ) and (qj = 0) and (alpha = omega) then
begin
qk := 0 ; { règle ; (a,e0,$) -->(e0,a) }
beta := 'a'
end
else
if (ai = 'a' ) and (qj = 0) and (alpha = 'a' ) then
begin
qk := 0 ; { règle ; (a,e0,a) -->(e0,a) }
beta := 'a'
end
else
if (ai = 'b' ) and (qj = 0) and (alpha = 'a' ) then
begin
qk := 1 ; { règle ; (b,e0,a) -->(e1,#) }
beta
:= '#'
end
else
if (ai = 'b' ) and (qj = 1) and (alpha = 'a' ) then
begin
qk := 1 ; { règle ; (b,e1,a) -->(e1,#) }
beta
:= '#'
end
else
if (ai = '#' ) and (qj = 1) and (alpha = omega) then
begin
qk := EtatFinal ;
{ règle ; (#,e1,$) -->(e2,Nil) }
beta := KNil
end
else
begin {blocage dans tous les autres cas}
qk := non ;
beta := KNil
end;
write ( '--(' ,qk : 2, ',' ,beta, ') pile='
) ;
end;
end.
Programme utilisant la classe Automate
|
program
ProjAutomPile
;
{$APPTYPE CONSOLE}
uses
SysUtils,
UAutomPile in
'UAutomPile.pas';
var Automate :
AutomatePile
;
begin
Automate :=
AutomatePile.Create(2)
;
Automate.Mot :=
'aaaaabbbbb';
Automate.Analyser ;
readln ;
end.
|
Exécution de ce programme sur l’exemple
aaaaabaabb :
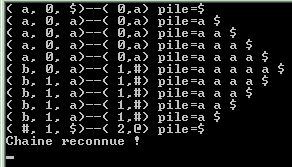
|
La construction générale
et systématique de tous ces automates à pile dépasse
le cadre de ce document.