Plan du chapitre:

1. Quelques mots sur les grammaires

 
1.1 Dérivation à droite et à gauche
1.2 Ensembles First et Init
1.3 Ensemble Follow
1.4 Calcul des Follows à partir des First
1.5 Calcul pour une grammaire arithmétique
1.6 Calcul pour une grammaire du mini-français

2. Grammaire LL(1) pour analyse déterministe

 
2.1 Une condition pratique d’analysabilité LL(1)
2.2 Méthode pratique de vérification
2.3 Une grammaire G_F2 de type LL(1) du mini-français
2.4 Schémas d’algorithmes associés à G_F2

2.5 Procédures pascal associées aux blocs dans G_F2
 
 

---

Bien qu’il ne soit pas dans les objectifs de cet ouvrage de systématiser les méthodes de reconnaissance, nous abordons le sujet sur des cas et des exemples particuliers. L’attitude de systématisation méthodologique et pratique adoptée devrait fournir matière à réflexion et profiter à l’étudiant.

 
1. Quelques mots sur les grammaires

L’expérience a montré qu’un des cas particuliers abordables en initiation est celui où une C-grammaire G possède la propriété d’être analysable par analyse LL(1). Ces analyseurs sont plus simples à construire, et surtout il est possible de systématiser leur construction. Il apparaît que beaucoup de grammaires sont LL(1) et qu’un très grand nombre d’exemples du niveau étudiant débutant peuvent être décrits par une grammaire LL(1). C’est pourquoi nous fournirons plus loin un exemple de génération manuelle d’un petit analyseur de mots du genre LL(1) à partir d’un TAD, ainsi qu’une définition d’une grammaire LL(1).
 
 

1.1 Dérivation à droite et à gauche

Nous dirons par définition que x se dérive le plus à gauche en y et l’on écrira :

x 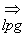 y si et seulement si :

$aÎ(VNÈVT)*  $ ri : A ¾®b    avecA Î VN si x = Aa alors y = ba

Nous dirons par définition que x se dérive le plus à droite en y et l’on écrira :

x 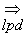 y si et seulement si :

$aÎ(VNÈVT)*  $ ri : A ¾® b    avecA Î VN si x = aA alors y = ab

Comme pour la dérivation, on définit la fermeture transitive de chacune de ces deux relations binaires. Nous les notons :

x 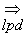 * y et x  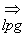* y .
 
 
 

1.2 Ensembles First et Init
 

Nous allons définir quelques ensembles de symboles utiles à une reconnaissance des mots dans une grammaire G, G = (V_N,V_T,S,R).
 

Notations : Les ensembles First et leurs propriétés

Soient (x,y) Î(VNÈ VT)*2, A Î VN (on suppose que A possède dans le cas général plusieurs expansions A ¾® a1 | a2  | ...  | an ), le symbole S est l'axiome de la gramaire G. Nous notons : First(x) ={a Î VT  / x 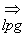 * ay }

Autrement dit pour l’élément a Î First(x) nous avons :
a est un symbole du vocabulaire terminal qui commence les chaînes qui se dérivent de x (e inclus), comme dans x Þ * ab.
 

Enonçons deux propriétés qui vont servir en pratique.

propriété n°1.2.1 :

si aÎ VT*, First(ax) = {a}

propriété n°1.2.2 :

"(x,y) Î  (VN È VT )*2 First(xy) = First(x), sauf dans le cas où x Þ *e , on a alors : First(xy) = First(x) È First(y)

Définition des ensembles Initiaux :
 

Init(A) = 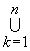 First(ak)  où : ak  est l'une des expansions de A ¾® a1 | a2  | ...  | an convention : si A Î VT, Init(A) = {A}


 

_{Ces ensembles Init(A) permettent de rassembler les symboles terminaux qui se trouvent au début de tout mot dérivé par chacune des expansions de A (A ¾® a1 | ... | an). Nous traitons un exemple complet plus loin.}
 
 

1.3 Ensemble Follow
 

Seulement dans le cas où A Î V_N , on calcule l’ensemble suivant:

Follow(A) = { a Î VT  / S Þ * aAx  (où aÎVT ,et a Î Init(x)) }

Cet ensemble correspond aux symboles qui suivent les mots dérivés de A dans la grammaire. Ce sont les éléments terminaux a Î V_T  apparaissant immédiatement à droite de A dans toutes les chaînes contenant A, comme dans S ÞaAab.

Grâce aux ensembles Init et Follow, nous pouvons dire que nous disposons de deux familles de symboles qui encadrent les mots de la grammaire G. Cette remarque soulève le voile sur une stratégie pratique de reconnaissance des mots engendrés par une grammaire.
 

Enonçons une propriété calculatoire des Follow qui nous servira:

propriété n°1.3.1 :

si       A ¾® aB ,A Î VN,B Î VN, a Î VT* alors   Follow(A) Ì Follow(B)


 
 

1.4 Calcul des Follows à partir des First
 

Soit une C-grammaire G, G = (V_N,V_T,S,R).

Calcul des Follow(A) où A Î V_N  :

Les règles contenant A en partie droite peuvent avoir d’une manière générale deux formes : B ¾®aAb ou B ¾®aA (B Î V_N ).
 

Pour toute règle de la forme B ¾®aAb , (si e Ï First(b)) Follow (A) = Follow(A) È First (b )

Pour toute règle de la forme B ¾®aAb , (si e Î First(b)) et Pour toute règle de la forme B ¾®aA Follow (A) = Follow(A) È Follow(B)

Exemple d’une C-grammaire G :

VT = {a, b}
VN = {A, S}
axiome: S
Règles :
1 : S ¾® aAS
2 : S ¾® b
3 : A ¾® a
4 : A ¾® bSA

On suppose que tous les mots de G se termineront par le symbole spécial ‘#’ de fin de mot.
 

Calcul de Init(S):
il y a 2 expansions de S (Règle 1 et Règle 2)

Init(S) = First (aAS) È First (b)

nous avons : First (b) = {b}
nous avons : First (aAS) = {a}

Donc Init(S) = {a} È {b}
 
 

Calcul de Init(A):
Il y a 2 expansions de A (Règle 3 et Règle 4)

Init(A) = First (a) È First(bSA)

nous avons : First (a) = {a}
nous avons : First (bSA) = {b}

Donc : Init(A) = {a} È {b}
 

conclusion : Init(S) = Init(A) = {a,b}

Passons au calcul des Follow à l’aide des Init.

Calcul de Follow(S):
S est l'axiome de la grammaire d'après la définition:
Follow (S) = {#}

Dans la règle 4 ( A ¾® bSA ) d'après la définition:
Follow (S)ß Follow (S) È Init(A)
 

D'où : Follow(S)={#,a,b}

Calcul de Follow(A):
Initialisation de Follow (A) ß Æ
Dans la règle 4 (S ¾® aAS) d'après la définition :
Follow (A) ß Init(S)
 

D'où : Follow (A) = {a,b}

Nous proposons d’effectuer les calculs précédents sur deux exemples pratiques dont le contenu pourra être réutilisé plus loin.
 
 
 

1.5 Calcul pour une grammaire arithmétique

Reprenons une grammaire G_exp ambiguë des expressions arithmétiques, déjà proposée auparavant :
 

Gexp = (VN,VT,Axiome,Règles) VT ={ 0, ..., 9, +, -, /, *, ), ( } VN = { á Expr ñ, á Nbr ñ, á Cte ñ, á Oper ñ } Axiome : á  Expr ñ Règles : 1 :á  Expr ñ ¾® á  Nbr ñ | (á Expr ñ) | á  Expr ñá  Oper ñá  Expr ñ 2 :á  Nbr ñ ¾® á  Cte ñ | á  Cte ñá  Nbr ñ 3 :á  Cte ñ ¾® 0 | 1 |...| 9 4 :á  Oper ñ ¾® + | - | * | /


 

Calcul des ensembles Init :

Provenant de la règle n°1

á Exprñ ¾®á Nbrñ | (á Expr ñ) | á  Expr ñá  Oper ñá  Expr ñ

Init(Expr) = First(Nbr)È First((Expr))È First(Expr Oper Expr)

Comme Nbr Î V_N  il faut calculer son ensemble Init(Nbr).
First((Expr))={‘(‘} d’après prop.1.2.1
First(Expr Oper Expr)= First(Expr) car e ne dérive pas de Expr.

conclusion :

Init(Expr) = Init(Nbr) È{(}


 

Provenant de la règle n°2

á  Nbr ñ ¾® á  Cte ñ | á  Cte ñ á  Nbr ñ

Init(Nbr) = First(Cte)È First(Cte Nbr)

Comme Cte Î V_N  il faut calculer son ensemble Init(Cte).
First(Cte Nbr)= First(Cte) d’après prop.1.2.2

conclusion :

Init(Nbr) = Init(Cte)


 

Provenant de la règle n°3

á Cte ñ ¾® 0 | 1 |...| 9

Init(Cte) = First(0)È ... È First(9) = {0,1,...,9}


 

Provenant de la règle n°4

á Oper ñ ¾® + | - | * | /

Init(Oper) = First(+)È ... È First(/) = {+,-,*,/}

Récapitulatif

Init(Oper) = {+,-,*,/} Init(Cte) = {0,1,...,9} Init(Nbr) = {0,1,...,9} Init(Expr) = {0,1,...,9,(}


Calcul des ensembles Follow

Calcul de Follow(Expr) :
Nous devons chercher dans toutes les règles de la grammaire celles qui contiennent en partie droite le non terminal Expr. Lorsque dans une règle de la forme " A ¾®a<Expr>b " Expr est en partie droite, en appliquant la définition, nous obtenons le fait que Follow(Expr) contient le First(b). Nous procédons donc ici à un calcul incrémental de l’ensemble Follow(Expr) par adjonctions successives des First qui le composent.
 

Provenant de la règle n°1
(les 2 premières expansions)

á Expr ñ ¾® á Nbr ñ pas de Expr en partie droite. á Expr ñ ¾®(á Expr ñ)

Init(‘)‘)=First(‘)’) Ì Follow(Expr) d’après la définition

(la troisième expansion)

á Expr ñ ¾® á Expr ñ á Oper ñ á Expr ñ

Init(Oper) Ì Follow(Expr) d’après la définition

Il n’y a pas d’autres règles contenant le symbole Expr en partie droite, donc le calcul du Follow(Expr) est terminé :
 

Follow(Expr)= Init(Oper) È Init(‘)‘)= {+,-,*,/,)}


 

Le calcul est identique pour tous les autres follow.

Calcul de Follow(Nbr) :
(examen de toutes les parties droites contenant Nbr)

Provenant de la règle n°1

á Expr ñ ¾® á Nbr ñ d’après prop.1.3.1

Follow(Expr)Ì Follow(Nbr)


 

Provenant de la règle n°2

á Nbr ñ ¾® á Cte ñ á Nbr ñ rien de plus n’est ajouté.

Follow(Expr)Ì Follow(Nbr)

Il n’y a pas d’autres règles contenant le symbole Nbr en partie droite, donc le calcul du Follow(Nbr) est terminé :
 

Follow(Nbr)= Follow(Expr)= {+,-,*,/,)}


 

Calcul de Follow(Cte) :
(examen de toutes les parties droites contenant Cte)

Provenant de la règle n°2

á Nbr ñ ¾® á Cte ñ á Nbr ñ d’après prop.1.3.1

Follow(Nbr)Ì Follow(Cte)


 

Provenant de la règle n°2

á Nbr ñ¾® á Cte ñ á Nbr ñ d’après la définition

Init(Nbr)Ì Follow(Cte)

Il n’y a pas d’autres règles contenant le symbole Cte en partie droite, donc le calcul du Follow(Cte) est terminé :
 

Follow(Cte)= Follow(Nbr) È Init(Nbr)= {+,-,*,/,),0,1...,9}

Calcul de Follow(Oper) :
(examen de toutes les parties droites contenant Oper)

Provenant de la règle n°1

á Expr ñ ¾® á Expr ñ á Oper ñ á Expr ñ d’après la définition

Init(Expr)Ì Follow(Oper)

Il n’y a pas d’autres règles contenant le symbole Oper en partie droite, donc le calcul du Follow(Oper) est terminé :
 

Follow(Oper)= Init(Expr)= { 0,1,...,9,( }


 Récapitulons les Init et les Follow de chaque élément de VN de la grammaire Gexp

Init (Expr) = { 0,1,...,9,( } Init (Nbr) = { 0,1,...,9 } Init (Cte) = { 0,1,...,9 } Init (Oper) = { +, - , * , /  }

Follow (Expr) = { +, - , *, / , ) } Follow (Nbr) =  {+, - , * , / , ) } Follow (Cte) = {+, -, *, /, ), 0, 1, … ,9 } Follow (Oper) = { 0 , 1 , … , 9 , (  }

Rappellons la signification pratique par exemple des ensembles Follow :

Follow (Expr) : Tout mot suivant une expression dérivant de Expr commence par  +, - , *, / , ).
Follow (Cte) : Tout mot suivant une constante dérivant de Cte commence par +, -, *, /, ), 0, 1, … ,9 .
Follow (Oper) : Tout mot suivant un opérateur dérivant de Oper commence par 0 , 1 , … , 9 , (.

Nous pouvons savoir ainsi en consultant ces ensembles si les expressions suivantes sont correctes ou incorrectes dans la grammaire Gexp :

12(5+3) est incorrecte car la parenthèse ouvrante qui est le First de (5+3) n'est pas dans le Follow du nombre 12 (il n'y a pas de parenthèse ouvrante après un nombre).

12*)+2 est incorrecte car la parenthèse fermante qui est le First de )+2 n'est pas dans le Follow de l'opérateur * (il n'y a pas de parenthèse fermante  après un opérateur).

 

1.6 Calcul pour une grammaire du mini-français

Pascal.ProgGramTyp2\Minifr1.pas

Soit G_F1 une grammaire déjà proposée d’un mini-français.

GF1 = (VN,VT,S,R) VT ={le, un, chat, chien, aime, poursuit, malicieusement, joyeusement, gentil, noir, blanc, beau} VN = {áphraseñ, áGNñ, áGVñ, áArtñ, áNomñ, áAdjñ, áAdvñ, áverbeñ} Axiome : áphraseñ Règles : 1 :á phrase ñ¾®á GN ñá GV ñá GN ñ. 2 :á GN ñ¾®á Art ñá Adj ñá Nom ñ 3 :á GN ñ¾®á Art ñá Nom ñá Adj ñ 4 :á GV ñ¾®á verbe ñ | á verbe ñá Adv ñ 5 :á Art ñ¾® le | un 6 :á Nom ñ¾® chien | chat 7 :á verbe ñ¾® aime | poursuit 8 :á Adj ñ¾® blanc | noir | gentil | beau 9 :á Adv ñ¾® malicieusement | joyeusement

Nous livrons ci-après le calcul des ensembles Init et Follow sans le détailler car il s’agit de l’application à cet exemple de la même stratégie utilisée dans le cas de la grammaire précédente. Il est conseillé au lecteur de refaire le calcul lui-même à titre d’entraînement.
 

Calcul des ensembles Init : 

Init(Phrase) = Init(GN)
Init(GN) = Init(Art)
Init(GV) = Init(Verbe)
Init(Art) = {le,un}
Init(Nom) = {chat,chien}
Init(Verbe) = { aime, poursuit }
Init(Adj) = { gentil, noir, blanc, beau }
Init(Adv) = { malicieusement, joyeusement }

Récapitulatif

Init(Phrase) = {le,un} Init(GN) = {le,un} Init(GV) = { aime, poursuit } Init(Art) = {le,un} Init(Nom) = {chat,chien} Init(Verbe) = { aime, poursuit } Init(Adj) = { gentil, noir, blanc, beau } Init(Adv) = { malicieusement, joyeusement }


 Calcul des ensembles Follow :

Follow(Phrase) = {#} fin de chaîne
Follow(GN) = Init(GV) È Init(‘.’) à partir de règle.1
Follow(GV) = Init(GN) à partir de règle.1
Follow(Art) = Init(Adj) È Init(Nom) à partir de règles.2 et 3
Follow(Nom) = Follow(GN) È Init(Adj) à partir de règles.2 et 3
Follow(Verbe) = Follow(GV) È Init(Adv) à partir de règle 4
Follow(Adj) = Follow(GN) È Init(Nom) à partir de règles.2 et 3
Follow(Adv) = Follow(GV) È Init(Adj) à partir de règle 4

 

Récapitulatif

Follow(Phrase) = {#} Follow(GN) = { aime, poursuit, ‘.’ } Follow(GV) = {le,un} Follow(Art) = { gentil, noir, blanc, beau, chat, chien } Follow(Nom) = { gentil, noir, blanc, beau, aime, poursuit } Follow(Verbe) = { le, un, malicieusement, joyeusement } Follow(Adj) = { aime, poursuit, chat, chien, ’.’ } Follow(Adv) = {le,un}

Voyons maintenant comment nous pouvons utiliser pratiquement ces ensembles Follow et Init (ou First) et dans quel cadre s’en servir. Le support de stratégie se dénomme l’analyse LL(1). Nous décortiquons dans le paragraphe suivant un exemple complet en soulignant les aspects méthodologiques généraux sous-jacents.
 
 
 

2. Grammaire LL(1) pour analyse déterministe
 

Les ensembles Init et Follow précédemment étudiés présentent un intérêt pratique dans l’analyse de mots d’une C-grammaire d’un " bon type ". C’est en vue d’une construction ultérieure systématique du filtrage du dialogue homme-machine que nous les avons présentés. En outre ils pourront aussi, comme nous le verrons lorsque nous aborderons ce thème, diriger notre programmation par plans d’action dans le guidage d’une saisie sur une interface. Dans le cas de dialogue avec l’utilisateur, c’est le concepteur du logiciel qui prévoit le  " genre " de dialogue. Donc s’il dispose d’un outil rapide d’analyse du dialogue, il pourra dans la majorité des cas essayer d’élaborer une grammaire analysable rapidement sans alourdir sa tâche de programmation.

Nous avons choisi de présenter la technique la plus simple pour reconnaître les mots d’un langage dans le cas où la C-grammaire est de type LL(1).

La stratégie générale que nous adoptons est la suivante :
A chaque analyse du symbole en cours, il nous suffira de " regarder " le symbole suivant. Si la grammaire s’y prête (et nous allons donner les propriétés de telles grammaires), nous pourrons connaître à l’avance l’ensemble de tous les symboles (tous différents)pouvant se trouver après le symbole analysé. Chacun des symboles conduira à une branche d’analyse différente, le procédé est donc déterministe.

Une bonne C-grammaire qui se prête à ce genre d’analyse est dite analysable par la technique LL(1) ou plus brièvement appelée grammaire LL(1).

Nous possédons un mécanisme de construction d’analyseur de mots avec les automates d’états finis pour les grammaire de type-3. Le procédé LL(1) est un outil simple mais suffisamment intéressant pour fournir un cadre méthodique et introductif à d’autres développements. Avec cet outil de nombreux exemples efficaces et non triviaux peuvent être construits et programmés au niveau de l’initiation.

 
 

2.1 Une condition pratique d’analysabilité LL(1)

Nous donnons une condition nécessaire et suffisante posée comme définition pour qu’une C-grammaire soit LL(1). Cette CNS est un énoncé constructif qui va nous servir à vérifier rapidement si nous avons une grammaire LL(1) ou non.

CNS-LL1 :

"A Î VN , A ¾® a1| a2  |.....| an  " (i,j)/ i ¹ j : Init(ai) Ç Init(aj)=Æ  si ak Þ* e alors    " i / i ¹ k , Init(ai) Ç Follow(A) = Æ

 

2.2 Méthode pratique de vérification

Afin de savoir si une C-grammaire donnée est LL(1) et pour appliquer la CNS précédente, nous construisons une table regroupant toutes les informations sur les Init et les Follow de chaque élément du vocabulaire auxiliaire de la grammaire.

Soient A ¾® X1 |...| Xn toutes les expansions de A, A Î V_N. Nous construisons le tableau suivant pour chaque élément A Î V_N :
 




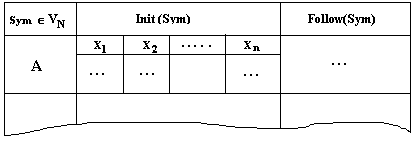
Où chaque colonne identifiée par Xk contient tous les symboles de l’ensemble First(Xk).
 

Puis, à l’aide de ce tableau, nous appliquons la CNS-LL1 :

• Pour un A, A Î V_N fixé, les contenus de chacune des colonnes Xk ne doivent pas avoir d’éléments communs.
• Si une expansion Xk de A se dérive en e (Xk Þ*e), les contenus de toutes les autres colonnes Xp (p ¹ k)ne doivent pas avoir d’éléments commun avec Follow(A).


Ci-après, les tables construites à partir des deux calculs précédents sur la grammaire des expressions arithmétiques et celle du mini-français :
 

	Init					Follow
Expr	0,...,9	(			0,...,9	+ , * , -, /, )
Nbr	0,...,9					+ , * , -, /, )
Cte	0,...,9					+, *, -, /, ), 0,...,9
Oper	+ , * , -, /					0,..., 9, (

Voyons enfin comment les outils que nous venons de considérer peuvent servir en programmation de l'analyse de phrases.

 

2.3 Une grammaire LL(1) du mini-français

Pascal.ProgGramTyp2\Minifr2.pas
 

Voici G_F2 une grammaire LL(1) obtenue à partir de G_F1 par changement des règles selon l’idée de transformation précédente. Nous avons ajouté deux nouveaux symboles dans V_N: <LeNom> et <Suite>
 

GF2 = (VN,VT,S,R) VT ={le, un, chat, chien, aime, poursuit, malicieusement, joyeusement, gentil, noir, blanc, beau} VN = {áphraseñ, áGNñ, áGVñ, áArtñ, áNomñ, áAdjñ, áAdvñ, áverbeñ, áLeNomñ, áSuiteñ} Axiome : áphraseñ Règles : 1 :á phrase ñ¾®á GN ñá GV ñá GN ñ. 2 :á GN ñ¾®á Art ñá LeNom ñ 3 :á LeNom ñ ¾®á Adj ñá Nom ñ | á Nom ñá Adj ñ 4 :á GV ñ ¾®á verbe ñá Suite ñ  5 :á Suite ñ ¾®á GN ñ | á Adv ñá GN ñ 6 :á Art ñ¾® le | un 7 :á Nom ñ¾® chien | chat 8 :á verbe ñ¾® aime | poursuit 9 :á Adj ñ¾® blanc | noir | gentil | beau 10 :á Adv ñ¾® malicieusement | joyeusement

En calculant comme précédemment les Init et les Follow, nous obtenons le tableau récapitulatif suivant:
 

	Init				Follow
Phrase	le, un				#
GN	le, un			aime, poursuit, ‘.’
LeNom	blanc,noir,gentil,beau		chien, chat	aime, poursuit, ‘.’
GV	aime,  poursuit			‘.’
Suite	le, un	malicieusement, joyeusement		‘.’
Art	le, un				blanc, noir, gentil, beau, chat, chien
Nom	chien, chat				blanc, noir, gentil, beau, aime, poursuit, ‘.’
Verbe	aime, poursuit				le,un,malicieusement, joyeusement
Adj	blanc,noir,gentil,beau				aime, poursuit, chat, chien, ‘.’
Adv	malicieusement, joyeusement				le, un

ci-dessus un tableau pour la grammaire G_F2
 

Elle vérifie la CNS-LL1, cette grammaire G_F2 est LL(1).

Nous indiquons ensuite un moyen destiné à effectuer la reconnaissance manuelle tout d’abord, puis par programme pascal, uniquement dans le cas de la grammaire LL(1) G_F2 du mini-français. Cela pourra inciter l’étudiant à aller chercher dans les ouvrages spécialisés les méthodes générales mettant en œuvre ces techniques de reconnaissance.
 
 

• un outil nommé " Symsuivant " qui met le prochain symbole de la phrase dans " SymLu ",
• un outil " Erreur " de signalement d’erreur dès qu’une erreur d’analyse est détectée. L’outil " Erreur " arrête en même temps tout le processus de reconnaissance.

  Pascal.ProgGramTyp2\Analyfr2.pas

Afin de clore cette ouverture sur la reconnaissance, nous traduisons en pascal les spécifications précédentes sur les blocs d’analyse. A chaque bloc d’analyse nous faisons correspondre une procédure pascal en nous inspirant des choix effectués lors de l’écriture d’un générateur de phrase du mini-français.
 

Les structures de données :

Nous disposons d’un type liste obtenu à partir d’une unité de liste linéaire de chaînes.

Le type liste sert à stocker des éléments de V_T qui sont tous des string.
 

Pascal.ProgGramTyp2\UListchn.pas

var
tnom,tadjectif,tarticle,tverbe,tadverbe:liste;
{toutes ces listes contiennent les symboles de V_T }

Init_Grp_Nom, Init_LeNom, Init_Grp_Verbal,Init_Suite:liste;
{toutes ces listes contiennent les symboles des Init}

Symlu:string; {le symbole lu}
PhraseLue,Copiephrase:string; {la phrase à analyser et sa copie}

  Les outils de base :

procedure Symsuiv(var Sym:string);
{l’outil Symsuivant, le paramètre Sym
contient le symbole extrait}
begin
 if Copiephrase<>'' then
  if Copiephrase='.' then Sym:='.'
  else
  begin
   Sym:=copy(Copiephrase,1,pos(' ',Copiephrase)-1);
   delete(Copiephrase,pos(Sym,Copiephrase),length(sym)+1)
  end;
end;

procedure Erreur;
{outil Erreur}
begin
 writeln('Erreur');
 readln ;
 halt
end;

function AppartientA(Sym:string;Ensemble:liste):boolean;
{teste l’appartenance à un Init donné du symbole Sym }
begin
 AppartientA:=False;
 if Test (Ensemble,Sym) then AppartientA:=True
end;
 
 
 

Traduction de chacun des blocs d’analyse

procedure Nom; {Bloc Analyser Nom}
begin
 if AppartientA(Symlu,tnom) then
  symsuiv(Symlu);
end;

procedure Adjectif; {Bloc Analyser Adj}
begin
 if AppartientA(Symlu,tadjectif) then
  symsuiv(Symlu);
end;

procedure Adverbe; {Bloc Analyser Adv}
begin
 if AppartientA(Symlu,tadverbe) then
  symsuiv(Symlu);
end;

procedure Verbe; {Bloc Analyser Verbe}
begin
 if AppartientA(Symlu,tverbe) then
  symsuiv(Symlu);
end;

procedure LeNom; {Bloc Analyser LeNom }
begin
 if AppartientA(Symlu,tadjectif) then
 begin
  Adjectif;
  if AppartientA(Symlu,tnom) then
   Nom
  else erreur
 end
 else
 if AppartientA(Symlu,tnom) then
 begin
  Nom;
  if AppartientA(Symlu,tadjectif) then
   Adjectif
  else erreur
 end
 else erreur
end;

procedure Grp_Nom; {Bloc Analyser GN}
begin
 if AppartientA(Symlu,tarticle) then
 begin
  Article;
  if AppartientA(Symlu, Init_LeNom) then
   LeNom
  else erreur
 end
 else erreur;
end;

procedure Suite; {Bloc Analyser Suite}
begin
 if AppartientA(Symlu,Init_Grp_Nom) then
  Grp_Nom
 else
 if AppartientA(Symlu,tadverbe) then
 begin
  Adverbe;
  if AppartientA(Symlu,Init_Grp_Nom) then
   Grp_Nom
  else erreur
 end
 else erreur
end;

procedure Grp_Verbal; { Bloc Analyser GV }
begin
 if AppartientA(Symlu,tverbe) then
 begin
  Verbe;
  if AppartientA(Symlu,Init_Suite) then
   Suite
  else erreur
 end
 else erreur
end;

procedure phrase; {Bloc Analyser Phrase }
begin
 if AppartientA(Symlu,Init_Grp_Nom) then
 begin
  Grp_Nom;
  if AppartientA(Symlu,Init_Grp_Verbal) then
  begin
   Grp_Verbal;
   if Symlu <>'.' then erreur
   else writeln('Phrase reconnue !')
  end
  else erreur
 end
 else erreur;
end;