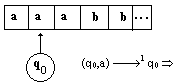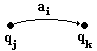3.3.AUTOMATES et GRAMMAIRES

de type 3

---

Plan du chapitre:

1. Automate pour les grammaires de type 3

 
1.1 Automates d’états finis déterministes ou non
1.2 Algorithme de fonctionnement d’un AEFD
1.3 Utilisation d’un AEF en reconnaissance de mots
1.4 Graphe d’un automate déterministe ou non
1.5 Matrice de transition : dans le cas déterministe

2. Grammaires et automates

 
2.1 Automate associé à une K-grammaire
2.2 Grammaire associée à un Automate

 

3. Implantation d'un AEFD en pascal

 
3.1 Fonction de transition à partir des règles
3.2 Fonction de transition à partir de la matrice
3.3 Exemple : les identificateurs pascal-like
• Détermination d’une grammaire G_id adéquate
• Construction de l’automate associé à G_id
• Programme associé à l’automate
3.4 Exemple : les constantes numériques
• Détermination d’une grammaire G_cte adéquate
• Construction de l’automate associé à G_cte
• Programme associé à l’automate

 

---

1. Automates pour les grammaires de type 3

 
Dans ce chapitre, le point de vue adopté est celui de l’implantation pratique des notions proposées en pascal. La reconnaissance automatique et méthodique est très aisément accessible dans le cas des grammaires de type 3 à travers les automates d’états finis. Nous fournissons les éléments théoriques appuyés sur des exemples pratiques.
 
 

1.1 Automates d’états finis déterministes ou non

 
Définition

C’est un Quintuplet A = (VT,E,q0,F,µ)où : VT : vocabulaire terminal de A. E : ensemble des états de A ; E = {q0,q1,...,qn } q0 Î E est dénommé état initial de A. F Ì E : F est l’ensemble des états finaux de A. µ : E x VT ¾®E , une fonction de transition de A.

Définition

Un automate A, A = (VT,E,q0,F,µ), est dit déterministe, si sa fonction de transition µ est une vraie fonction au sens mathématique. Ce qui revient à dire qu’un couple de E x VT n’a qu’une seule image par µ dans E.

Intérêt de la notion d’automate :

Comme pour les automates à pile, c'est la fonction de transition qui est l’élément central de l’automate A. Elle doit être définie de manière à permettre d’analyser un mot de V_T^*, et aussi de décider de l’appartenance ou non d’un mot à un certain langage. Ce langage d’appartenance est appelé le langage reconnu par l’automate.

Exemple : Soit un automate possédant parmi ses règles, les trois suivantes
( q_i , a_j ) ¾®q_k¹
( q_i , a_j ) ¾®q_k²
................
( q_i , a_j ) ¾®q_kⁿ

Il existe trois règles ayant la même partie gauche ( qi , aj ), ce qui revient à dire que le couple ( qi , aj ) a trois images distinctes, donc l'automate est non déterministe.


Par la suite, pour des raisons de simplification pratique, nous considérerons les Automates d’Etats Finis normalisés que nous nommerons AEF, en posant :

F = { q_f } un seul état final
V_T = V_T È{ # } on ajoute dans V_T un symbole terminal de fin
de mot #, le même pour tous les AEF.


1.2 Algorithme de fonctionnement d’un AEF


Nous construisons notre AEF comme étant un dispositif physique muni :


• d’une bande d’entrée (de papier, ou magnétique par exemple) composée de cases ne pouvant contenir chacune qu’un seul symbole de V_T à la fois,

• d'une seule tête de lecture de symobles capable de reconnaître des éléments du vocabulaire terminal VT dans chaque case de la bande d'entrée, et possédant plusieurs états. La tête de lecture se déplace de gauche à droite d’une case à la fois,

fig - un automate d'états finis

• Les règles de transitions spécifient la manipulation de la bande d'entrée de l'automate.


L’algorithme de fonctionnement d'un AEF :

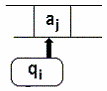
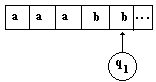
L'algorithme est très semblable à celui d'un automate à pile (en fait on peut considérer qu'il s'agit d'un cas particulier d'automate à pile dans lequel on n'effectue jamais d'action dans la pile), on fournit un mot que l’on écrit symbole par symbole de gauche à droite dans chaque case de l’automate (par exemple avec V_T ={a,b} le mot aaaaabbbbb):

 

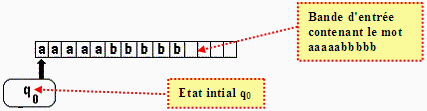
• La tête de lecture se déplace par examen des règles de transition de. Le couple (aj, qi) enclenche le processus de recherche d’une transition possible dans la partie gauche de la liste des règles de transitions de µ (il y a recherche de la transition µ : (aj , qi ) ¾® ......).Supposons que la case contienne le symbole aj que la tête soit à l’état qi :

• La transition ( qi , aj ) ¾® qk  signifie que l’automate peut passer de l’état qi à l’état qk à condition que le mot d’entrée débute par la chaîne préfixe aj élément de V_T* (notons que la chaîne aj peut être réduite par sa définition à un seul élément de V_T , ce qui est généralement le cas pratique. Le résultat de la transition fait que le symbole aj est lu et donc reconnu, que la tête d'entrée pointe vers le symbole suivant de la bande d'entrée :

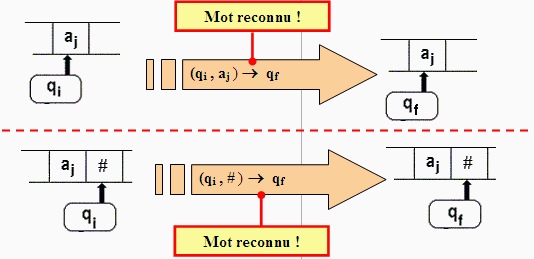
• Le mot est reconnu si l’automate rencontre une règle de transition de la forme ( qi , aj ) ¾® qf   ou bien (qi , # ) ¾®  qf  où qf est un état final. L'automate s’arrête alors. 

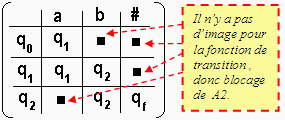
• Si l’AEF ne trouve pas de règle de transition commençant par ( qj , ai ), c’est à dire que le couple ( qj , ai ) n’a pas d’image par la fonction de transition µ, on dit alors que l’automate bloque : le mot n’est pas reconnu comme appartenant au langage.

1.3 Utilisation d’un AEF en reconnaissance de mots

 
Soit la grammaire G₁ déjà étudiée plus haut :
Le langage engendré par G₁ est L(G₁) = { aⁿb^p / (n ³ 1) et (p ³ 1) }

G₁ : V_N = {S,A}
V_T = {a,b}
Axiome : S
Règles
1 : S ¾® aS
2 : S  ¾®aA
3 : A ¾®bA
4 : A ¾®b

Soit l’automate A₁ : ( A₁ est non déterministe )
V_T = {a,b}
E = {q₀,q₁,qf }
µ : ( q₀, a ) ¾® q₀
µ : ( q₀, a ) ¾® q₁
µ : ( q₁, b ) ¾® q₁
µ : ( q₁, b ) ¾® q_f

Fonctionnement pratique de cet AEF  sur le mot a³b² (aaabb) :


 


 
 

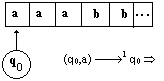
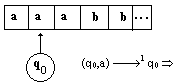
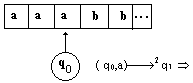
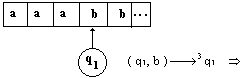
( q1, b ) ¾®4 qf  règle 4  Þ l’AEF s’arrête, le mot aaabb est reconnu !

Vous remarquerez que dans le cas de cet AEF, il nous a fallu aller " voir " un symbole plus loin, afin de déterminer la bonne règle de transition pour mener jusqu’au bout l’analyse.

On peut montrer que tout AEF non déterministe peut se ramener à un AEF déterministe équivalent. C’est pourquoi nous ne considérerons par la suite que les AEF déterministes (notés AEFD).

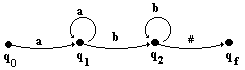
Voici à titre d’exemple un AEFD équivalent à l’AEF A₁ précédent : 

AEFD A₂ reconnaissant le langage { aⁿb^p / (n ³ 1) et (p ³ 1) }

V_T = {a,b,#}
E = {q₀,q₁, q₂,qf }
µ : ( q₀, a ) ¾® q₁
µ : ( q₂, b ) ¾® q₂
µ : ( q₁, a ) ¾® q₁
µ : ( q₂, # ) ¾® q_f
µ : ( q₁, b ) ¾® q₂

Voici la reconnaissance automatique du mot a³b² par cet automate :

( q₀, a ) ¾® q₁
( q₁, a ) ¾® q₁
( q₁, a ) ¾® q₁
( q₁, b ) ¾® q₂
( q₂, b ) ¾® q₂
( q₂, # ) ¾® q_f mot reconnu !
 
 

1.4 Graphe d’un automate déterministe ou non

C’est un graphe orienté, représentant la suite des transitions de l’automate comme suit :

(q_j,a_i) ¾® q_k est représentée par l’arc à 2 sommets :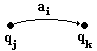 
 

Exemples de graphe des deux AEF précédents :
 

graphe de A1 :

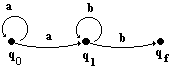
graphe de A2 :

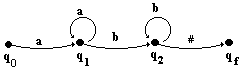
Que l’AEF soit déterministe ou non, il est toujours possible de lui associer un tel graphe.

Exemple :séparer des chiffres et des lettres

Voici un Automate d’Etats Finis Déterministe qui reconnaît :

- les identificateurs Pascal,
- les constantes chiffrées,
- les mots clefs : END , ELSE

Par la suite, afin de ne pas surcharger le graphisme, nous noterons :
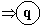l’état initial de l’automate, et  l’état final.
 

Représentons son graphe :



On peut voir dans le dernier exemple le schéma général d’un analyseur lexical qui constitue la première étape d’un compilateur. Il suffit dès que le symbole a été reconnu donc à partir d’un état final f1 ou bien f2 de repartir à l’état 0.
 
 

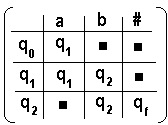
1.5 Matrice de transition : dans le cas déterministe

On représente la fonction de transition par une matrice M dont les cellules sont toutes des états de l’AEF (ensemble E), où les colonnes contiennent les éléments de V_T (symboles terminaux), les lignes contiennent les états (éléments de E sauf l’état final q_f). La règle (q_j,a_i) ¾® q_k est stockée de la façon suivante M(i,j)= q_k où :

la ligne j correspond à l’état q_j
la colonne i correspond au symbole a_i

Exemple : la matrice des transitions de A₂ :
 

Utilisation pratique de la matrice des transitions :
Dénommons Mat[i,j] l’état valide de coordonnées (i,j) dans la matrice des transitions d’un AEFD. Un schéma d’algorithme de reconnaissance par l’AEFD est très simple à décrire :
 

Etat ¬ q0 ; Symlu ¬ premier symbole du mot ; tantque Etat ¹ qf Faire  Etat ¬ Mat[Etat,Symlu] ;  Symlu ¬ Symbole suivant Fintant ;


 
 
 

Correspondance entre grammaire de type 3 et AEF (Automate d’Etats Finis)

2. grammaires et automates
 
 

Autmdelf.dif
 

Il existe une correspondance bijective entre les K-grammaires (grammaires de type-3) et les AEF. Cette correspondance est la base sur laquelle nous sytématisons l’implantation d’un AEFD. En voici une construction pratique .
 
 

2.1 Automate associé à une K-grammaire

Soit G une K-grammaire , G = (V_N,V_T,S,R)
On cherche l’AEF A, A = (V_T^’, E, q₀, q_f, µ), tel que A reconnaisse G.
Soit la constructionsuivante de l'AEF A :
 

1 ) VT’ = VT È {#} 2 ) Chaque élément de VN est un qj de E ( E = VN È {qf} ) 3 ) A toute règle terminale de G de la forme Aj ¾® ak, on associe la règle de transition (qj, ak) ¾® qf 4 ) q0 = S (l’axiome de G) 5 ) A toute règle non terminale de G de la forme Aj ¾® ak Ai, on associe la règle de transition (qj, ak) ¾® qi

L’automate A ainsi construit reconnaît le langage engendré par G.
 

Remarque :

L’automate A1 reconnaissant le langage {anbp /(n³ 1)et(p³ 1) }associé à la grammaire G1 (cf. plus haut) a été construit selon cette méthode.

Exemple : soit G la K-grammaire suivante

G = (V_N,V_T,S,R)
V_T = { a, b, c, # }
V_N = { S, A, B }
Axiome : S
Règles de G :
1 : S ¾® aS
2 : S ¾® bA
3 : A ¾® bB
4 : B ¾® cB
5 : B ¾® #

Soit Aut l’automate associé par le procédé bijectif précédent :
 

Aut = (VT’, E, q0, qf, µ) VT’ = VT S est associé à : q0 A est associé à : q1 B est associé à : qf 1 : S ¾® aS est associé à :( q0, a ) ¾® q0 2 : S ¾® bA est associé à :( q0, b ) ¾® q1 3 : A ¾® bB est associé à :( q1, b ) ¾® q2 4 : B ¾® cB est associé à :( q2, c ) ¾® q2 5 : B ¾® # est associé à :( q2, # ) ¾® qf


 
 
 

2.2 Grammaire associée à un Automate

Soit l’AEF A,  tel que A = ( V_T^’, E , q₀ , q_f ,µ )
On cherche G une K-grammaire du langage reconnu par cet automate.

3. Implantation d’un AEFD en Delphi
 

Nous proposons deux constructions différentes de la fonction de transition d’un AEFD soit en utilisant directement les règles de transition, soit à partir de la matrice de transition.
 

3.1 Fonction de transition à partir des règles

 
Méthodologie

Toute règle est de la forme (qj, ak) ¾® qi , donc nous pourrons prendre comme modèle d’implantation de la fonction de transition une méthode function d'une classe que nous nommerons AutomateEF, dont voici ci-dessous une écriture fictive pour une seule règle..


 

function AutomateEF.transition(q:T_etat;car:Vt):T_etat ; begin  if (q= qj)and(car= ak) then q:= qi {la règle (qj, ak) ¾® qi}  else .... end ;

Toutes les autres règles sont implantées dans la méthode transition de la même façon.
 
L’appel de la méthode transition se fera à travers un objet AEFD de classe AutomateEF :



EtatApres := AEFD.transition(qj, ak) ; {la fonction renvoie l’état qi}


 

Exemple : l’automate déterministe A’₂ ( reconnaissant le langage aⁿb^p )
( en pascal de base Pascal.Automates \aefd_1.pas  )


Code Delphi :

const
   imposs =- 1 ;
   fin = 20 ;
   finmot = '#';
 type
   T_etat = imposs..fin ;
   Vt =char ;
   ....
  AutomateEF  =  class
   q  :  T_etat ;
   mot :string ;
  function  transition(q : T_etat ; car : Vt) : T_etat ; 
end;

Implementation
 
 function  AutomateEF.transition(q : T_etat ; car : Vt) : T_etat ;
  {par les règles de transition :}
  begin
  if  (q = 0) and (car = 'a' )  then    q := 1  {(q0,a) ¾® q1}
   else
   if  (q = 1) and (car = 'a' )  then     q := 1  {(q1,a) ¾® q1}
    else
    if  (q = 1) and (car = 'b' )  then      q := 2  {(q1,b) ¾® q2}
     else
     if  (q = 2) and (car = 'b' )  then       q := 2  {(q2,b) ¾® q2}
      else
      if  (q = 2) and (car = finmot)  then        q := fin  {(q2,#) ¾® qf}
       else
        q := imposs ;  {blocage, le caractère n'est pas dans vt}
   transition := q
  end; 

Appel de la méthode transition dans le programme principal  :

{Analyse}

numcar := 1 ; 
etat := 0 ; 
 while  (etat <> imposs) and (etat <> fin)  do 
 begin 
   Symsuiv(numcar,symlu) ;  {fournit dans symlu le symbole suivant} 
   etat :=  AEFD.transition(etat,symlu) ; 
 end; 

Comme l’automate est déterministe, il est possible de procéder différemment en utilisant sa matrice de transition, ce qui est un bon exemple d’application de la notion de matrice dans un programme.
 
 

3.2 Fonction de transition à partir de la matrice

Méthodologie

UUne autre écriture d’un même AEFD est obtenue (lorsque cela est possible en place mémoire) à partir d’un tableau Delphi (dénoté table) représentant la matrice des transitions de l’automate. Nous utilisons le même modèle d’implantation de la fonction de transition que dans le cas d'une description par règles ( méthode function d'une classe AutomateEF).

Version réduite initiale du code : morceaux de code 

 const 
   imposs =- 1 ; 
   fin = 20 ; 
   finmot = '#'; 
 type 
   T_etat = imposs..fin ; 
   Vt =char ; 
   T_transition =array [T_etat, char ]  of  T_etat ;
  
   AutomateEF  =  class
   q  :  T_etat ; 
   mot :string ; 
   table : T_transition ;  {matrice des transitions} 
end;

Il est nécessaire d’initialiser la matrice table avec les valeurs de départ de l’AEFD. Une méthode init_table pourra se charger de ce travail. Dans ce cas, la méthode transition est très simple à écrire, elle se résume à parcourir la matrice des transitions accessible comme champ de la classe :

Version augmentée du code : morceaux de code 

const 
   imposs =- 1 ; 
   fin = 20 ; 
   finmot = '#'; 
 type 
   T_etat = imposs..fin ; 
   Vt =char ; 
   T_transition =array [T_etat, char ]  of  T_etat ;
  
   AutomateEF  =  class
   q  :  T_etat ; 
   mot :string ; 
   table : T_transition ;  {matrice des transitions} 
   procedure  init_table ;
  function  transition(q : T_etat ; car : Vt) : T_etat ;
end;

implementation
 
 procedure  AutomateEF.init_table ; 
  {initialisation de la table des transitions} 
 
  var 
   i : T_etat ; 
   j : 0..255 ; 
   k :char ; 
  begin  {init_table}
    for  i := imposs  to  fin  do 
    for  j := 0  to  255  do 
      Chargementde(table) 
   ...... 
   end;  {init_table}
  
  function  AutomateEF.transition(q : T_etat ; car : Vt) : T_etat ; 
  {par la table de transition : Dans ce cas, la function transition
  est très simple à écrire. Elle se    
  résume à parcourir la matrice des
  transitions accessible comme champ de la classe
  } 
  begin 
   q  :=  table[q,car] ; 
  result  :=  q ; 
 end; 



L’appel de la méthode transition se fait comme dans le cas précédent, à travers un objet AEFD de classe AutomateEF :

EtatApres := AEFD.transition(qj, ak) ; {la fonction renvoi l’état qi }

Exemple : le même automate (reconnaissant le langage aⁿb^p )

( en pascal de base Pascal.Automates \aefd_2.pas )

Nous reprenons l’automate du paragraphe précédent, mais en l’implantant grâce à sa table de transition.

la méthode transition de l’automate déterministe A2 :   ( reconnaissant le langage anbp )

Morceaux de code Delphi : 

const 
   imposs =- 1 ; 
   fin = 20 ; 
   finmot = '#'; 
 type 
   T_etat = imposs..fin ; 
   Vt =char ; 
   ....
  AutomateEF =  class
 private
   EtatFinal  :  T_etat ; 
   Fmot :string ; 
   table : T_transition ;  {matrice des transitions} 
   procedure  init_table ;
  function  transition(q : T_etat ; car : Vt) : T_etat ;
end;

Implementation
 
 procedure  AutomateEF.init_table ; 
  {initialisation de la table des transitions} 
  var 
   i : T_etat ; 
   j : 0..255 ; 
   k :char ;
  begin  {init_table}
    for  i := imposs  to  fin  do 
    for  j := 0  to  255  do 
      table[i,chr(j)] := imposs ;
    {par défaut tout est non reconnu} 
    table[0, 'a' ] := 1 ; 
    table[1, 'a' ] := 1 ; 
    table[1, 'b' ] := 2 ; 
    table[2, 'b' ] := 2 ; 
    table[2,finmot] := EtatFinal
 end;  {init_table}

  function  AutomateEF.transition(q : T_etat ; car : Vt) : T_etat ; 
  {par la table de transition :} 
  begin 
   q  :=  table[q,car] ; 
  result  :=  q ; 
 end;

Appel de la méthode transition dans le programme principal : 

{Analyse}

numcar := 1 ; 
etat := 0 ; 
 while  (etat <> imposs) and (etat <> fin)  do 
 begin 
   Symsuiv(numcar,symlu) ;  {fournit dans symlu le symbole suivant} 
   etat :=  AEFD.transition(etat,symlu) ; 
 end; 

La unit Delphi contient une classe abstraite d'automate et une classe fille d'AEF Reconnaissant le langage aⁿb^p


Unit  UautomEF ;
 
 interface
 const 
   imposs =- 1 ; 
   fin = 20 ; 
   finmot = '#'; 
 type 
   T_etat = imposs..fin ; 
   Vt =char ; 
   T_transition =array [T_etat, char ]  of  T_etat ;
  
AutomateAbstr  =  class
 private
   Fmot :string ; 
   table : T_transition ;  {matrice des transitions} 
    procedure  setMot(s :string ) ;
   function  getMot :string ;
   function  transition(q : T_etat ; car : Vt) : T_etat ;
   procedure  Symsuiv (n : integer ; var  car : Vt) ;
 protected
   EtatFinal  :  T_etat ;
  procedure  init_table ;  virtual ;   abstract ;
 public
  property  Mot :string read  getmot  write  setMot ;
  procedure  Analyser ;
  constructor  Create(fin :integer ) ;
end;

AutomateEF = class (AutomateAbstr)
  protected
  procedure  init_table ; override;
end;

Implementation
{--- AutomateAbstr ---}
  constructor  AutomateAbstr.Create(fin :integer ) ;
 begin
  if  fin  in  [1..20]  then
    EtatFinal := fin
   else
    EtatFinal := 20 ;
   Fmot := '#';
   init_table ;
 end;
 
 function  AutomateAbstr.getMot : string ;
 begin
  result  :=  Fmot ;
 end;
 
 procedure  Symsuiv (n : integer ; var  car : Vt) ;
 begin
   car  :=  Fmot[n] ;
 end;
 
 procedure  AutomateAbstr.setMot(s : string ) ;
 var  long  : integer ;
 begin
   long := length(s) ;
  if  long <> 0  then
  begin
   if  s[long] <> '#' then
     Fmot := s + '#';
  end
  else
    Fmot  :=  '#';
 end;
 
 function  AutomateAbstr.transition(q : T_etat ; car : Vt) : T_etat ; 
  {par la table de transition :} 
  begin 
   q  :=  table[q,car] ; 
  result  :=  q ; 
 end;
 
 procedure  AutomateAbstr.Analyser ;
 var 
   etat  :  t_etat ;  
   numcar  : integer ;
   s  : string ;  
   symlu  :  vt ;
  begin
    numcar := 1 ; 
    etat := 0 ; 
   while  (etat <> imposs) and (etat <>  EtatFinal)  do 
   begin 
     Symsuiv (numcar , symlu) ; 
     numcar :=  numcar + 1 ;
     {fournit dans symlu le symbole suivant} 
     etat :=  self.transition(etat,symlu) ; 
   end;
   if  etat  = etatfinal  then
     writeln ( 'chaine reconnue !' )
    else
     writeln ( 'blocage, chaine non reconnue !' )
   end;
   {--- AutomateEF ---}
  procedure  AutomateEF.init_table ;
  {initialisation de la table des transitions} 
  var   i : t_etat ;  
   j : 0..255 ;  
   k :char ;
  begin
   for  i := imposs  to  fin  do 
    for  j := 0  to  255  do 
      table[i,chr(j)] := imposs ;
    {par défaut tout est non reconnu} 
    table[0, 'a' ] := 1 ; 
    table[1, 'a' ] := 1 ; 
    table[1, 'b' ] := 2 ; 
    table[2, 'b' ] := 2 ; 
    table[2,finmot] :=  EtatFinal ;
  end;
end.


Programme utilisant la classe AutomateEF et reconnaissant le langage L = { aⁿb^p / (n < 2) et (p < 2) }

program  ProjAutomEF ;    {$APPTYPE CONSOLE}   uses    SysUtils,   UAutomEF  in  'UAutomEF.pas';  var  AEFD : AutomateEF ;      begin     AEFD :=  AutomateEF.Create(3) ;     AEFD.Mot := 'aaaaabbbbb';     AEFD.Analyser ;     readln ;   end.

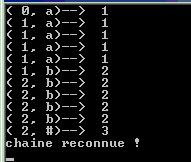
Exécution de ce programme sur l’exemple aaaaabbbbb : Exécution de ce programme sur l’exemple aaaaabbabb :

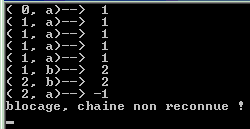
Nous remarquons dans ce dernier paragraphe, que nous avons mis en place un procédé général qui permet de construire méthodiquement en Delphi une classe d'AEFD, uniquement en changeant le contenu de la méthode init_table. Nous avons en fait mis au point un générateur manuel de programme Delphi pour AEFD.



Par la suite, nous utiliserons ce procédé à chaque fois que nous aurons à programmer un AEFD. Nous n’aurons seulement qu’à déclarer une nouvelle classe héritant de AutomateAbstr définie plus haut et implémenter par redéfinition sa méthode init_table : 

  AutomateEF  =  class  ( AutomateAbstr )
  protected
      procedure  init_table ; override;
end;

Implementation
  ( * ---  AutomateEF 
 Reconnaissant le langage L  =  { aⁿb^p / (n < 2) et (p < 2) }
  ---* )
  procedure  AutomateEF.init_table ;
  {initialisation de la table des transitions} 
  var   i : t_etat ;  
   j : 0..255 ;  
   k :char ;
  begin
   for  i := imposs  to  fin  do 
    for  j := 0  to  255  do 
      table[i,chr(j)] := imposs ;
    {par défaut tout est non reconnu} 
    table[0, 'a' ] := 1 ; 
    table[1, 'a' ] := 1 ; 
    table[1, 'b' ] := 2 ; 
    table[2, 'b' ] := 2 ; 
    table[2,finmot] :=  EtatFinal ;
  end;

( en pascal de base Pascal.Automates \aefnd.pas )

Le lecteur trouvera dans ce dossier le programme en pascal non objet "aefnd.pas " l’automate non déterministe A₁ (normalisé) vu précédemment dans ce chapitre.

Nous terminons ce chapitre en détaillant deux exercices de construction de programmes selon la méthode qui vient d’être décrite. Le lecteur pourra en inventer d’autres basés sur la même idée.
 

3.3 Exemple : les identificateurs pascal-like

 ( en pascal de base Pascal.Automates \Pasidentif.pas )

On donne des diagrammes syntaxiques de construction des identificateurs Pascal :

identificateur :


 



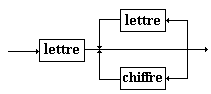
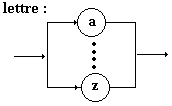
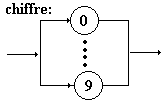
Construisons un programme Delphi reconnaissant de tels identificateurs, en utilisant le procédé de génération manuelle.

Méthode de travail adoptée

Détermination d’une grammaire G adéquate. Construction de l’automate AEFD associé à G. Programme pascal associé à l’automate construit.


 

Détermination d’une grammaire G_id adéquate

Nous remarquons d’abord qu’il y a une grammaire de type 3 engendrant ces identificateurs :

Soient les ensembles :
Lettre = { a, b,..., z }. // les 26 lettres de l’alphabet
Chiffre = { 0, 1,..., 9 }. // les 10 chiffres
V_T = Chiffre È Lettre È {#}.
V_N = { áidentificateurñ,A }

Posons G_id = (V_T , V_N , áidentificateurñ ,Règles ) une grammaire où
Axiome : áidentificateurñ
Règles :
áidentificateurñ¾®a |b|...|z A
A¾®a |b|...|z A
A¾®0 |1|...|9 A
A¾®#

G_id est de type 3 déterministe.
 

Construction de l’automate associé à G_id

Afin de réduire le nombre de lignes de texte, nous adoptons les conventions d’écriture suivantes :
 

( qk ,Lettre ) ¾® qi , représente l’ensemble des 26 règles : ( qk ,a ) ¾® qi ...... ( qk ,z ) ¾® qi

( qk , Chiffre) ¾® qi , représente l’ensemble des 10 règles : ( qk ,0 ) ¾® qi ...... ( qk ,9 ) ¾® qi

Etats associés aux éléments de V_N:
áidentificateurñ Û q₀
áAñ Û q₁
Etat initial = q₀
Etat final = q_f

Vocabulaire terminal de l’automate :
V_T^’ = V_T È {#} = Chiffre È Lettre È {#}

Règles de l’automate associé à G_id :
( q₀ , Lettre ) ¾® q₁// 26 règles
( q₁ , Lettre ) ¾® q₁// 26 règles
( q₁ , Chiffre ) ¾® q₁// 10 règles
( q₁ ,# ) ¾® q_f

Soit un total de 63 règles.

Graphe de l’automate :

 

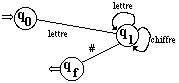
Matrice de transitions de l’automate: 

 
 
 

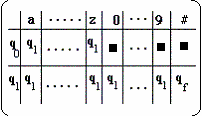
Programme Delphi associé à l’automate

Nous héritons de la classe AutomateAbstr.
Nous n’avons que la méthode init_table à redéfinir.

La partie déclaration est la même que celle que nous avons déjà fournie auparavant au paragraphe " fonction de transition à partir d’une matrice ".

AutomateEF  =  class  ( AutomateAbstr )
  protected
    procedure  init_table ; override;
end;

implementation
 
 procedure  AutomateEF.init_table ;
  {initialisation de la table des transitions} 
  var   i : t_etat ;  
   j : 0..255 ;  
   x :char ;
  begin
   for  i := imposs  to  fin  do 
    for  j := 0  to  255  do 
      table[i,chr(j)] := imposs ;
   for  x := 'a' to 'z' do 
   begin 
     table[0,x] := 1 ;   {  (q0,lettre) ¾® q1  } 
     table[1,x] := 1 ;   {  (q1,lettre) ¾® q1  } 
    end; 
   for  x := '0' to '9' do 
     table[1,x] := 1 ;   {  (q1,chiffre) ¾® q1  } 
    table[1,finmot] :=  EtatFinal ;   {  (q1,#) ¾® qf  } 
   end;
  

Programme utilisant la classe AutomateEF et reconnaissant le langage des identificateurs

program  ProjAutomEF ;    {$APPTYPE CONSOLE}   uses    SysUtils,   UAutomEF  in  'UAutomEF.pas';  var  AEFD : AutomateEF ;      begin     AEFD :=  AutomateEF.Create(3) ;     AEFD.Mot := 'v14bcd73';     AEFD.Analyser ;     readln ;   end.

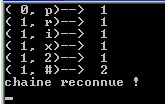
Exécution de ce programme sur l’exemple prix2 :   Exécution de ce programme sur l’exemple v14bcd73 :

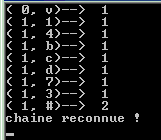
3.4 Exemple : les constantes numériques

 ( en pascal de base Pascal.Automates \ctdecim.pas )

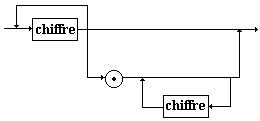
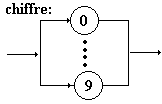
On donne des diagrammes syntaxiques de construction des constantes décimales positives Pascal-like :

constante :


 

Construisons un programme Delphi reconnaissant de telles constantes en utilisant le procédé de génération manuelle.
 

Méthode de travail adoptée :(identique à la précédente)

Détermination d’une grammaire G adéquate. Construction de l’automate AEFD associé à G. Programme pascal associé à l’automate construit.


 

Détermination d’une grammaire G_cte adéquate

Nous reconnaissons d’abord qu’il y a une grammaire de type 3 engendrant ces identificateurs :

Soient les ensembles :

EnsChiffre = { 0, 1,..., 9 }. // les 10 chiffres
V_T = EnsChiffre
V_N = { áconstanteñ,A,B }
Posons G_cte = (V_T , V_N , á constante ñ ,Règles ) une grammaire où
Axiome : á constante ñ
Règles :
á constante ñ¾®0 |1|...|9 A
A ¾®0 |1|...|9 A
A ¾®e
A ¾®. B
B ¾®0 |1|...|9 B
B ¾®e

G_cte est de type 3 déterministe.
 

Construction de l’automate associé à G_cte
Afin de réduire le nombre de lignes de texte, nous adoptons les mêmes conventions d’écriture suivantes que celles de l’exemple précédent:
 
 

( qk , Chiffre) ¾® qi , représente l’ensemble des 10 règles : ( qk ,0 ) ¾® qi ...... ( qk ,9 ) ¾® qi

Etats associés aux éléments de V_N:
á constante ñ Û q₀
áAñ Û q₁
áBñ Û q₂
Etat initial = q₀
Etat final = q_f

Vocabulaire terminal de l’automate :
V_T^’ = V_T È {#} = Chiffre È {#}

Règles de l’automate associé à G_cte :
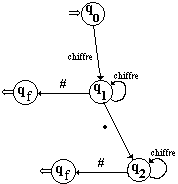
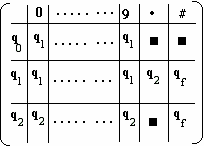
( q₀ , Chiffre) ¾® q₁// 10 règles
( q₁ , Chiffre ) ¾® q₁// 10 règles
( q₁ ,# ) ¾® q_f
( q₁ ,. ) ¾® q₂
( q₂ , Chiffre ) ¾® q₂// 10 règles
( q₂ ,# ) ¾® q_f

Soit un total de 33 règles.

Graphe de l’automate :


Matrice de transitions de l’automate:

Programme utilisant la classe AutomateEF et reconnaissant le langage des constantes numériques

program  ProjAutomEF ;    {$APPTYPE CONSOLE}   uses    SysUtils,   UAutomEF  in  'UAutomEF.pas';  var  AEFD : AutomateEF ;      begin     AEFD :=  AutomateEF.Create(3) ;     AEFD.Mot := 145.78;     AEFD.Analyser ;     readln ;   end.

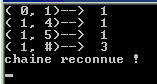
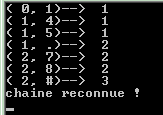
Exécution de ce programme sur l’exemple prix2 :   Exécution de ce programme sur l’exemple v14bcd73 :

Nous appliquons cette connaissance toute neuve à un petit projet de construction d’un interpréteur pour un langage analysable par grammaire de type 3. Nous verrons comment utiliser le graphe d’un automate dans le but de programmer les décisions d’interprétation. Là aussi, le lecteur pourra aisément adapter la méthodologie à d’autres exemples semblables construits sur des K-grammaires.