4.1.développement
méthodique
du Logiciel
Plan
du chapitre:
Introduction
1.
Production
du logiciel
1.1 Génie logiciel
1.2 Cycle de vie du logiciel
1.3 Maintenance d’un logiciel
1.4 Production industrielle
du logiciel
2.
Conception
structurée descendante
2.1 Critère simple
d’automatisation
2.2 Analyse méthodique
descendante
2.3 Analyse ascendante
2.4 Programmation descendante
avec
retour sur un niveau
2.5 Machines abstraites
et niveaux logiques
3.
Notion
d’ALGORITHME
3.1 Langage algorithmique
3.2 Objets de base d'un
langage algorithmique
3.3 Opérations sur
les objets de base d'un langage algorithmique
4.
Un
langage de description d’algorithme : LDFA
4.1 Atomes du LDFA
4.2 Information en LDFA
4.3 Vocabulaire terminal
du LDFA
4.4 Instructions simples
du LDFA
5.
Le
Dossier de développement
5.1 Enoncé et spécification
5.2 Méthodologie
5.3 Environnement
5.4 Algorithme en LDFA
5.5 Programme en langage Pascal
6.
Trace
formelle d’un algorithme
6.1 Espace d’exécution
d’une instruction composée
6.2 Exemple avec trace
formelle
7.
Traducteur
élémentaire LDFA - Pascal
7.1 Traducteur
7.2 Exemple
7.3 Sécurité
et ergonomie
8.
Facteurs
de qualité du logiciel
Introduction
Le bon sens est la chose du monde la mieux partagée...la
diversité de nos opinions ne vient pas de ce que les uns sont plus
raisonnables que les autres, mais seulement de ce que nous conduisons nos
pensées par diverses voies, et ne considérons pas les mêmes
choses. Car ce n'est pas assez d'avoir l'esprit bon, mais le principal
est de l'appliquer bien.
R Descartes Discours de la méthode, première
partie, 1637.
 PanneauProgAlgo.dif\PresProgAlgo.exe
PanneauProgAlgo.dif\PresProgAlgo.exe
Le développement méthodique
d’un logiciel passe actuellement par une démarche de " descente
concrète " de la connaissance que l’humain a sur la problématique
du sujet, vers l’action élémentaire exécutée
par un ordinateur. Le travail du programmeur étant alors ramené
à une traduction permanente des actions humaines en actions machines
(décrites avec des outils différents).
Nous pouvons en première
approximation différentier cette " descente concrète " en
un classement selon quatre niveaux d’abstraction :
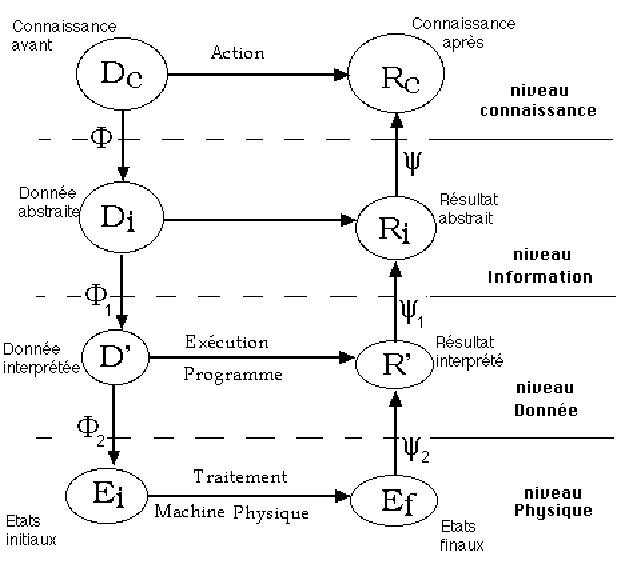 schéma
de descente concrète
schéma
de descente concrète
Nous voyons que toute activité
de programmation consiste à transformer un problème selon
une descente graduelle de l’humain vers la machine. Ici nous avons résumé
cette décomposition en 4 niveaux. La notion de programmation structurée
est une réponse à ce type de décomposition graduelle
d’un problème. L’algorithmique est la façon de décrire
cette méthode de travail.
1.
Production du logiciel
1.1 Génie logiciel
A une certaine époque, à
ses débuts, l’activité d’écriture du logiciel ne reposait
que sur l’efficacité personnelle du programmeur laissé pratiquement
seul devant la programmation d’un problème.
De nos jours, le programmeur
dispose d’outils et de méthodes lui permettant de concevoir et d’écrire
des logiciels. Le terme logiciel, ne désigne pas seulement
les programmes associés à telle application ou tel produit
: il désigne en plus la documentation nécessaire à
l'installation, à l'utilisation, au développement et à
la maintenance de ce logiciel. Pour de gros systèmes, le temps de
réalisation peut être aussi long que le temps du développement
des programmes eux-mêmes.
Le génie logiciel
concerne l'ensemble des méthodes et règles relatives à
la production rationnelle des logiciels. L'activité de développement
du logiciel, vu les coûts qu'elle implique, est devenue une activité
économique et doit donc être planifiée et soumise
à des normes sinon à des attitudes équivalentes à
celles que l'on a dans l'industrie pour n'importe quel produit. C'est pourquoi
dans ce cours, le mot-clef est le mot "composant logiciel" qui tient
à la fois de l'activité créatrice de l'humain et du
composant industriel incluant une activité disciplinée
et ordonnée basée pour certaines tâches sur des
outils formalisés.
D'autre part le génie
logiciel intervient lorsque le logiciel est trop grand pour que son développement
puisse être confié à un seul individu ; ce qui n'est
pas le cas pour des débutants, à qui il n'est pas confié
l'élaboration de gros logiciels. Toutefois, il est possible de sensibiliser
le lecteur débutant à l’habitude d’élaborer un logiciel
d’une manière systématique et rationnelle à l’aide
d’outils simples.
1.2 Cycle de vie du logiciel
Comme il faut un temps très
important pour développer un grand système logiciel, et que
d’autre part ce logiciel est prévu pour être utilisé
pendant longtemps, on sépare fictivement des étapes distinctes
dans ces périodes de développement et d’utilisation. Le modèle
dit de la cascade de Royce (1970) accepté par tout le monde informatique
est un bon outil pour le débutant. S’il est utilisé pour
de gros projets industriels, en supprimant les recettes et les validations
en fin de chaque phase, nous disposons en initiation d’un cadre méthodologique.
Il se présente alors sous forme de 8 diagrammes ou phases :
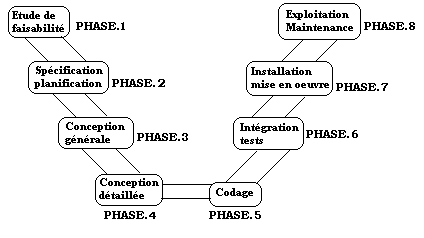
1.3 Maintenance d’un logiciel
Dans beaucoup de cas le coût
du logiciel correspond à la majeure partie du coût total d'une
application informatique. Dans ce coût du logiciel, la maintenance
a elle-même une part prépondérante puisqu'elle est
estimée de nos jours au minimum à 75% du coût total
du logiciel.
La maintenance est de trois sortes
:
-
adaptative (s’adapter à un
nouvel environnement...)
-
corrective (corrections d’erreurs...)
-
perfective (améliorations
demandées par le client...)
1.4 Production industrielle
du logiciel
La production du logiciel étant
devenue une activité industrielle et donc économique, elle
n’échappe pas aux données économiques classiques.
On répertorie un ensemble de caractéristiques associées
à un projet de développement, chaque caractéristique
se voyant attribuer un ratio de productivité.
Le
ratio de productivité d’une caractéristique
C’est le rapport entre la productivité
(exprimée en nombre d’Instructions Sources Livrées, par homme
et par mois) d’un projet exploitant au mieux cette caractéristique,
et la productivité d’un projet n’exploitant pas du tout cette caractéristique.
Le tableau suivant est tiré d’une étude de B.Boehm (Revue
TSI 1982 : les facteurs de coût du logiciel):

Tableau comparatif des divers
ratios de productivité (B.Boehm)
Vous aurez remarqué
en lisant le graphique précédent que le facteur le plus important
n'est pas l'expérience d'un langage (erreur commise par les néophytes).
Ce qui explique entre autres arguments que l'enseignement de la programmation
ne soit pas l'enseignement d'un langage. Il apparaît que le facteur
le plus coûteux reste un facteur sur lequel la technologie n'a aucune
prise : l'aptitude qu'ont des individus à communiquer entre eux
!
Pour l’élaboration d’un
logiciel, nous allons utiliser deux démarches classiques : la méthode
structurée ou algorithmique et plus tard une extension orientée
objet de cette démarche.
2.
Conception structurée descendante
2.1 Critère simple
d’automatisation
Un problème est
automatisable
(traitable par informatique) si :
-
l'on peut parfaitement définir
les données et les résultats,
-
l'on peut décomposer
le passage de ces données vers ces résultats en une suite
d'opérations élémentaires dont chacune peut être
exécutée par une machine.
|
Dans le cadre d’une initiation
à la programmation, dans le cycle de vie déjà présenté
plus haut, nous ne considérerons que les phases 2 à 6, en
supposant que la faisabilité est acquise, et qu’enfin les phases
de mise en oeuvre et de maintenance sont mises à part.
Dans cette perspective,
le
schéma de la programmation d’un problème se réduit
à 4 phases :
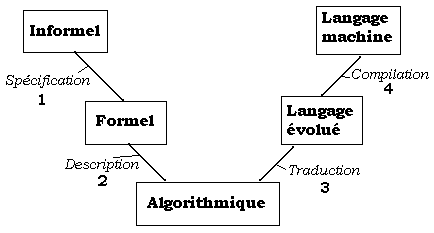
La phase 1 de spécification
utilisera les types abstraits de données (TAD), la phase 2 (correspondant
aux phases 3 et 4 du cycle de vie) utilisera la méthode de programmation
algorithmique, la phase 3 (correspondant à la phases 5 du cycle
de vie) utilisera un traducteur manuel pascal, la phase 4 (correspondant
à la phases 6 du cycle de vie) correspondra au passage sur la machine
avec vérification et jeux de tests.
Nous utiliserons un "
langage algorithmique " pour la description d’un algorithme résolvant
un problème. Il s’agit d’un outil textuel permettant de passer de
la conception humaine à la conception machine d’une manière
souple pour le programmeur.
Nous pouvons résumer
dans le tableau ci-dessous les étapes de travail et les outils conceptuels
à utiliser lors d’une telle démarche.
| ETAPES
PRATIQUES |
Matériel
et moyens techniques à disposition |
| Analyse |
Papier, Crayon, Intelligence,
Habitude. |
Mise en forme de
l’algorithme |
C’est l’aboutissement de l’analyse,
esprit logique et rationnel. |
| Description |
Utilisation pratique des outils
d’une méthode de programmation, ici la prog. structurée. |
| Traduction |
Transfert des écritures
algorithmiques en langage de programmation, ici en Pascal. |
| Tests et mise au point |
Mise au point du programme sur
des valeurs tests ou à partir de programmes spécialisés. |
| Exécution |
Phase finale : le programme s’exécute
sans erreur. |
2.2 Analyse
méthodique descendante
Le second [précept], de diviser chacune des
difficultés que j'examinerais, en autant de parcelles qu'il se pourrait
et qu'il serait requis pour les mieux résoudre.
R Descartes Discours de la méthode, seconde
partie, 1637.
Définir le
problème à résoudre:
expliciter
les données
préciser:
leur nature
leur domaine
de variation
leurs propriétés
expliciter
les résultats
préciser:
leur structure
leur relations
avec les données
fin définir;
Décomposer le
problème en sous-problèmes;
Pour chaque sous-problèmes
identifié faire
si solution
évidente alors écrire
le morceau de programme
sinon appliquer
la méthode au sous-problème
fsi
fpour. |
démarche proposée par J.Arsac
Cette démarche
méthodique a l'avantage de permettre d'isoler les erreurs lorsqu'on
en commet, et elles devraient être plus rares qu'en programmation
empirique (anciens organigrammes).
Il apparaît donc
plusieurs niveaux de décomposition du problème (niveaux d'abstraction
descendants). Ces niveaux permettent d'avoir une description de plus en
plus détaillée du problème et donc de se rapprocher
par raffinements successifs d'une description prête à la traduction
en instructions de l'ordinateur.
Afin de pouvoir décrire
la décomposition d'un problème à chaque niveau, nous
avons utilisé un langage algorithmique (et non pas un langage de
programmation) qui emprunte beaucoup au langage naturel (le français
pour nous).
2.3 Analyse ascendante
Le troisième [précept], de conduire par
ordre mes pensées, en commençant par les objets les plus
simples et les plus aisés à connaître, pour monter
peu à peu, comme par degrés, jusqu'à la connaissance
des plus composés; et supposant même de l'ordre entre ceux
qui ne se précèdent point naturellement les uns les autres.
R Descartes Discours de la méthode, seconde
partie, 1637.
Nous essaierons de partir de
l’existant (les fichiers sources déjà écrits sur le
même sujet) et de reconstruire par étapes la solution. Le
problème dans cette méthode est d’assurer une bonne cohérence
lorsque l’on rassemble les morceaux. Les méthodes objets que nous
aborderons plus loin, sont un bon exemple de cette démarche. Nous
n'en dirons pas plus dans ce paragraphe en renvoyant le lecteur intéressé
au chapitre de la programmation orientée objet de cours.
2.4
Programmation descendante avec retour sur un niveau
Comme partout ailleurs, une attitude
appuyée sur les deux démarches est le gage d’une certaine
souplesse dans le travail. Nous adopterons une démarche d’analyse
essentiellement descendante, avec la possibilité de remonter en
arrière dès que le développement paraît trop
complexe.
Nous adopterons dans tout le
reste du chapitre une telle méthode descendante (avec quelques retours
ascendants). Nous la dénommerons " programmation algorithmique ".
Nous utilisons les concepts de
B.Meyer
pour décomposer un problème en niveaux logiques puis en raffinant
successivement les différentes étapes.
2.5 Machines abstraites et
niveaux logiques
Principe
:
On décompose
chacune des étapes du travail en niveaux
d’abstractions logiques. On suppose en outre qu’à chaque niveau
logique fixé, il existe une machine abstraite virtuelle capable
de comprendre et d’exécuter la description du problème sous
la forme algorithmique en cours. Ainsi, en descendant de l’abstraction
vers le concret, on passe graduellement d’un énoncé de problème
au niveau humain à un énoncé
du même problème à un niveau où la machine
devient capable de l’exécuter.
| Niveau logique |
Machine abstraite |
Enoncé du
problème en |
0
|
M0
= l’humain |
A0
= langage naturel |
1
|
M1
= mach. Abstraite |
A1
= lang.algorithmique |
. . .
|
. . .
|
. . .
|
n
|
Mn
= machine+OS |
An
= langage évolué |
n+1
|
Mn+1=
machine physique |
An+1=
langage binaire |
A partir de cette
décomposition on construit un " arbre " de programmation représentant
graphiquement les hiérarchies des machines abstraites.
Voici un exemple
d’utilisation de cette démarche dans le cas de la résolution
générale de l’équation du second degré dans
R.
Le problème
se décompose en deux sous-problème " résolution d’une
équation du premier degré strict " ou problème " résolution
d’une équation du second degré strict " .
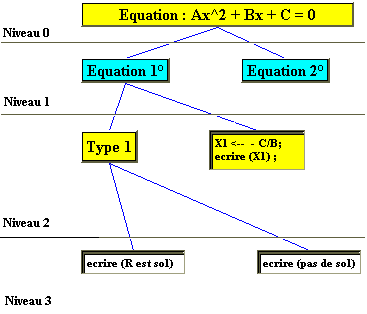
figure de la branche d’arbre 1er degré
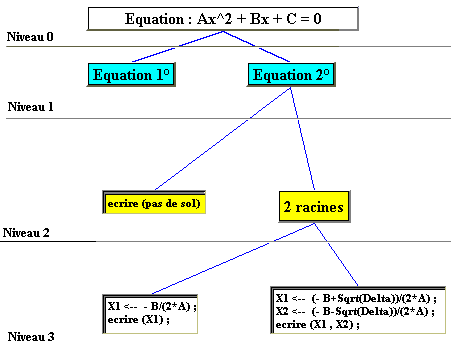
figure de la branche d’arbre 2ème degré
Nous avons utilisé
comme langage de description des étapes intermédiaires un
langage algorithmique basé sur le français. Nous le détaillerons
plus tard.
3.
Notion d’ALGORITHME
Définition
(D.E. Knuth)
Un algorithme est un ensemble
de règles qui décrivent une séquence d’opérations
en vue de résoudre un problème donné bien spécifié.
Un algorithme doit répondre aux 5 caractéristiques suivantes
:
-
La finitude
-
La précision
-
Le domaine des entrées
-
Le domaine des sorties
-
L’exécutabilité
|
Notons qu’un algorithme exprime
donc un procédé séquentiel (or dans la vie courante
tout n’est pas nécessairement séquentiel comme par exemple
écouter un enseignement et penser aux prochaines vacances), et ne
travaille que sur des problèmes déjà transformés
de la phase 1 à la phase 2 (la spécification). Il n’est pas
demandé aux débutants de travailler sur cette étape
du processus. C’est pourquoi la plupart des exercices de débutant
sont déjà spécifiés dans l’énoncé,
ou bien leur spécification est triviale.
-
Le nombre d’étapes d’un algorithme
doit être fini. Le temps d’exécution pourra être évalué.
-
Chaque étape doit être
parfaitement définie. Toutes les actions élémentaires
doivent être connues.
-
Le champ des données d’entrée
doit être spécifié.
-
Un algorithme ayant un résultat,
il faut donner les champs correspondants aux résultats de sortie,
ou du moins les relations entre les données d’entrée et les
données de sortie.
-
Un algorithme doit déboucher
sur un programme exécutable en un temps fini et raisonnable.
Environnement
On appelle environnement d’un
algorithme l’ensemble des entités utilisés par le processeur
pendant le déroulement de l’algorithme.
Nous allons définir un
langage de description des algorithmes qui nous permettra de décrire
les arbres de programmation et le fonctionnement des machines abstraites
de la programmation structurée.
3.1 Langage algorithmique
Voici classiquement ce que tous
les auteurs utilisent comme système de description d’un algorithme
lorsqu’ils le font avec un langage. Les paragraphes 1 et 2 indiquent les
éléments fondamentaux d’un tel langage, le paragraphe 3 en
construit un. Nous
verrons que l’algorithmique est par nature plus proche de l’étudiant
que la machine. En effet dans la suite du cours, l’étudiant s’apercevra
que les nombres rationnels ne sont pas représentables simplement
en machine, encore moins les nombres réels. Le langage d’implémentation
étudié (Pascal) étant relativement pauvre à
cet égard.
L’étudiant ne doit pas
croire que l’informatique s’est résignée à ne travailler
que sur les entiers et les décimaux, mais plutôt se rendre
compte qu’il existe une palette importante de certains produits informatiques
qui traitent plus ou moins efficacement les insuffisances des langages
classiques par exemple vis à vis des rationnels (les systèmes
de calcul formel comme MAPLE (étudié en Taupe),MATHEMATICA,...
sont une réponse à ce genre d’insuffisance).
Nous ne nous préoccupons
absolument pas, dans un premier temps en algorithmique, ni de la vérification,
ni du contrôle, ni des restrictions d’implantation des données.
Notre préoccupation première est d’écrire des algorithmes
justes qui fonctionnent sur des données justes.
3.2 Objets de base d'un
langage algorithmique
Contenant
| Nous appelons contenant
toute cellule mémoire d’une machine abstraite d’un niveau fixé. |
Contenu
| Nous appelons contenu
l’information représentée par l’état du contenant. |
Atomes
| Pour un contenant fixé
on note A l’ensemble de tous ses états possibles, on dit aussi ensemble
des atomes du niveau n (niveau du contenant). |
Remarques
:
a) un atome de niveau n est donc un état possible d’un contenant,
b) pour un niveau logique fixé, il y a un nombre d’atomes fini,
c) lorsque l’on est au niveau machine :
-
le contenant est à p positions binaires( p est le nombre de bits
du mot, p>1).
-
A ={0,1}x....x {0,1} , p fois
|
Adresse fictive
| Toute machine abstraite de niveau
fixé dispose d’autant de cellules mémoires que nécessaire.
Elles sont repérées par une adresse fictive (à
laquelle nous n’avons pas accès). |
Nom
| Par définition, à
toute adresse nous faisons correspondre bijectivement par l’opération
nom,
un identificateur unique définissant pour l’utilisateur la cellule
mémoire repérée par cette adresse : |
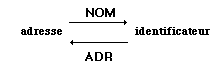
Nous
définissons aussi un certain nombre de fonctions :
Etat : Adresse¾®Atome
(donne
l’état associé à une adresse)
valeur: identificateur¾®Atome
(donne
l’état associé à un
identificateur,
on dit la valeur)
contenu: Atome¾®information(donne
le contenu informationnel
de
l’atome)
signification:
identificateur ¾®information(sémantique
de
l’identificateur) |
Les
fonctions précédentes sont liées par le schéma
suivant :
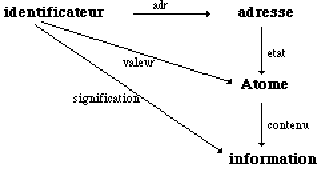
3.3 Opérations sur
les objets de base d'un langage algorithmique
Les parenthèses d’énoncé
en LDFA seront algol-like, nous disposerons d’un debut et
d’une
fin .
Exécutant ou
processeur algorithmique
| Nous appelons exécutant
ou processeur, la partie de la machine abstraite capable de lire,
réaliser, exécuter des opérations sur les atomes de
cette machine, ceci à travers un langage approprié. |
Remarque:
l’opérateur formel exécutant dépend du temps.
Instruction simple
| C’est une instruction exécutable
en un temps fini par un processeur et elle n’est pas décomposable
en sous-tâches exécutables ou en autres instructions simples.
Ceci est valable à un niveau fixé. |
Instruction composée
| C’est une instruction simple,
ou bien elle est décomposable en une suite d’instructions entre
parenthèses. |
Composition séquentielle
| Si i,j,...,t représentent
des instructions simples ou composées, nous écrirons la composition
séquentielle avec des " ; ". La suite d’instructions " i ; j; ......
; t " est appelée une suite d’instructions séquentielles. |
Schéma fonctionnel
C’est :
-
soit un identificateur,
-
soit un atome,
-
soit une application :
(identificateur)p¾®
identificateur
(où p>0)
|
Espace d’exécution
L’espace d’exécution
d’une instruction, c’est le n-uplet des n identificateurs ayant au moins
une occurrence dans l’instruction (ceci à un niveau fixé).
Soit une instruction ik,
l’ensemble Ek des variables, ayant au moins une occurrence dans
l’instruction ik est noté : Ek={x1,x2,.....,xp} |
Environnement
| C’est l’ensemble des objets
et des structures nécessaires à l’exécution d’un travail
donné pour un processeur fixé (niveau information). |
Action
| C’est l’opération ou
le traitement déclenché par un événement qui
modifie l’environnement (ou bien toute modification de l’environnement); |
Action primitive
| Pour un processeur donné(d’une
machine abstraite d’un niveau fixé)une action est dite primitive,
si l’énoncé de cette action est à lui seul suffisant
pour que le processeur puisse l’exécuter sans autre éléments
supplémentaires. Une action primitive est décrite par une
instruction
simple du processeur. |
Action complexe
| Pour un processeur donné(d’une
machine abstraite d’un niveau fixé)une action complexe est une action
non-primitive,
qui est décomposable en actions primitives (à la fin
de la phase de conception elle pourra être exprimée soit par
un module de traitement, soit par une instruction composée). |
Remarques
:
-
Ce qui est action primitive pour
une machine abstraite de niveau n, peut devenir une action complexe pour
une machine abstraite de niveau n+1, qui est l’expression de la précédente
à un plus bas niveau (d’abstraction).
-
Les instructions du langage doivent
être les mêmes pour tous les niveaux de machine abstraite,
sinon la programmation devient trop lourde à gérer.
-
Tout langage de description de machine
abstraite n’est pas implantable sur ordinateur (en tout cas partiellement
sinon ce serait un langage de programmation). Il ne peut servir qu’à
décrire en partie la spécification et la conception. De plus
il doit utiliser les idées de la programmation structurée
descendante modulaire.
|
4.
Un langage de description d’algorithme : LDFA
AVERTISSEMENT
| L'apprentissage d'un langage
de programmation ne sert qu'aux phases 3 et 4 (traduction et exécution)
et ne doit pas être confondu avec l'utilisation d'un langage algorithmique
qui prépare le travail et n'est utilisé que comme plan de
travail pour la phase de traduction. En utilisant la construction d'une
maison comme analogie, il suffit de bien comprendre qu'avant de construire
la maison, le chef de chantier a besoin du plan d'architecte de cette maison
pour passer à la phase d'assemblage des matériaux ; il en
est de même en programmation. |
Voici l’énoncé
d’un langage simple, extensible, qui sera utilisé dans tout le reste
du document et qui va servir à décrire les algorithmes. Nous
le dénoterons par la suite LDFA pour
Langage
de Description Formel d’Algorithme (terminologie non
standard utilisée par l'auteur pour dénommer rapidement un
langage algorithmique précis).
4.1 Atomes du LDFA
-
Les ensembles de nombres comme N,Z,Q,R
(les vrais ensembles classiques des mathématiques et leurs structures
connues).
-
La grammaire mathématique
et celle du français.
-
{V,F} comme éléments
logiques (({V,F},Ø
, Ù ,
Ú
) étant une algèbre de Boole)
-
Les prédicats.
-
Les caractères du français
et les chaînes de caractères C
des machines.
4.2 Information en LDFA
On rappelle qu’une information
en LDFA est obtenue par le contenu d’un atome et se construit à
l’aide de:
-
la grammaire du français
et le sens commun des mots,
-
les théorèmes et les
résultats obtenus des théories mathématiques(le sens
étant le sens habituel donné à tous les symboles),
-
toutes les manipulations générales
(algorithmes en particulier) sur les structures de données.
4.3 Vocabulaire terminal
du LDFA
VT = {¬
, W , lire()
, ecrire( ) , si , tantque , alors , ftant
, faire , fsi , sinon ,sortirSi, pour
,repeter , fpour , jusque , ; , entrée
,sortie , Algorithme , local , global , principal
, modules , specifications , types-abstraits , debut
, fin , ( , ) , [ , ] , * , + , - , / , Ø
,
Ù
, Ú }
4.4
INSTRUCTIONS SIMPLES DU LDFA :
 Lancer
l'API associé
Lancer
l'API associé
4.4.1 Instruction vide
| syntaxe : W |
| sémantique
: ne rien faire pendant
un temps de base du processeur. |
4.4.2 Affectation
syntaxe : a ¬a
où : aÎ
identif,
et a est
un schéma fonctionnel. |
sémantique
:
1) si
a
=identificateur
alors val(a)=val(a)
2) si a
est
un atome alors val(a)=a
3) si a
est
une application : a
:
(id1,.....,idp)¾®
a(id1,.....,idp)
alors val(a)=a’(val(id1),.....,val(idp))
où a’
est
l’interprétation de a dans
l’ensemble des valeurs des val(idk) |
4.4.3 Lecture
Elle permet d’attribuer une valeur
à un objet en allant lire sur un périphérique d’entrée
et elle range cette valeur dans l’objet.
| syntaxe : lire(a)
(où a Î
identif) |
| sémantique
: le contexte de la
phrase précise où l’on lit pour "remplir" a, sinon on indique
lire(a)
dans
..... |
4.4.4 Ecriture
Ordonne au processeur d’écrire
sur un périphérique (Ecran, Imprimante, Port, Fichier etc...)
| syntaxe : ecrire(a)
(où a Î
identif) |
| sémantique
: le contexte de la
phrase précise où l’on écrit pour "voir" a, sinon
on indique ecrire(a) dans ..... |
4.4.5 Condition
syntaxe : si
P alors E1 sinon E2 fsi
où P est un prédicat
ou proposition fonctionnelle,
E1 et E2 sont deux instructions
composées. |
sémantique : classique
de l’instruction conditionnelle,
si le processeur n’est pas lié
au temps on peut écrire :
si P alors
E1 sinon W
fsi º
si P
alors
E1 fsi
Nous notons º
la
relation d’équivalence entre instructions. Il s’agit d’une équivalence
sémantique, ce qui signifie que les deux instructions donnent les
mêmes résultats sur le même environnement. |
4.4.6 Boucle tantque
syntaxe : tantque
P faire E ftant
où P est un prédicat
et E une instruction composée) |
sémantique :
tantque P faire
E ftant º
siP
alors
(E ; tantque P faire E ftant) fsi |
Remarques
:
au sujet de la relation
"º"
qui
est la notation pour l’équivalence sémantique en LDFA, on
considère un "programme" LDFA non pas comme une suite d’instructions,
mais comme un environnement donné avec un état initial E0
, puis on évalue la modification de cet environnement que chaque
action provoque sur lui:
{E0} ¾®
{E1}¾®
{E2}
¾®
...........¾® {Ek}¾®
{Ek+1}
où action n+1 : {En}¾®
{En+1}.
On obtient ainsi une suite d’informations sur l’environnement :(E0,E1,....Ek+1) |
Nous dirons alors que deux instructions
(simples ou composées) sont sémantiquement équivalentes
(notation º
)si leurs actions associées sur le même environnement de départ
provoquent la même modification. A chaque instruction est associée
une action sur l’environnement, c’est le résultat qui est le même
(même état de l’environnement avant et après) :
Soient : Instr1 ¾®
action1 (action associée à Instr1),
Instr2 ¾®
action2 (action associée à Instr2),
E et E’ deux états de
l’environnement,
si nous avons : {E} action1
{E’} et {E} action2 {E’},alors Instr1 et Instr2 sont sémantiquement
équivalentes, nous le noterons :
Instr1 ºInstr2
4.4.7 Boucle répéter
syntaxe : repeter
E jusqua P
(où P est un prédicat
et E une instruction composée) |
sémantique :
repeter E jusqua
P º E
; tantque ¬P
faire
E
ftant |
Exemple d’équivalence
entre itérations:
| tantque
P faire E ftant º
si
P alors (repeter E jusqua ¬P)
fsi
repeter E jusqua
P º E
; tantque ¬P
faire
E
ftant
(par
définition) |
4.4.8 Boucle pour
syntaxe : pour
x ¬
a jusqua b faire E fpour
(où E est une instruction
composée, x une variable, a et b des expressions dans un ensemble
fini F totalement ordonné, la relation d’ordre étant notée
£
, le successeur d’un élément x dans l’ensemble est noté
Succ(x) et son prédécesseur pred(x)) |
sémantiques
:
Cette boucle fonctionne
à la fois en suivant automatiquement l’ordre croissant dans l’ensemble
fini F ou en suivant automatiquement l’ordre décroissant, cela dépendra
de la position respective de départ de la borne a et de la borne
b. La variable x est appelée un indice de boucle.
sémantique
dans le cas ordre croissant à partir du tantque :
x ¬a
;
tantque x
£
succ(b)faire
E ;
x ¬succ(x)
;
ftant
sémantique
dans le cas ordre décroissant à partir du tantque :
x ¬
a ;
tantque x ³
pred(b) faire
E ;
x ¬
pred(x) ;
ftant |
Exemple simple :
-
E = N(entiers
naturels)et la relation d’ordre : £
= inférieur ou égal dans N
-
pour i ¬
x jusquà y faire R FinPour
(ici i prendra toutes les valeurs
successives dans N comprises
entre x et y soient, x+y-1 valeurs et s’incrémentera de 1 à
chaque fois)
4.4.9 Sortie de boucle
| syntaxe : SortirSi
P (où P est un prédicat)ne peut être utilisée
qu’à l’intérieur d’une itération (tantque,répéter,pour). |
| sémantique
: termine par anticipation
et immédiatement l’exécution de la boucle dans laquelle l’instruction
SortirSi
se trouve. |
4.4.10 Exemple récapitulatif
Reprenons l’exemple précédent
de l’équation du second degré en décrivant dans l’arbre
de programmation l’action de la machine abstraite de chaque niveau à
l’aide d’instructions LDFA :
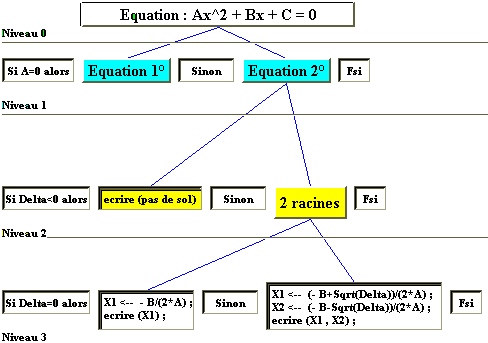
figure de la branche d’arbre
2ème degré
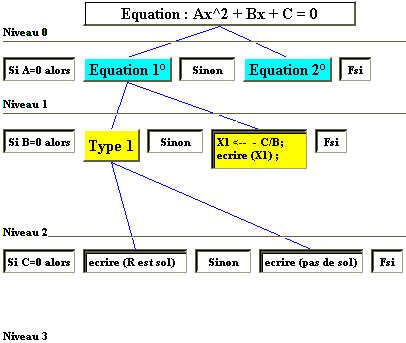
figure de la branche d’arbre
1er degré
En relisant cet arbre
selon un parcours en préordre (
il s’agit de parcourir l’arbre en partant de la racine et descendant toujours
par le fils le plus à gauche, puis ensuite de passer au fils droit
suivant etc…), l'on obtient après avoir complété
l’algorithme une écriture linéaire comme suit :
Algorithme Equation
Entrée:
A,B,C
Î
R3
Sortie:
X1
,X2
Î
R2
Local:
D
Î R
début
lire(A,B,C);
Si
A=0 alors {A=0}
début
Si
B = 0 alors
Si
C = 0 alors
écrire(R
est solution)
Sinon
{C¹0}
écrire(pas
de solution)
Fsi |
Sinon
{B¹0}
début
X1
¬
-C/B;
écrire (X1)
fin |
Fsi |
fin
Sinon
{A¹0}
début
D ¬
B² -4*A*C ;
Si
D
< 0 alors
écrire(pas de solution)
Sinon{
D ³0}
Si
D
= 0 alors
début
X1
¬
-B/(2*A);
écrire(X1)
fin |
Sinon{
D > 0}
début
X1
¬
(-B+sqrt(D))/(2*A);
X2
¬
(-B-sqrt(D))/(2*A);
écrire( X1
,
X2
)
fin |
Fsi |
Fsi |
fin
Fsi
FinEquation
Nous regroupons toutes les informations
de conception dans un document que nous appelons le dossier de programmation.
Des algorithmes complets exécutables
pas à pas dans l'assistant "exemples d'algorithmes  ".
".
5.
Le Dossier de développement
C’est un document dans lequel
se trouvent consignés tous les éléments relatifs à
la construction et à l’écriture de l’algorithme et du programme
résolvant le problème cherché. Nous le divisons en
5 parties.
5.1 Enoncé et spécification
Enoncé du problème
résolu par ce logiciel.
-
Spécifications opérationnelles
des abstractions de plus haut niveau du logiciel, en exprimant celles-ci
à l'aide de types abstraits et de spécifications de plus
bas niveau.
-
Spécifications des types
abstraits de données utilisés.
-
Spécifications d'interface
pour les abstractions de plus bas niveau.
On utilisera ces trois techniques
de spécification de manière descendante, quitte à
remonter corriger des spécifications de niveau plus haut lorsque
des erreurs seront apparues dans une spécification de plus bas niveau.
Ces spécifications sont destinées au niveau " concepteur
de logiciel ", plutôt qu'à l'utilisateur. Cette partie rassemble
les définitions abstraites des composants. Un utilisateur de base
n'ayant à priori pas à consulter ce paragraphe, les termes
employés seront les plus rigoureux possibles relativement à
un formalisme éventuel.
Analyse
des besoins :
son utilité principale
est de fournir à l'utilisateur la description des services que lui
rendra ce logiciel. Les termes utilisés doivent être compris
par l'utilisateur.
5.2 Méthodologie
Dans ce paragraphe se situent
tous les documents et les explications qui ont pu mener à la décision
de résoudre le problème posé par la méthode
que l'on a choisie. Le programmeur dispose ici de toute latitude pour s'exprimer
à l'aide de texte en langue naturelle, de représentation
graphique, d'outils ou de supports permettant au lecteur de se faire une
idée précise du pourquoi des choix effectués.
5.3 Environnement
L’étudiant pourra présenter
sous forme d’un tableau les principales informations concernant les données
de son algorithme.
Exemple :
| Nom |
genre |
localisation |
utilisation |
| PHT |
reel |
Entrée |
prix hors taxe |
| TVA |
reel |
local |
TVA en % |
| PTTC |
reel |
sortie |
Prix TTC |
5.4 Algorithme en LDFA
Ici se situe la description
de l'algorithme proposé pour résoudre le problème
proposé. Il est obtenu entre autre à partir de l’arbre de
programmation construit pendant l’analyse et la conception.
Algorithme XYZT;
global :
local :
entrée :
sortie :
modules utilisés :
Spécifications
: (TAD)
Types Abstraits de Données utilisés
début
( corps d'algorithme en LDFA)
fin XYZT.
Nous verrons ailleurs ce que
représentent les notions de TAD et
de module.
5.5 Programme en langage
Pascal
Dans ce paragraphe nous ferons
figurer la " traduction " en Pascal de l’algorithme du paragraphe précédent
(la traduction est possible das beaucoup d'autres
langages).
6.
Trace formelle d’un algorithme
Et le dernier [précept], de faire partout des
dénombrements si entiers, et des revues si générales,
que je fusse assuré de ne rien omettre.
R Descartes Discours de la méthode, seconde
partie, 1637.
Nous proposons au débutant
de vérifier l'exactitude de certaines parties de son algorithme
en utilisant un petit outil permettant l'exécution formelle (c'est
à dire sur des valeurs algébriques ou symboliques plutôt
que numériques) de son algorithme. La trace numérique et
les vérifications associées seront effectuées lors
de l'exécution par la machine.
6.1 Espace d’exécution
d’une instruction composée
On appelle espace d’exécution
d’une séquence ou d’un bloc d’instructions i1...in
l’ensemble 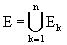 où
Ek est l’espace d’exécution de l’instruction ik.
où
Ek est l’espace d’exécution de l’instruction ik.
Rappelons que l’on peut considérer
un " programme " LDFA sous un autre point de vue : non pas comme une suite
d’instructions, mais comme un environnement donné avec un état
initial E0 , puis on évalue la modification de cet environnement
que chaque instruction provoque sur lui. On considère les instructions
ik comme des transformateurs d’environnement :
{E0} ¾®
{E1}¾®
{E2}
¾®
...........¾® {Ek}¾®
{Ek+1}
où in+1 : {En}¾®
{En+1}
Ces actions déterminent
alors une suite d’états de l’environnement (E0,E1,....Ek+1) que
l’on peut observer.
C’est ce point de vue qui permet
d’exécuter un suivi d’exécution symbolique d’un algorithme.
Nous le nommerons " trace formelle ".
On adoptera pour une trace formelle
une disposition en tableau de l’espace d’exécution comme suit :
| Etats |
V1 |
V2 |
..... |
Vn |
| E1 |
-- |
-- |
|
y |
| E2 |
x |
-- |
|
y+1 |
La colonne Etats représente
donc les états successifs de l’environnement (ou espace d’exécution)
figuré ici par les variables V1,V2,...,Vn. Les contenus des cellules
du tableau sont les valeurs symboliques des variables au cours du déroulement
de l’exécution.
6.2 Exemple avec trace formelle
Enoncé
Calculer S=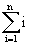 sans utiliser de formule (on sait que S=(n+1)n/2)
sans utiliser de formule (on sait que S=(n+1)n/2)
Spécification :
flux d’information
En Entrée
Un nombre
n Î
N*
En Sortie
Ecrire la
somme voulue S.
Méthodologie
Suite récurrente 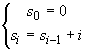
Environnement
| Nom |
genre |
localisation |
utilisation |
| N |
Entier |
Entrée |
Nombre d’éléments
à saisir |
| S |
Entier |
Sortie |
Variable de cumul pour la somme |
| i |
Entier |
local |
Gestion des boucles : compteur |
Algorithme
Algorithme Somentier
N
Î N*
S,I Î
N2
Début Algo
{initialisations};
(E0)
Lire(N) ;
(E1)
S ¬
0;
(E2)
I ¬
1;
(E3)
TantQue I £?
? ? faire
(E4)
S ¬
S+I;
(E5)
I ¬
I+1;
(E6)
FinTQ;
(E7)
Ecrire(S);
Fin Somentier
Ceci est un algorithme dans lequel
on a déjà intercalé les états (En)
entre les instructions. On ne sait pas exactement quel sera le test d’arrêt
de la boucle (remplacé par ? ? ?), on sait seulement que c’est la
valeur de i qui le fournira.
Utilisation
de la trace formelle
Nous allons montrer à
l’aide de la trace formelle que cet algorithme fournit bien la somme des
n premiers entiers dans la variable S, relativement aux préconditions
{ S = 0 et i = 1}. Nous allons donc faire de la démonstration de
programme : {S= 0 et i= 1} Algorithme {S = 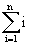 }
}
Tout d’abord nous supposerons
que le test n’est jamais franchi, c’est à dire que l’on a I > N.
Exécutons manuellement et pas à pas l’algorithme précédent,
voici le début des résultats de sa trace formelle dans le
tableau ci-dessous :
| Etats |
I |
N |
S |
| E0 |
- |
- |
-- |
| E1 |
- |
n |
-- |
| E2 |
- |
n |
0 |
| E3 |
1 |
n |
0 |
| E4=E3 |
1 |
n |
0 |
| E5 |
1 |
n |
1 |
| E6 |
2 |
n |
1 |
| E4=E6 |
2 |
n |
1 |
| E5 |
2 |
n |
3 |
| E6 |
3 |
n |
3 |
| E4 = E6 etc.. |
3 |
n |
3 |
isolons les deux premiers " tours
" de boucle :
| E4 = E6 |
2 |
n |
1 |
| E4 = E6.. |
3 |
n |
3 |
Nous voyons que juste avant la
sortie de boucle (état E6) au premier tour i=2 et S=1, au deuxième
tour i=3 et S=3 .
nous posons l’hypothèse
de récurrence qu’au kème tour i=k+1 et S=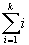 (somme
des k premiers entiers). Nous allons utiliser l’exécution formelle
pas à pas d’un tour de boucle afin de voir si après un tour
de plus cette hypothèse se vérifie au rang k+1 :
(somme
des k premiers entiers). Nous allons utiliser l’exécution formelle
pas à pas d’un tour de boucle afin de voir si après un tour
de plus cette hypothèse se vérifie au rang k+1 :
| Etats |
I |
N |
S |
| ..... |
... |
... |
... |
| E4=E6 |
k+1 |
n |
S=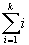 |
| E5 |
k+1 |
n |
S=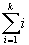 + k+1
+ k+1 |
| E6 |
k+2 |
n |
S=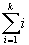 + k+1
+ k+1 |
Or S=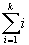 +k+1 =
+k+1 = 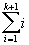 (la
somme des k+1 premiers entiers).
(la
somme des k+1 premiers entiers).
Nous venons donc de montrer
qu’à l’état E6 cet algorithme donne :
| Etats |
I |
N |
S |
| E6 |
k+1 |
n |
S=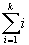 |
lorsque k=n nous avons dans S la
somme des n premiers entiers 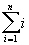 :
:
"
n, n>0, S=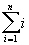
| Etats |
I |
N |
S |
| E6 |
n+1 |
n |
S=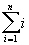 |
En plus ce tableau nous permet
immédiatement de trouver la valeur exacte de la variable de contrôle
de la boucle (ici la variable i qui vaut n+1) et donc d’écrire un
test d’arrêt de boucle juste.
On peut alors choisir comme test
I<>n+1 ou bien I< n+1 etc... ou tout autre prédicat équivalent.
Il était possible de programmer
directement cet algorithme avec les deux autres boucles (pour... et répeter...).
Ceci est proposé en exercice au lecteur.
7.
Traducteur élémentaire LDFA - Pascal
Nous venons de voir qu’un algorithme
devait se traduire en langage de programmation (dit évolué).
Nous fournirons ici un tableau qui sera utile à l’étudiant
pour la traduction des instructions algorithmiques en Pascal simple.
7.1 Traducteur
Voici le tableau de traduction
LDFA en Pascal simplifié relativement aux instructions seulement:
(P est un prédicat et
E une instruction composée)
| LDFA |
Pascal |
| W (instruction
vide) |
pas de traduction |
| debut i1 ; i2;
i3; ...... ; ik fin |
begin i1
; i2; i3; ...... ; ik end |
| x ¬
a |
x := a |
| ; |
(ordre d'exécution)
; |
| Si P alors
E1 sinon E2 Fsi |
if P then
E1 else E2
( attention défaut,
pas de fermeture !) |
| Tantque P faire
E Ftant |
while P do
E
( attention, pas de fermeture) |
| répeter
E jusquà P |
repeat E until
P |
| lire (x1,x2,x3......,xn
) |
read(fichier,x1,x2,x3......,xn
)
readln(x1,x2,x3......,xn )
Get(fichier) |
| ecrire (x1,x2,x3......,xn
) |
write(fichier,x1,x2,x3......,xn
)
writeln(x1,x2,x3......,xn )
Put(fichier) |
| pour x<-a
jusquà
b faire E Fpour |
for x:=a to
b do E (croissant)
for x:=a downto
b do E (décroissant)
( attention, pas de fermeture) |
| SortirSi
P |
if P then Break |
|
|
| N
(entiers naturels) |
integer |
| Z
(entiers relatifs) |
integer |
| Q
(rationnels) |
real |
| R
(réels) |
real |
| { Vrai,Faux }
(logique) |
boolean |
| caractère |
char |
| + , - , / , * |
+ , - , / , * |
| > , < , = , ¹ |
> , < , = ,<> |
| ³
, £ |
>= , <= |
| Ø,
Ù
, Ú |
not , and , or |
Ce tableau de traduction permet
déjà d’écrire très rapidement des programmes
Pascal simples à partir d’algorithmes étudiés et écrits
auparavant.
7.2 Exemple
En appliquant le traducteur à
l’algorithme de l’équation du second degré nous obtenons
le programme Pascal suivant :
program equation;
var
A,B,C:real;
X1,X2:real;
Delta:real;
begin
readln(A,B,C);
if A = 0 then{A=0}
if B = 0 then
if C = 0
then
writeln('R est solution')
else
writeln('pas de solution') |
else {B¹0}
begin
X1 := - C/B;
writeln('x=',X1)
end |
|
else {A¹0}
begin
Delta := B*B-4*A*C;
if Delta < 0 then
writeln('pas de solution')
else {
D³0}
if Delta=0 then
begin
X1 := -B/(2*A);
writeln('x=',X1)
end |
else {
D > 0}
begin
X1 := (-B + Sqrt(Delta))
/ (2*A);
X2 := (-B - Sqrt(Delta))
/ (2*A);
writeln('x1=',X1,'x2=',X2)
end |
|
|
end
end.
7.3 Sécurité
et ergonomie
L’utilisation du traducteur manuel
LDFA à
Pascal fournit une version préliminaire de programme pascal fonctionnant
sur des données correctes sans aucune présentation. Il appartient
au programmeur de compléter dans un deuxième temps la partie
sécurité associée aux contraintes du domaine de définition
des variables et aux contraintes matérielles d’implantation. Enfin,
dans un troisième temps, l’ergonomie (forme de l’échange
d’information entre le programme et le futur utilisateur) sera envisagée
et programmée. Voyons sur l’exemple de la somme des n premiers entiers
déjà cité plus haut, comment ces trois étapes
s’articulent .
Etape de traduction
Voici le texte final de l’algorithme
de départ :
Algorithme Somentier
N
Î N*
S,I ÎN2
Début
Lire(N) ;
S ¬
0;
I ¬
1;
TantQue I <
N+1 faire
S ¬
S +I;
I ¬
I+1;
FinTQ;
Ecrire(S);
Fin Somentier
Voici le texte de sa traduction
en pascal :
program Somentier
;
var N :
integer ;
S,I
: integer ;
begin
readln(N) ;
S :=0 ;
I :=1 ;
while I
< N+1
do begin
S := S +I;
I := I+1;
end;
writeln(S)
end.
Etape de sécurisation
Sécurité
due aux domaines de définition des données
La traduction ne permet pas d’écrire
les domaines de définition des variables : en l’occurrence ici la
variable N Î N*
est
traduite par " var N :integer ", or le type prédéfini
integer
est un sous-ensemble de Z, il est donc nécessaire d’éliminer
les entiers négatifs ou nuls comme choix possible. Dès que
l’utilisateur aura entré son nombre, le programme devra tester l’appartenance
au bon intervalle afin de protéger la partie de code (signalée
en dessous dans le cadre).
| program Somentier
; |
program Somentier
; |
| var N : integer
;
S,I : integer ; |
var N : integer
;
S,I : integer ; |
| begin
readln(N) ;
|
begin
readln(N) ;
if N
> 0 then begin |
| S :=0 ;
I :=1 ; |
S :=0 ;
I :=1 ; |
| while I < N+1
dobegin
S := S + I; |
while I < N+1
do
begin
S := S + I; |
| I := I+1;
end;
writeln(S)
|
I := I+1;
end;
writeln(S)
end |
| end. |
end. |
Sécurité
due aux contraintes d’implantation
Si nous exécutons ce programme
pour la valeur N=500, la valeur fournie en sortie est " -5822 " sur un
pascal 16 bits comme TP-pascal. Nous sommes confrontés au problème
de la représentation des entiers machines déjà cité.
Ici le type integer est restreint à l’intervalle [-32768,+32767]
;
il y a manifestement dépassement de capacité (overflow) et
le système a allègrement continué les calculs malgré
ce dépassement. En effet, la somme vaut 500*501/2 soit 125250 qui
n’est pas dans l’intervalle des integer.
Le programmeur doit donc remédier
à ce problème par un effort personnel de sécurisation
de son programme en n’autorisant les calculs que pour des valeurs valides
offrant un maximum de sécurité.
Ici la variable S contient la
somme 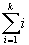 ,
nous savons que
,
nous savons que 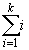 = k(k+1)/2, donc il suffira de résoudre dans N l’inéquation k(k+1)/2 £
32767 où n est l’inconnue. L’unique solution positive a pour partie
entière 255. En vérifiant sur l’exécution, nous trouvons
que S = 32640 pour N = 255. Ce qui nous donne la version suivante du programme
:
= k(k+1)/2, donc il suffira de résoudre dans N l’inéquation k(k+1)/2 £
32767 où n est l’inconnue. L’unique solution positive a pour partie
entière 255. En vérifiant sur l’exécution, nous trouvons
que S = 32640 pour N = 255. Ce qui nous donne la version suivante du programme
:
| program
Somentier ; |
var
N : integer ;
S,I : integer ; |
begin
readln(N) ;
if (N > 0) and
(N < 256) then begin |
S :=0 ;
I :=1 ; |
while
I< N+1 do begin
S := S +I; |
I := I+1;
end;
writeln(S)
end |
| end. |
Etape d’ergonomie
Dans cet exemple, l’information
à échanger avec l’utilisateur est très simple et ne
nécessite pas une interface spéciale. Il s’agira de lui préciser
les contraintes d’entrée et de lui présenter d’une manière
claire le résultat.
| program
Somentier ; |
var
N: integer ;
S, I : integer ; |
begin
Write(‘Entrez un entier entre 0 et
255’) ;
readln(N) ;
if (N > 0) and (N
< 256) then begin |
S :=0 ;
I :=1 ; |
while
I< N+1 do begin
S := S +I; |
I := I+1;
end;
writeln(‘la somme des ‘,N,’ premiers entiers
vaut ‘,S)
end
else writeln(‘Calcul impossible
! !’) |
| end. |
Vous remarquerez que les adjonctions
supplémentaires de code (en italique) dans le programme final
se montent à environ 50% du total du code écrit, car un logiciel
n’est pas uniquement un algorithme traduit. En continuant d’appliquer le
principe de la programmation structurée, il est bon de bien séparer
lors du développement la partie algorithmique des parties sécurité
et ergonomie. Le programmeur débutant y gagnera en clarté
dans sa méthode de travail.
8.
Facteurs de qualité du logiciel
B.Meyer et G.Booch
constat :
| Un utilisateur, lorsqu’il achète un produit comme un appareil
électro- ménager ou une voiture, attend de son acquisition
qu’elle possède un certain nombre de qualités (fiabilité,
durabilité,efficacité,...). Il en est de même avec
un logiciel. |
Voici une liste minimale de critères de qualité
du logiciel (d’après B.Meyer, G.Booch):
Reprenons les définitions
communément admises par ces deux auteurs sur ces facteurs de qualité.
| La
correction
est la qualité qu'un logiciel a de respecter les spécifications
qui ont été posées. |
| La
robustesse
est la qualité qu'un logiciel a de fonctionner en se protégeant
des conditions de dysfonctionnement. |
| L'extensibilité
est la qualité qu'un logiciel a d’accepter des modifications dans
les spécifications et des adjonctions nouvelles. |
| La
réutilisabilité
est la qualité qu'un logiciel a de pouvoir être intégré
totalement ou partiellement sans réécriture dans un nouveau
code. |
| La
compatibilité
est la qualité qu'un logiciel a de pouvoir être utilisé
avec d'autres logiciels sans autre effort de conversion des données
par exemple. |
| L'efficacité
est la qualité qu'un logiciel a de bien utiliser les ressources. |
| La
portabilité
est la qualité qu'un logiciel a d'être facilement transféré
sur de nombreux matériels, et insérable dans des environnements
logiciels différents. |
| La
vérificabilité
est la qualité qu'un logiciel a de se plier à la détection
des fautes, au traçage pendant les phases de validation et de test. |
| L'intégrité
est la qualité qu'un logiciel a de protéger son code et ses
données contre des accès non prévus. |
| La facilité
d'utilisation est la qualité qu'un logiciel a de pouvoir être
appris, utilisé, interfacé, de voir ses résultats
rapidement compris, de pouvoir récupérer des erreurs courantes. |
| La
lisibilité
est la qualité qu'un logiciel a d'être lu par un être
humain. |
| La
modularité
est la qualité qu'un logiciel a d'être décomposable
en éléments indépendants les uns des autres et répondants
à un certain nombre de critères et de principes. |
| L'abstraction
est la qualité qu'un logiciel a de s’attacher à décrire
les opérations sur les données et à ne manipuler ces
données qu’à travers ces opérations. |
La production de logiciels de
qualité n’est pas une spécificité des professionnels
de la programmation ; c’est un état d’esprit induit par les méthodes
du génie logiciel. Le débutant peut, et nous le verrons par
la suite, construire des logiciels ayant des " qualités " sans avoir
à fournir d’efforts supplémentaires. Bien au contraire la
réalité a montré que les étudiants " bricoleurs
" passaient finalement plus de temps à " bidouiller " un programme
que lorsqu’ils décidaient d’user de méthode de travail. Une
amélioration de la qualité générale du logiciel
en est toujours le résultat.
![]() PanneauProgAlgo.dif\PresProgAlgo.exe
PanneauProgAlgo.dif\PresProgAlgo.exe
 schéma
de descente concrète
schéma
de descente concrète








