Objectif : développer un exemple simple de construction d'une machine abstraite par décomposition descendante sur 4 niveaux.
 

ENONCE

On se donne une liste de n noms (composés de lettres uniquement). Extrayez ceux qui sont le premier et le dernier par ordre alphabétique. Ecrire un programme Pascal effectuant cette opération.
 

SPECIFICATIONS :(il s'agit d'éclaircir certaines décisions)

Plan:
a) Objets utilisés,
b) machine abstraite,
c) spécification de données.
 
 

Objets utilisés au niveau 0 :

1° (Liste, << ): où Liste est un ensemble fini de noms
où << est une relation d'ordre total

2° Noms :ensemble de tous les noms possibles (chacun est constitué de lettres)

3° élément : N* x Liste ® Liste, (fonction fournissant le kième élément de la liste)

(k,Liste) ® élément(k,Liste)Î Liste

4° Grand ÎNoms, Petit ÎNoms

5° Long : Liste ® N*, (fonction fournissant le nombre d’éléments de la liste)
 

Grand ¬élément ( 1 , Liste) ;
Petit ¬ élément ( 1 , Liste) ;
Pour indice ¬ 2 jusquà Long(Liste) faire
Si Grand << élément(indice,Liste)alors

{Grand = le dernier et Petit = le premier }

Nous avons ici une spécification abstraite de haut niveau. Il est impératif de prendre des décisions sur les structures de données qui vont être utilisées. Nous allons envisager le cas le plus simple : celui où la structure choisie pour représenter la liste est un tableau.
 

Reprise des objets abstraits en les exprimant de la façon suivante :

Nous continuons à descendre dans les niveaux d’abstraction. Nous devons prendre des décisions sur le langage-cible. Il est dit dans l'énoncé que ce doit être Pascal, mais lequel ?

Nous allons choisir là aussi une version simple en prenant par exemple comme dialecte deux descendants de l'UCSD-Pascal, à savoir Think Pascal (Mac) ou Borland Pascal (PC) qui contiennent en prédéfini le type de chaîne de caractères.
 

Machine abstraite de niveau 2 - cas A:

Algorithme Principal EXTRAIT0
Global : n Î N* , Long_mot Î N*
Local : indice Î N*, ( Grand , Petit ) Î Noms2
Spécification:

Cet algorithme se traduit immédiatement en pascal. Nous voyons donc qu’il nous a été possible d’écrire ce petit programme en descendant uniquement sur 2 niveaux de spécifications.

Qu’en est-il lorsque l’on travaille avec un autre langage cible (nous allons juste utiliser une version différente du même langage cible) ? Nous allons voir que nous devrons descendre alors plus loin dans les spécifications et développer plus de code c'est l'objectif de la suite de ce document.
 

Machine abstraite CMP de niveau 2’ - cas B:

Reprenons partiellement la même spécification de données par un tableau de taille n pour la Liste, mais supposons que le langage-cible soit du Pascal ISO, dans lequel le type string n’existe pas.

Nous allons alors définir un nom comme étant lui-même une liste de caractères.

Nous voyons que se pose alors la même question que pour l'objet Liste. Nous choisirons, afin de ne pas nous perdre en complexités inutiles, de spécifier la liste de caractères par un tableau de caractères : notons le Tchar.

Ce choix de spécification induit un choix de développement d'une machine abstraite spécifique à la relation d'ordre, qui n'est pas un opérateur simple du langage : notons la machine CMP.

Noms = Tchar
Taille de Tchar = n
ch1 Î Tchar , ch2 Î Tchar
 

Spcéfications fonctionnelles de niveau 2’- cas B :

Spécification de l’opérateur ‘ << ’de comparaison de chaînes :

<< : Tchar x Tchar  ® { Vrai , Faux }

<<(ch1,ch2) = Vrai   ssi   (ch1 < ch2) ou (ch1 = ch2)

<<(ch1,ch2) = Faux   ssi   ch2 < ch1
 
 

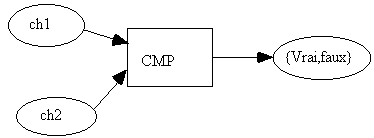- ch1 Î Noms, - ch2 Î Noms

Spécifions les données Nom et Liste de la machine abstraite CMP:
 

Un nom :   1     2                 Long_mot

Noms = Tableau de caractères   Attributs :  Taille = Long_mot caractère spécial = #

 

Une liste de noms :

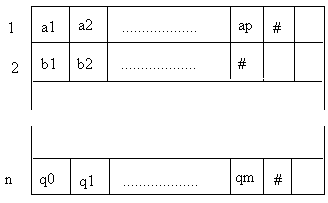
Liste = Tableau de noms       Attribut :    Taille = n

Machine abstraite CMP de niveau 3’ - cas B :

Décrivons une première version de CMP en tenant compte des spécifications de données précédentes.
 

Tantque (les caractères lus de ch1 et de ch2 sont les mêmes)
et
(ch1 non entièrement exploré)
et
(ch2 non entièrement exploré) faire
  passer au caractère lu suivant dans ch1 ;
  passer au caractère lu suivant dans ch2 ;
Ftant ;
Si (ch1 et ch2 finis en même temps) alors ch1=ch2 fsi ;
Si (ch1 fini avant ch2) ou (car_Lu de ch1 < car_Lu de ch2) alors

Descendons plus bas dans les niveaux d’abstraction.
 

Notre travail va consister à expliciter, à l'aide des structures de données choisies les phrases de haut niveau d'abstraction de la spécification de niveau 3’ de CMP (en italique le niveau 3’, en gras le niveau 4’):

car_Lu de ch1 = ch1[i] (ième caractère de ch1)
car_Lu de ch2 = ch2[k] (kème caractère de ch2)
ch1 fini ou entièrement exploré = { ch1[i]=# }
ch2 fini ou entièrement exploré = { ch2[k]=# }
les caractères de ch1 et de ch2 sont les mêmes = { ch1[i]=ch2[i] }
caractère suivant de chi[k] = chi[k+1] (où 1 <= i <= 2)

La spécification opérationnelle de niveau 4’ de CMP devient alors :

Tantque (ch1[k] = ch2[k] ) et ( ch1[k] ¹ # ) et ( ch2[k] ¹ # ) faire
    k ¬ k+1
Ftant ;
Si ( ch1[k] = # ) et ( ch2[k] = # ) alors CMP ¬ Vrai fsi ;
Si ( ch1[k] = # ) ou (ch1[k] < ch2[k] ) alors CMP ¬ Vrai fsi ;
Si ( ch2[k] = # ) ou (ch2[k] < ch1[k] ) alors CMP ¬ Faux fsi ;

Il faut prévoir d'initialiser le processus au premier caractère k=1 d'où maintenant une spécification de l'algorithme :
 

Algorithme CMP
Local : k Î N*
entrée :( ch1 , ch2 ) Î Noms2
sortie : CMP Î{Vrai,Faux}
Spécification:

Puis en intégrant la machine abstraite CMP de niveau 4’ dans la spécification de l'algorithme choisi en b) avec les spécifications de TAD décrites précédemment nous obtenons l'algorithme principal suivant :

Algorithme Principal EXTRAIT1
Global : n  Î N* , Long_mot Î N*
Local : indice Î N*, ( Grand , Petit ) Î Noms2
module utilisé : CMP.
Spécification:

• Tableau de caractère de dimension 1.
• Tableau de Noms de dimension 1.

La version d’implantation de CMP du niveau 4’ a été conçue sur une structure de données tableau terminée par une sentinelle (le caractère #). Elle a été implantée par une fonction en pascal.

Il est possible de réécrire d’autres version d’implantation de cette même machine CMP avec des structures de données différentes comme un tableau avec un attribut de longueur ou bien une structure liste dynamique. Nous engageons le lecteur à écrire à chaque fois l’algorithme associé et à le traduire en un programme pascal.

Nous donnons au lecteur les trois versions d’implantation en pascal de la fonction CMP associée.
 
Nous engageons le lecteur à écrire à chaque fois l’algorithme associé et à le traduire en un programme pascal. 

CMP avec sentinelle :

function CMP(ch1,ch2:Nom):Boolean;
var
 k : integer;
begin
 k:=1
 While (ch1[k]=ch2[k])and(ch1[k]<>'#')and(ch2[k]<>'#') do k:=k+1;
 if (ch1[k]='#')and(ch2[k]='#') then CMP:=True;
 if (ch1[k]='#')or(ch1[k]<ch2[k]) then CMP:=True;
 if (ch2[k]='#')or(ch2[k]<ch1[k]) then CMP:=False;
end;{CMP}
 

CMP avec pointeur :

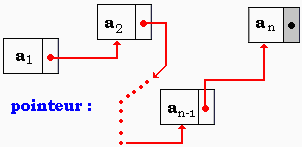
type pchaine=^chaine;
 chaine=record
   car:char;
   suiv:pchaine;
 end;

function CMP(ch1,ch2:Nom):Boolean;
begin
 while ((ch1^.car=ch2^.car) and (ch1^.suiv<>nil)
  and (ch2^.suiv<>nil)) do
 begin
  ch1:=ch1^.suiv;
  ch2:=ch2^.suiv;
 end;
 if ((ch1^.suiv=nil) and (ch2^.suiv=nil)) then CMP:=true;
 if (((ch1^.suiv=nil) and (ch2^.suiv<>nil))
  or (ch1^.car<ch2^.car)) then CMP:=true;
 if (((ch2^.suiv=nil) and (ch1^.suiv<>nil))
  or (ch1^.car>ch2^.car)) then CMP:=false;
end;{CMP}
 

CMP avec attribut :

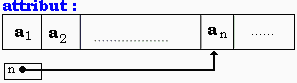
const MaxCar=1000;
type inter=0..MaxCar;
chaine=record
  long:integer;
  car:array[1..MaxCar] of char;
end;

function CMP(ch1,ch2:Nom):Boolean;
var n:integer;
begin
 n:=1;
 while (ch1.car[n]=ch2.car[n]) and ((n<>n1)
  and (n<>n2)) do n:=n+1;
 if ((n=ch1.long) and (n=ch2.long)) then CMP:=true;
 if(((n=ch1.long) and (n<>ch2.long))
  or (ch1.car[n]<ch2.car[n])) then CMP:=true;
 if((n=ch2.long) and (n<>ch1.long))
  or (ch1.car[n]>ch2.car[n]) then CMP:=false;
end;{CMP}