L'idée de considérer
les types de données comme une abstraction date des années
80. On s'est en effet aperçu qu'il était nécessaire de
s'abstraire de la représentation ainsi que pour l'abstraction fonctionnelle.
On a vu apparaître depuis une vingtaine d’année un domaine de
recherche : celui des spécifications algébriques. Cette
recherche a donné naissance au concept de Type Abstrait Algébriques
(TAA).
Selon ce point de vue
une structure de donnée devient:
| Une collection d’informations
structurées et reliées entre elles selon un graphe relationnel
établi grâce aux opérations effectuées sur ces
données. |
Nous spécifions d’une façon
simple ces structures de données selon deux niveaux d’abstraction,
du plus abstrait au plus concret.
Une spécification
abstraite :
Une spécification
opérationnelle :
| Description d’une forme d’implantation informatique choisie
pour représenter et décrire la structure de donnée.
Nous la divisons en deux étapes : la spécification opérationnelle
concrète (choix d’une structure informatique classique) et la spécification
opérationnelle d’implantation (choix de la description dans le langage
de programmation). |
Remarque
:
| Pour une spécification
abstraite fixée nous pouvons définir plusieurs spécifications
opérationnelles différentes. |
1. La notion de TAD (Type Abstrait de Données)
Bien que nous situant au niveau
débutant il nous est possible d’utiliser sans effort théorique
et mental compliqué, une méthode de spécification semi-formalisée
des données. Le " type abstrait de donnée " basé sur
le type abstrait algébrique est une telle méthode.
Le lecteur ne souhaitant pas
aborder le formalisme mathématique peut sans encombre pour la suite,
sauter le paragraphe qui suit et ne retenir que
le point de vue pratique de la syntaxe d’un TAA.
1.1 Le Type Abstrait Algébrique
(TAA)
Dans ce paragraphe nous donnons quelques
indications théoriques sur le support formel algébrique de
la notion de TAA.
Notion d’algèbre
formelle informatique
(notations de F.H.Raymond cf.Biblio)
Soit (Fn) n ÎN , une famille d’ensembles tels que :
| ($i0 ÎN (1 £i0 £ n) / Fi0 ¹ Æ) Ù("i,"j, i¹ j Þ Fi Ç Fj =
Æ) |
posons : I=
{ n ÎN / Fn ¹ Æ }
Vocabulaire
:
Les symboles ou éléments
de F0 sont appelés symboles de constantes ou symboles fonctionnels
0-aire,
les symboles de Fn
(où n ³ 1 et n ÎI) sont appelés
symboles fonctionnels n-aires. |
Notation
:
soit F* l’ensemble des expressions
sur F, le couple (F*,F) est appelé une algèbre
abstraite.
On définit pour tout symbole
fonctionnel n-aire 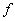 , une application de F*n dans F* notée "
, une application de F*n dans F* notée "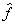 " de la façon suivante :
" de la façon suivante :
" e, (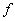 Î Fn ¾®
Î Fn ¾® 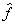 )
)
et {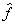 : F*n ¾® F*telle que (a1,...,an)¾®
: F*n ¾® F*telle que (a1,...,an)¾® 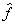 (a1,...,an)=
(a1,...,an)=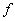 (a1,...,an) }
(a1,...,an) }
On dénote :
Fn ={ 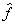 /
/ 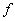 Î Fn }et
Î Fn }et 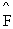 =ÈFn
=ÈFn
n ÎI |
le couple (F*,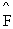 ) est appelé une algèbre formelle informatique (AFI).
) est appelé une algèbre formelle informatique (AFI).
Les expressions deF*construites à partir des
fonctions 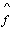 sur des symboles fonctionnels n-airess’appellent
des schémas fonctionnels.
sur des symboles fonctionnels n-airess’appellent
des schémas fonctionnels.
Par définition, les schémas
fonctionnels de F0 sont appelés les
constantes.
Exemple :
F0 =
{a,b,c} // les constantes
F1 = {h,k}
// les symboles unaires
F2 = {g} //
les symboles binaires
F3 = {f} //
les symboles ternaires
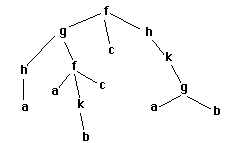
Soit le schéma fonctionnel
: fghafakbcchkgab
(chemin aborescent abstrait non parenthésé)
Ce schéma peut aussi s’écrire
avec un parenthésage :
f[g(h(a),f(a,k(b),c)),c,h(k(g(a,b)))]
ou encore avec une représentation
arborescente:
Interprétation
d’une algèbre formelle informatique
(notations de F.H.Raymond cf.Biblio)
Soit une algèbre formelle
informatique (AFI) : (F*,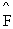 )
)
- on se donne un ensemble X
tel que X ¹ Æ ,
- X est muni d’un ensemble d’opérations sur
X notéW,
- l’on construit une fonction
y telle que :
y : (F*,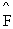 ) ¾® X ayant
les propriétés d’un homomorphisme
) ¾® X ayant
les propriétés d’un homomorphisme
y est appelée fonction d’interprétation
de l’AFI.
X est appelée l’univers de l’AFI.
Une AFI est alors un modèle
abstrait pour toute une famille d'éléments fonctionnels, il
suffit de changer le modèle d'interprétation pour implanter
une struture de données spécifique.
Exemple :
F0 = {x,y} une AFI
F2 = {f,g}
F = F0 È F2
l’Univers : X = R (les nombres réels)
les opérateurs W = {+,*} (addition et multiplication)
l’interprétation y : (F*,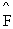 )¾® (R , W )
)¾® (R , W )
définie comme suit :
y(f) : R² ¾® R
y(f) : (a,b)¾® y( f
) [a,b] = a+b
y(g) : R² ¾® R
y(g) : (a,b) ¾® y( g ) [a,b] = a*b
y(x) = a0 (avec a0 ÎR fixé interprétant
la constante x)
y(y) = a1 (avec a1ÎR fixé interprétant la constante y)
Soit le schéma fonctionnel
fxgyx, son interprétation dans ce cas est la suivante :
y(fxgyx) = y(f(x,g(y,x))) = y(f)(y(x),y(g)[y(y),y(x)])
= y(x) + y(g)[y(y),y(x)]Ü propriété de y(f)
= y(x) + y(y)*y(x) Ü propriété dey(g)
Ce
qui donne comme résultat : y(fxgyx) = a0 + a1 * a0
A partir de la même AFI,
il est possible de définir une autre fonction d’interprétation
y’et un autre Univers
X’.
par exemple :
N (les entiers naturels)
et
W = { reste ,³}
(le reste de la division
euclidienne et la relation d’ordre)
La fonction y’est définie comme suit :
y’(g) :
N²¾® N
y’(g) :
(a,b)¾® y’(g)[a,b] = reste(a,b)
y’(f) :
N²¾® N
y’(f) : (a,b)¾® y’(f)[a,b] = a ³ b y’(x) = n0 (avec n0 ÎN fixé)
y’(y) = n1 (avec n1 Î N fixé)
On interprète alors le
même schéma fonctionnel dans ce nouveau cas fxgyx :
y’(fxgyx)
= n0 ³ reste(n1, n0)
Ceci n’est qu’une interprétation.
cette interprétation reste encore une abstraction de plus bas niveau,
le sens (sémantique d’exécution), s’il y en a un, sera donné
lors de l’implantation de ces éléments. Nous allons définir
un outil informatique se servant de ces notions d'AFI et d'interprétation,
il s'agit du type abstrait algébrique.
Un TAA (type abstrait algébrique)
est alors la donnée du triplet :
- une AFI
- un univers X et W
- une fonction d’interprétation
y
la syntaxe du TAA est
définie par l’AFI et l’ensemble X
la sémantique du TAA est
définie par y et l’ensemble W
Notre objectif étant
de rester pratique, nous arrêterons ici la description théorique
des TAA (compléments cités dans la bibliographie pour le lecteur
intéressé).
1.2 Disposition pratique
d'un TAA
on écrira (exemple fictif):
Sorte
: A, B, C ..... les noms de types définis
par le TAA, ce sont les types au sens des langages de programmation.
Opérations :
f : A x
B ¾® B
g : A ¾® C
x : ¾® B (notation pour les symboles de constantes de F0)
y : ¾® B (notation pour les symboles de constantes de F0)
Cette partie qui décrit
la syntaxe du TAA s’appelle aussi la
signature du TAA .
La sémantique est donnée
par (y , W )sous la forme d’axiomes et de préconditions.
Le domaine d’une opération
définie partiellement est défini par une précondition.
Un TAA réutilise des
TAA déjà définis, sous forme de hiérarchie.
Dans ce cas, la signature totale est la réunion des signatures de tous
les TAA.
Si des opérateurs utilisent
le même symbole, le problème de surcharge peut être
résolu sans difficulté, parce que les opérateurs sont
définis par leur ensembles de définitions.
SYNTAXE DE L’ECRITURE D’UN
TYPE ABSTRAIT ALGEBRIQUE :
| sorte : ...............
utilise
: ...........
opérations
:
préconditions
:
........ def_ssi
.......
axiomes
:
FinTAA
|
Exemple d’écriture
d’un TAA (les booléens) :
| sorte
: Booléens
opérations :
V
: ¾® Booléens
F : ¾® Booléens
¬ : Booléens ¾®
Booléens
Ù : Booléens x
Booléens ¾® Booléens
Ú : Booléens x
Booléens ¾® Booléens
axiomes :
¬(V) = F ; ¬(F) = V
a Ù V = a ; a Ù F = F
a Ú V = V ; a Ú F = a
FinBooléens
|
1.3 Le Type Abstrait de Donnée
(TAD)
 PanneauTAD.dif
PanneauTAD.dif
Dans la suite du document les
TAA ne seront pas utilisés entièrement, la partie axiomes étant
occultée. Seules les parties opérations et préconditions
sont étudiées en vue de leur implantation.
C’est cette restriction d’un TAA
que nous appellerons un type abstrait de données (TAD). Nous allons
fournir dans les paragraphes suivants quelques Types Abstrait de Données
différents.
Nous écrirons ainsi par
la suite un TAD selon la syntaxe suivante :
TAD Truc
utilise : ...........
Champs : ...........
opérations
: ...........
préconditions
: ...........
FinTAD Truc
Le TAD Booléens s’écrit à
partir du TAA Booléens :
|
TAD Booléens
opérations
:
V : ¾® Booléens
F :
¾® Booléens
¬ : Booléens ¾®
Booléens
Ù : Booléens x
Booléens ¾® Booléens
Ú : Booléens x
Booléens ¾® Booléens
FinTAD Booléen
|
Nous remarquons que cet outil
permet de spécifier des structures de données d’une manière
générale sans avoir la nécessité d’en connaître
l’implantation, ce qui est une caractéristique de la notion d’abstraction.
1.4 Classification hiérarchique
Nous situons, dans notre approche
pédagogique de la notion d’abstraction, les TAD au sommet de la hiérarchie
informationnelle :
HIERARCHIE INFORMATIONNELLE
- 1° TYPES ABSTRAITS
(les TAA,...)
- 2° CLASSES / OBJETS
- 3° MODULES
- 4° FAMILLES de
PROCEDURES et FONCTIONS
- 5° ROUTINES (procédures
ou fonctions)
- 6° INSTRUCTIONS
STRUCTUREES ou COMPOSEES
- 7° INSTRUCTIONS
SIMPLES (langage évolué)
- 8° MACRO-ASSEMBLEUR
- 9° ASSEMBLEUR
(langage symbolique)
- 10° INSTRUCTIONS
MACHINE (binaire)
Nous allons étudier dans la
suite 3 exemples complets de TAD classiques : la liste linéaire,
la pile LIFO1, la file
FIFO2. Pour chacun de
ces exemples, il sera fourni une spécification opérationnelle
en pascal, puis plus loin en Delphi.
| Exemples de types abstraits de données |
1.5 Le TAD liste linéaire
(spécifications abstraite et concrète)
 LearnP.dif
LearnP.dif
Spécification
abstraite
Répertorions les fonctionnalités d’une liste en
soulignant les verbes d'actions et les noms, à partir d’une description
semi-formalisée:
C’est une structure
de donnée séquentielle dans laquelle les données peuvent
être traitées les unes à la suite des autres.
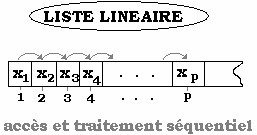
Il est possible
dans une telle structure d’ajouter ou de retirer des éléments
en n’importe quel point de la liste.
L’ordre des
éléments est primordial. Cet ordre est construit, non sur la
valeur des éléments de la liste, mais sur les places (rangs)de
ces éléments dans la liste.
Le modèle
mathématique choisi est la suite finie d’éléments
de type T0 :
(ai)iÎI où I est fini, totalement ordonné, ai
Î T0
Chaque place a un contenu
de type T0.
Le nombre d’éléments
d’une liste l est
appelé longueur de la liste. Si la liste est vide nous dirons
que sa longueur est nulle (longueur = 0 ).
On doit pouvoir effectuer
au minimum (non exhaustif) les actions suivantes sur les éléments
d’une liste l
: accéder à un élément de place fixée,
supprimer un élément de place fixée, insérer
un nouvel élément à une place fixée, etc ....
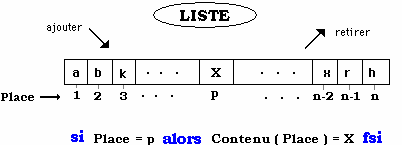
De cette description nous extrayons
une spécification sous forme de TAD.
Ecriture syntaxique du
TAD liste linéaire
TAD Liste
utilise : N,
T0, Place
Champs : (a1,.....,an)
suite finie dans T0
opérations
:
liste_vide : ¾® Liste
acces : Liste x N ¾® Place
contenu : Place ¾® T0
kème : Liste x N ¾® T0
long : Liste ¾® N
supprimer : Liste x N
¾® Liste
inserer : Liste x N x ¾® Liste
succ : Place ¾® Place
préconditions
:
acces(L,k) def_ssi
1 £ k £ long(L)
supprimer(L,k) def_ssi
1 £ k £ long(L)
inserer(L,k,e) def_ssi
1 £ k £ long(L)+1
kème(L,k) def_ssi
1 £ k £ long(L)
Fin-Liste
signification des
opérations :
(spécification
abstraite)
acces(L,k) : opération
générale d’accès à la position d’un élément
de rang k de la liste L.
supprimer(L,k) : suppression
de l’élément de rang k de la liste L.
inserer(L,k,e) : insérer
l’élément e de T0 , à la place de l’élément
de rang k dans la liste L.
kième(L,k)
: fournit l’élément de rang k de la liste.
spécification opérationnelle
concrète
- La liste est représentée
en mémoire par un tableau et un attribut de longueur.
- Le kème élément
de la liste est le kème élément du tableau.
- Le tableau est plus grand
que la liste (il y a donc dans cette interprétation une contrainte
sur la longueur. Notons Longmax cette valeur maximale de longueur de liste).
Il faut donc, afin de conserver
la cohérence, ajouter deux préconditions au TAD Liste
:
long(L) def_ssi
long(L) £ Longmax
inserer(L,k,e) def_ssi
(1 £ k
£ long(L)+1)
Ù (long(L) £ Longmax)
D’autre part la structure
de tableau choisie permet un traitement itératif de l’opération
kème ( une autre spécification récursive de cet opérateur
est possible dans une autre spécification opérationnelle de
type dynamique).
kème(L,k) =
contenu(acces(L,k) )
1.6 Le TAD pile LIFO (spécification
abstraite et concrète)
Spécification
abstraite
Répertorions
les fonctionnalités d’une pile LIFO (Last In First Out) en soulignant les verbes d'actions et les noms, à partir d’une description semi-formalisée:
- C’est un modèle
pour toute structure de donnée où l’on accumule des informations
les unes après les autres, mais où l’on choisit de n’effectuer
un traitement que sur le dernier élément entré. Exemples
: pile de dossiers sur un bureau, pile d’assiettes, etc...
- Il est possible dans
une telle structure d’ajouter ou de retirer des éléments
uniquement au début de la pile.
- L’ordre des
éléments est imposé par la pile. Cet ordre est construit
non sur la valeur des éléments de la liste, mais sur les places
(rangs)de ces éléments dans la liste. Cet ordre n’est pas accessible
à l’utilisateur, c’est un élément privé.
- Le modèle
mathématique choisi est la suite finie d’éléments
de type T0 :
(ai)iÎI où I est fini, totalement
ordonné, ai Î T0
- La pile possède
une place spéciale dénommée sommet qui identifie
son premier élément et contient toujours le dernier élément
entré.
- Le nombre d’éléments
d’une pile LIFO P est appelé profondeur de la pile. Si la pile
est vide nous dirons que sa profondeur est nulle (profondeur = 0 ).
- On doit pouvoir effectuer
sur une pile LIFO au minimum (non exhaustif) les actions suivantes : voir
si la pile est vide, dépiler un élément,
empiler un élément, observer le premier
élément sans le prendre, etc...
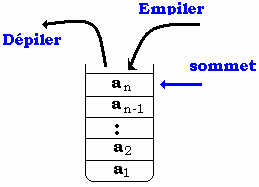
- C’est une structure
de donnée séquentielle dans laquelle les données peuvent
être traitées les unes à la suite des autres à
partir du sommet.
Ecriture syntaxique
du TAD Pile LIFO
TAD PILIFO
utilise
: T0, Booléens
Champs
: (a1,.....,an) suite finie dans T0
opérations
:
sommet :
¾® PILIFO
Est_vide : PILIFO ¾® Booléens
empiler : PILIFO x T0
x sommet ¾® PILIFO x sommet
dépiler : PILIFO x sommet
¾® PILIFO x sommet x T0
premier : PILIFO ¾® T0
préconditions
:
dépiler(P) def_ssi
est_vide(P) = Faux
premier(P) def_ssi
est_vide(P) = Faux
FinTAD-PILIFO
spécification
opérationnelle concrète
- La Pile est représentée
en mémoire dans un tableau.
- Le sommet
(noté top) de la pile est un pointeur sur la case du tableau
contenant le début de la pile. Les variations du contenu k de top
se font au gré des empilements et dépilements.
- Le tableau est plus
grand que la pile (il y a donc dans cette interprétation une contrainte
sur la longueur, notons Longmax cette valeur maximale de profondeur
de la pile).
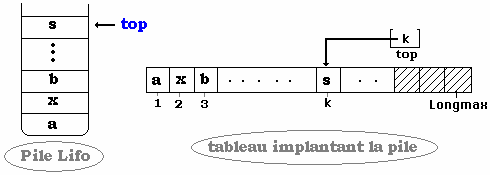
- L’opérateur
empiler : rajoute dans le tableau dans la case pointée
par top un élément et top augmente d’une unité.
- L’opérateur
depiler : renvoie l’élément pointé par
top et diminue top d’une unité.
- L’opérateur
premier fournit une copie du sommet pointé par top (la
pile reste intacte).
- L’opérateur
Est_vide teste si la pile est vide (vrai si elle est
vide, faux sinon).
1.7 Le TAD file FIFO (spécification
abstraite seule)
 LearnP.dif
LearnP.dif
Spécification
abstraite
Répertorions les fonctionnalités d’une file FIFO (First
In First Out) en soulignant les verbes d'actions et les noms, à partir
d’une description semi-formalisée:
- C’est un modèle
pour toute structure de données où l’on accumule des informations
les unes après les autres, mais où l’on choisit d’effectuer
un traitement selon l’ordre d’arrivée des éléments, comme
dans une file d’attente.
- Exemples :toutes
les files d’attente, supermarchés, cantines , distributeurs de pièces,
etc...
- Il est possible dans
une telle structure d’ajouter des éléments à
la fin de la file, ou de retirer des éléments uniquement
au début de la file.
- L’ordre des
éléments est imposé par la file. Cet ordre est construit
non sur la valeur des éléments de la liste, mais sur les places
(rangs)de ces éléments dans la liste. Cet ordre n’est pas accessible
à l’utilisateur, c’est un élément privé.
- Le modèle
mathématique choisi est la suite finie d’éléments
de type T0 :
(ai)iÎI où I est fini, totalement
ordonné, ai Î T0
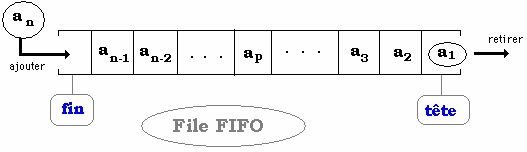
- La file possède deux
places spéciales dénommées tête et fin
qui identifient l’une son premier élément, l’autre le dernier
élément entré.
- Le nombre d’éléments
d’une file FIFO " F " est appelé longueur de la file ; si la
file est vide nous dirons que sa longueur est nulle (longueur = 0 ).
- On doit pouvoir effectuer
sur une file FIFO au minimum (non exhaustif) les actions suivantes : voir
si la file est vide, ajouter un élément, retirer
un élément, observer le premier élément
sans le prendre, etc...
Ecriture syntaxique du
TAD file FIFO
TAD FIFO
utilise
: T0, Booléens
Champs :
(a1,.....,an) suite finie dans T0
opérations
:
tête :
¾® FIFO
fin : ¾® FIFO
Est_vide : FIFO ¾® Booléens
ajouter : FIFO x T0 x
fin ¾® PILIFO x fin
retirer : FIFO x tête ¾® FIFO x tête x T0
premier : FIFO ¾® T0
préconditions
:
retirer(F) def_ssi
est_vide(F) = Faux
premier(F) def_ssi
est_vide(F) = Faux
FinTAD-FIFO
Spécification
opérationnelle concrète
- La file est représentée
en mémoire dans un tableau.
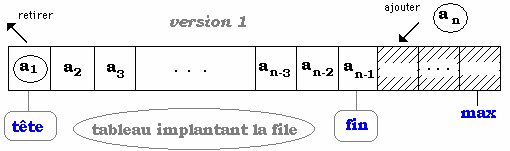
- La tête
de la file est un pointeur sur la case du tableau contenant le début
de la file. Les variations de la valeur de la tête se font au gré
des ajouts et des retraits.
- La fin ne
bouge pas , c’est le point d’entrée de la file.
- Le tableau est plus
grand que la file (il y a donc dans cette interprétation une contrainte
sur la longueur ; notons max cette valeur maximale de longueur de la
file).
- L’opérateur
ajouter : ajoute dans le tableau dans la case pointée
par fin un élément et tête augmente d’une unité.
- L’opérateur
retirer : renvoie l’élément pointé par
tête et diminue tête d’une unité.
- L’opérateur
premier fournit une copie de l’élément pointé
par tête (la file reste intacte).
- L’opérateur
Est_vide teste si la file est vide (vrai si elle est vide, faux
sinon).
On peut ajouter après
la dernière cellule pointée par l'élément fin
comme le montre la figure ci-dessous :
dans ce cas retirer un élément
en tête impliquera un décalage des données vers la gauche.
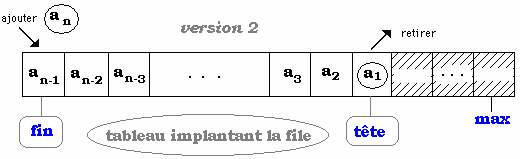
On peut aussi choisir d'ajouter à partir de la première cellule
comme le montre la figure ci-dessous :
dans ce cas ajouter un élément en fin impliquera un décalage
des données vers la droite.
2. Types abstraits de données et Unités en
pascal-Delphi
Nous allons proposer une écriture
des TAD avec des unités pascal (version
avec Unit) puis plus tard avec des objets Delphi.
La notion d’unité (Unit)
se situe au niveau 4 de la hiérarchie informationnelle citée
plus haut : elle nous a déjà servi à implanter la notion
de module. Une unité est donc une approximation relativement bonne
pour le débutant de la notion de TAD. Les classes se situant au niveau
2 de cette hiérarchie constitueront une meilleure approche de cette
notion.
En fait un TAD sera bien décrit
par la partie interface d’une unit et se traduit presque immédiatement
; le travail de traduction des préconditions est à la charge
du programmeur et se trouvera dans la partie privée de la unit
(implementation)
2.1 Traduction générale
TAD ®
Unit pascal
| syntaxe du TAD |
squelette de la unit associée |
| TAD Truc |
Unit Truc ; |
| utilise
TAD1 , TAD2,...,TADn
|
interface
uses TAD1,...,TADn ;
|
champs
........
|
const ....
type ....
var ....
|
| opérations
Op1 : E x F à
G
Op2 : E x F x G à
H x S
............
|
procedure
Op1(x :E ;y :F ;var z :G) ;
procedure Op2(x :E ;y :F ; z :G ;
var t :H ;var u :S) ;
............
|
| FinTAD-Truc |
end. |
Le programmeur n’a plus qu’a écrire
dans la partie implementation de la unit les blocs de code associés
à chacune des procédures décrites dans la partie interface
:
Unit Truc ;
interface
............
implementation
procedure Op1(x
:E ;y :F ;var z :G) ;
begin
............
end ;
procedure Op2(x
:E ;y :F ; z :G ;
var t :H ;var u :S) ;
begin
............
end ;
etc...
end.
2.2 Exemples de Traduction
TAD ®
Unit pascal
Le TAD Booléens implanté sous
deux spécifications concrètes en pascal avec deux type scalaires
différents.
TAD : Booléens
Champs :
Opérations
:
Vrai : ¾® Booléens
Faux : ¾® Booléens
Et : Booléens x Booléens
¾® Booléens
Ou : Booléens x Booléens
¾® Booléens
Non : Booléens ¾® Booléens
FINTAD-Booléens
Spécification
opérationnelle concrète n°1
Les constantes du type
Vrai, Faux sont représentées par deux constantes pascal dans
un type intervalle sur les entiers.
Const
vrai=1 ; faux=0
type
Booleens=faux..vrai
;
Voici l’interface de
la unit traduite de ce TAD :
Unit Bool ;
interface
Const
vrai=1 ; faux=0
type
Booleens=faux..vrai
;
function Et
(x,y :Booleens) :Booleens ;
function Ou (x,y
:Booleens) :Booleens ;
function Non(x :Booleens)
:Booleens ;
Spécification
opérationnelle concrète n°2
Les constantes du type
Vrai, Faux sont représentées par deux identificateurs pascal
dans un type énuméré.
type
Booleens=(faux,vrai)
;
Voici l’interface de
la unit traduite de ce TAD :
Unit Bool ;
interface
type
Booleens=(faux,vrai)
;
function Et
(x,y :Booleens) :Booleens ;
function Ou (x,y
:Booleens) :Booleens ;
function Non(x :Booleens)
:Booleens ;
2.3 Variations sur les spécifications
d’implantation
Cet exercice ayant été
proposé à un groupe d’étudiants, nous avons eu plusieurs
genres d’implantation des opérations : et,ou,non. Nous exposons au
lecteur ceux qui nous ont parus être les plus significatifs :
Implantation d’après
spécification concrète n°1
implementation
function Et
(x,y :Booleens) :Booleens ;
begin
Et := x * y
end ;
function Ou
(x,y :Booleens) :Booleens ;
begin
Ou :=x+y - x*y
end ;
function Non(x
:Booleens) :Booleens ;
begin
Non := 1-x
end ;
L’analyse des étudiants
a été dirigée ici par le choix de la spécification
concrète sur les entiers sur un modèle semblable aux fonctions
indicatrices des ensembles. Ils ont alors cherché des combinaisons
simples d’opérateurs sur les entiers fournissant les valeurs adéquates.
Autre implantation
d’après la même spécification concrète
implementation
function Et
(x,y :Booleens) :Booleens ;
begin
if x=Faux
then Et :=Faux
else Et :=
Vrai
end ;
function Ou
(x,y :Booleens) :Booleens ;
begin
if x=Vrai
then Ou := Vrai
else Ou :=
Faux
end ;
function Non(x
:Booleens) :Booleens ;
begin
if x=Vrai
then Non := Faux
else Non
:= Vrai
end ;
L’analyse des étudiants
a été dirigée dans ce cas par des considérations
axiomatiques sur une algèbre de Boole. Ils se sont servis des propriétés
d’absorbtion des éléments neutres de la loi " ou " et
de la loi " et ". Il s’agit là d’une structure algébrique
abstraite.
Influence de l’abstraction
sur la réutilisation
A cette étape
du travail nous avons demandé aux étudiants quel était,
s’il y en avait un, le meilleur choix d’implantation quant à sa réutilisation
pour l’implantation d’après la spécification concrète
n°2.
Les étudiants
ont compris que la version dirigée par les axiomes l’emportait sur
la précédente, car sa qualité d’abstraction due à
l’utilisation de l’axiomatique a permis de la réutiliser sans aucun
changement dans la partie implementation de la unit associée à
spécification concrète n°2 (en fait toute utilisation des
axiomes d’algèbre de Boole produit la même efficacité).
Conclusion :
| l’abstraction a
permis ici une réutilisation totale et donc un gain de temps de programmation
dans le cas où l’on souhaite changer quelle qu’en soit la raison, la
spécification concrète. |
Dans les exemples qui
suivent, la notation @ indique
la traduction en un squelette en langage pascal.
2.4 Exemples d’implantation
de la liste linéaire
spécification proposée en pseudo-Pascal :
| Liste @ |
type Liste=record
t : array[1..
Longmax] of T0;
long : 0.. Longmax
end;
|
| liste_vide
@ |
var L : Liste (avec
L.long :=0) |
| acces @ |
var k : integer;
L : liste (adresse(L.t[k])) |
| contenu @ |
var k : integer;
L : liste (val(adresse(L.t[k]))) |
| kème
@ |
var k : integer;
L : liste (kème(L,k)
@ L.t[k] ) |
| long @ |
var L : liste (
long @ L.long ) |
| succ @ |
adresse(L.t[k])+1 c-à-dire
( L.t[k+1] ) |
| supprimer
@ |
procedure supprimer(var
L : Liste ; k : 1.. Longmax);
begin
..........
end; {supprimer} |
| inserer @ |
procedure inserer(var
L : Liste ; k : 1.. Longmax; x : T0);
begin
..........
end; {inserer} |
- La précondition de
l’opérateur supprimer peut être ici implantée par le
test
- La précondition de
l’opérateur insérer peut être ici implantée par
le test
if (long(L) < Longmax)
and (k<=Long(L)+1) then .....
- Les deux objets acces et
contenu ne seront pas utilisés en pratique, car le tableau les implante
automatiquement d’une manière transparente pour le programmeur.
Le reste du programme est laissé
au soin du lecteur qui pourra ainsi se construire sur sa machine ,une base
de types en Pascal.
 LearnP.dif
LearnP.dif
Nous pouvons " enrichir
" le TAD Liste en lui adjoignant deux opérateurs test et rechercher
(rechercher un élément dans une liste). Ces adjonctions ne posent
aucun problème. Il suffit pour cela de rajouter au TAD les lignes
correspondantes :
opérations
Test : Liste x T0 ¾® Booléen
rechercher : Liste x T0 ¾® Place
précondition
rechercher(L,e)
def_ssi Test(L,e) = V
Le lecteur construira à
titre d’exercice l’implantation Pascal de ces deux nouveaux opérateurs
en étendant le programme Pascal déjà construit. Il pourra
par exemple se baser sur le schéma de représentation Pascal
suivant :
function Test(L : liste;
e : T0):Boolean;
begin
{il s’agit
de tester la présence ou non de e dans la liste L}
end;
procedure rechercher(L
: liste ; x : T0; var rang : integer);
begin
if Test(L,x) then
{il
s’agit de fournir le rang de x dans la liste L}
else
end;
2.5 Exemples d’implantation
de la pile LIFO
spécification
proposée en pseudo-Pascal :
Nous allons utiliser un tableau
avec une case supplémentaire permettant d’indiquer que le fond de pile
est atteint (la case 0 par exemple, qui ne contiendra jamais d’élément).
| Pilifo @ |
type Pilifo=record
t : array[ 0..
Longmax ] of T0;
sommet: 0.. Longmax
end;
|
| depiler @ |
procedure depiler(var
Elt : T0 ;var P : Pilifo) ; |
| empiler @ |
procedure empiler(
Elt : T0 ;var P : Pilifo) ; |
| premier @ |
procedure premier(var
Elt : T0 ; P : Pilifo) ;
(on pourra utiliser une function renvoyant un T0, si
le type T0 s’y prête !) |
| Est_vide
@ |
function Est_vide(P
: Pilifo) : boolean ; |
Le contenu des procédures
et des fonctions est laissé au lecteur à titre d’exercice.
 LearnP.dif
LearnP.dif
Remarque
:
| Il est aussi possible de construire
une spécification opérationnelle à l’aide du TAD Liste
en remplaçant dans l’étude précédente le mot "
tableau " par le mot " liste ". Il est vivement conseillé au lecteur
d’écrire cet exercice en pascal pour bien se convaincre de la différence
entre les niveaux d’abstractions. Nous le traiterons plus loin en Delphi. |
2.6 Exemples d’implantation
de la file FIFO
spécification
proposée en pseudo-Pascal :
Nous allons utiliser ici aussi
un tableau avec une case supplémentaire permettant d’indiquer
que la file est vide (la case 0 par exemple, qui ne contiendra jamais d’élément).
| Fifo @ |
type Fifo=record
t : array[ 0..
Longmax ] of T0;
sommet: 0.. Longmax
end;
|
| retirer @ |
procedure retirer(var
Elt : T0 ;var F : Fifo) ; |
| ajouter @ |
procedure ajouter(
Elt : T0 ;var F : Fifo) ; |
| premier @ |
procedure premier(var
Elt : T0 ; P : Fifo) ;
(on
pourra utiliser une function renvoyant un T0, si le type T0
s’y prête !) |
| Est_vide
@ |
function Est_vide(P
: Fifo) : boolean ; |
Le contenu des procédures
et des fonctions est laissé au lecteur à titre d’exercice.
Remarque
:
| Comme pour le TAD Pilifo, il
est aussi possible de construire une spécification opérationnelle
du TAD FIFO à l’aide du TAD Liste en remplaçant dans l’étude
précédente le mot " tableau " par le mot " liste ". |
 PanneauTAD.dif
PanneauTAD.dif