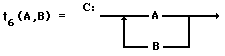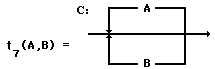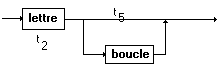4.5.TAD et spécification graphique


Plan du chapitre:

1. Application des TAD à la construction d’analyseur

     
    1.1 Un TAD générique de grammaire graphique
     


2.Exemples d’instanciation de ce TAD générique

     
    2.1 Les identificateurs pascal-like
    2.2 Les expressions arithmétiques
    2.3 Un TAD générateur d’analyseur
     


Voici maintenant dans un tout autre domaine une utilisation intéressante des TAD : il s’agit de la programmation par les grammaires qui fait partie du domaine de la compilation1. Comme exemple, nous allons construire un TAD générique de grammaire graphique, qui pourra être instancié en une grammaire quelconque de diagrammes syntaxiques. Nous nous servirons de ce TAD comme squelette de la construction d’un analyseur, puis ensuite nous verrons un autre TAD dérivé du premier permettant d’obtenir une spécification simple d’un générateur d’analyseur pour grammaire LL(1). Cet exercice part de la remarque que les diagrammes syntaxiques servent à décrire toutes les C-grammaires : ils représentent donc une abstraction générique.

Dans toute la suite les grammaires considérées sont des C-grammaires (type 2).
        1. Application des TAD à la construction d’analyseur
     

    spécification d’un générateur d’analyseur pour grammaire LL(1)
     

       


    1.1 Un TAD générique de grammaire graphique

    Nous avons vu précédemment que les diagrammes syntaxiques sont une représentation graphique des règles d’une grammaire.

    Nous allons établir une spécification fondée sur les diagrammes syntaxiques comme éléments de base, l’ensemble des diagrammes est noté Diag. Une grammaire est parfaitement définie par la donnée de : son vocabulaire terminal VT, son vocabulaire auxiliaire VN et ses diagrammes syntaxiques(ces dernières représentant l’axiome et les règles de cette grammaire).
     

    Nous proposons un type abstrait basé sur 8 opérateurs sur les diagrammes syntaxiques.

    TAD : Diag
    utilise : VT, VN // les vocabulaires de la grammaire

    opérations :

      t1 : à Diag
      t2 : VT È VN à Diag
      t3 : VN à Diag
      t4 : VT È VN à Diag
      t5 : (VT È VN)n à Diag
      t6 : (VT È VN)2 à Diag
      t7 : (VT È VN)2 à Diag
      · : Diag x Diag à Diag
    Axiomes :
      · est associative (concaténation de diagrammes)


    "tiÎ Diag (i ³1) / t1·ti = ti·t1(élément neutre)

    ti(A)·tk(B) = ti(A)tk(B) (méthode de construction des diagrammes)


     
     

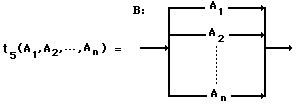
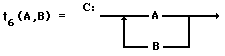
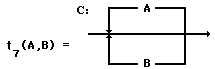
    On rappelle que dans la représentation en diagrammes syntaxiques, que le nom du paragraphe syntaxique A:, B:, C: est un élément du vocabulaire auxiliaire VN. Il correspond à la partie gauche de la règle.
     

    Remarque :
    l’opérateur t7 est redondant car il est possible de l’ exprimer à l’aide des 6 autres, par exemple : t7(B)=t5(t1,t3(t5(A,B))).

     
    2.Exemples d’instanciation de ce TAD générique Diag
     
     

    2.1 Les identificateurs pascal-like
     

    Reprenons une grammaire déjà utilisée auparavant, celle des identificateurs en pascal.
     

    identif :

     

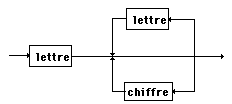
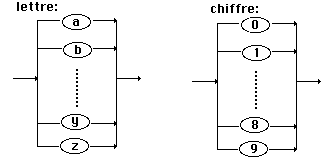
    En utilisant le TAD Diag générique précédent, on obtient à partir des valeurs d’instanciation suivantes:

    VN = { álettreñ, áchiffreñ, áidentifñ }
    VT = { 0,1,....,8,9,a,b,.....,z }

    (seuls VN,VT, et les axiomes changent les autres parties du TAD sont identiques)

    Axiomes :

      áidentifñ = t2(álettreñ) · t7(álettreñ, áchiffreñ)
      álettreñ = t5(a,b,.....,z)
      áchiffreñ = t5(0,1,....,8,9)


    on obtient d’autres axiomes en utilisant la transformation

    t7(B)=t5(t1,t3(t5(A,B)))

    Axiomes :

      áidentifñ = t2(álettreñ) · t5(ásortieñ, áboucleñ)
      ásortieñ = t1
      áboucleñ = t3(áinterneñ)
      áinterneñ = t5(álettreñ,áchiffreñ)
      álettreñ = t5(a,b,.....,z)
      áchiffreñ = t5(0,1,....,8,9)


    avec : VN ={álettreñ,áchiffreñ,áidentifñ,áinterneñ,ásortieñ,áboucleñ}

    Ce dernier TAD correspond à une autre expression d’une grammaire des identificateurs pascal :

    áidentifñ :                  áboucleñ :

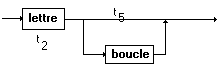
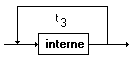
    áinterneñ :

     

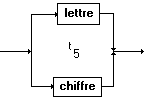
    Les deux autres diagrammes de <lettre> et <chiffre> sont les mêmes que les précédents.
     
     

    2.2 Les expressions arithmétiques

    Soit une grammaire des expressions :

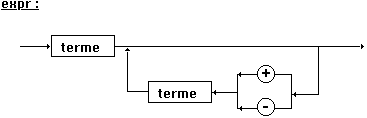
    Nous obtenons pour <expr> :
    áexprñ = t2(átermeñ) · t4(t5(‘+’,‘-‘ )· t2(átermeñ))
     

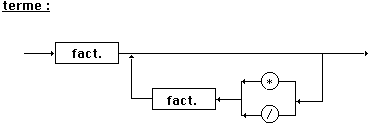
    De même pour átermeñ :
    átermeñ = t2(áfactñ) · t4(t5(‘*’,’/’)· t2(áfactñ))
     

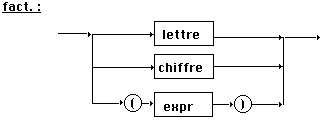
    Enfin pour áfactñ les combinaisons d’opérateurs sont :
    áfactñ = t5(álettreñ,áchiffreñ,t2(‘(‘)· t2(áexprñ)· t2(‘)‘))
     
     


    Pour áchiffreñ et álettreñ mêmes opérateurs que plus haut.
     

    Nous laissons le soin au lecteur d’écrire à l’aide du TAD Diag et des opérateurs fournis, les axiomes du TAD grammaire graphique correspondant aux expressions.
     
     

2.3 Un TAD générateur d’analyseur

A partir du TAD Diag de grammaire graphique, nous proposons d’écrire un TAD GenerAnalyse permettant de générer manuellement des squelettes pascal permettant d’analyser chacun des opérateurs de Diag.
 

TAD : GenerAnalyse
utilise : Diag(instancié Pascal),Pascal
opérations :

Init :®Pascal
sym :®Pascal
symsuiv :®Pascal
Err :®Pascal
Trad : Diag®Pascal
Follow :®Pascal préconditions : trad(t2(A)) def_ssi sym ÎInit(A)
trad(t3(A)) def_ssi sym ÎInit(A)
trad(t4(A,B)) pas de précondition
trad(t5(A1,...,An)) def_ssi sym Î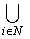Init(Ai)
trad(t6(A,B)) def_ssi sym ÎInit(A)
trad(t7(A,B)) pas de précondition


Axiomes(de traduction):
 
trad(t1)@ if not sym in Follow(A) then Err;
trad(t2(A)) @ si A ÎVN alors : if sym in Init(A) then
begin
A ;
if not(sym in Follow(A) then Err
end
else Err
trad(t2(A))@ si A ÎVT alors : if sym=A then symsuiv else Err
trad(t3(A)) @ si A ÎVN alors : repeat
A ;
if not sym in Follow(A) then Err
until not(sym in Init(A));
trad(t3(A))@ si A ÎVT alors : repeat
symsuiv;
until sym <>A ;
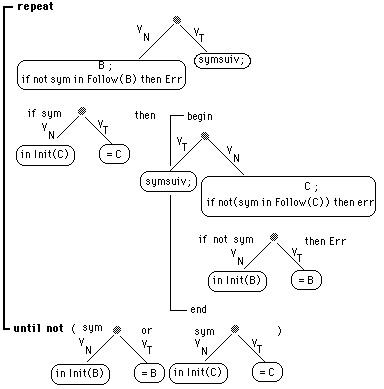
trad(t6(B,C))@ selon que B ou C sont dans VT ou dans VN :
trad(t4(A)) @ si A ÎVT alors : if sym=A then
while sym=A do symsuiv
else if not sym in Follow(B) then Err
trad(t4(A)) @ si A ÎVN alors : if sym=A then
while sym in Init(A) do begin
A ;
if not sym in Follow(A) then Err
end
else if not sym in Follow(B) then Err
trad(t5(A1,...,An))@ soit Ai ÎVN et Aj ÎVT alors : ..........
if sym in Init(Ai) then
begin
Ai ;
if not sym in Follow(Ai) then Err
end else
..........
if sym=Aj then symsuiv
..........
else Err
trad(t7(A,B))@ si A ÎVT alors : if sym=A then
while sym=A do symsuiv
else if not sym in Follow(B) then Err
trad(t7(A,B)) @ si A ÎVN alors : if sym=A then
while sym in Init(A) do begin
A ;
if not sym in Follow(A) then Err
end
else if not sym in Follow(B) then Err

Application - exercice

Ecrivez et programmez l’analyseur engendré par le TAD GenerAnalyse défini précédemment instancié sur la grammaire des identificateurs Pascal-like. Pour vous aider, voici une partie des déclarations ce ce programme:
 

VN = { álettreñ,áchiffreñ,áidentifñ }
VT = { 0,1,....,8,9,a,b,.....,z }
 

Axiomes :
áidentifñ = t2(<lettreñ)· t7(álettreñ,áchiffreñ)
álettreñ = t5(a,b,.....,z)
áchiffreñ = t5(0,1,....,8,9)

  program analyse_identif;
{ le mot à analyser est dans chaine }
type Vt=char ;
var init_identif,init_lettre,init_chiffre : set of char;
follow_lettre,follow_chiffre : set of char;
sym : Vt;
erreur : boolean;
numcar : integer;
chaine : string;


procedure init;
begin

numcar:=0;
erreur:=false end;

procedure symsuiv;
begin

numcar:=numcar+1;
sym:=chaine[numcar] end;

procedure Err(num:integer);
begin

writeln(‘Erreur n°’,num);
erreur:=true;
halt end;

procedure init_ens;
begin

init_lettre:=[‘a’..’z’];
init_chiffre:=[‘0’..’9’];
follow_lettre:=init_lettre+init_chiffre;
follow_chiffre:=follow_lettre end;

procedure identif;forward;
procedure lettre;forward;
procedure chiffre;forward;

{<identif> = t2(<lettre>) · t7(<lettre>,<chiffre>)}
procedure identif;
begin

if sym in Init(A) thenbegin
A ;
If not(sym in Follow(A) then Err
end
else Err ;
symsuiv; end;

procedure lettre;
begin

????????
{cherchez le bon trad(ti.....} end;

procedure chiffre;
begin

????????
{cherchez le bon trad(ti.....} end;

begin{prog-principal}

init;
init_ens;
Write(‘Entrez un identificateur:’);
readln(chaine);
chaine:=concat(chaine,’.’); {car lecture un symbole plus loin}
symsuiv;
identif;
if not erreur then writeln('Identif reconnu')
else writeln('Identif non conforme') end.