Arbres binaires
Plan du chapitre:
1. Notions générales sur les arbres
La structure d'arbre est très utilisée en informatique. Sur
le fond on peut considérer un arbre comme une généralisation
d'une liste car les listes peuvent être représentées par
des arbres. La complexité des algorithmes d'insertion de suppression
ou de recherche est généralement plus faible que dans le cas
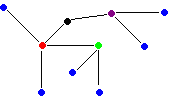
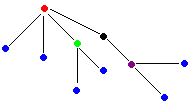
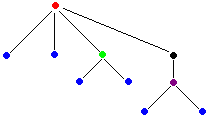
des listes ( cas particulier des arbres équilibrés). Les mathématiciens
voient les arbres eux-même comme des cas particuliers de graphes non
orientés connexes et acycliques, donc contenant des sommets et des
arcs :
|
|
|
Enfin certains arbres particuliers nommés arbres binaires sont les
plus utilisés en informatique et les plus simples à étudier.
En outre il est toujours possible de "binariser" un arbre non binaire,
ce qui nous permettra dans ce chapitre de n'étudier que les structures
d'arbres binaires.
1.1 Vocabulaire employé sur les arbres
Un arbre dont tous les noeuds sont nommés est dit étiqueté. L'étiquette (ou nom du sommet) représente la "valeur" du noeud ou bien l'information associée au noeud. Ci-dessous un arbre étiqueté dans les entiers entre 1 et 10 :
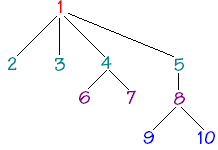
Nous rappellons la terminologie de base sur les arbres sur le schéma ci-dessous :
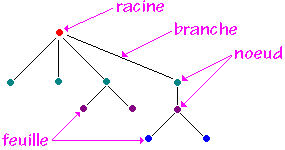
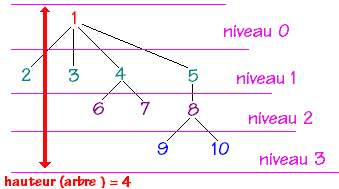
Nous conviendrons de définir la hauteur(ou profondeur ou niveau ) d'un noeud X comme égale au nombre de noeuds à partir de la racine pour aller jusqu'au noeud X. En reprenant l'arbre précédant et en notant h la fonction hauteur d'un noeud :
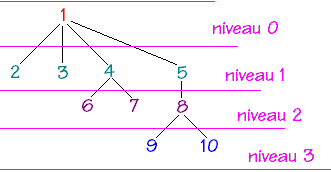
Pour atteindre le noeud étiqueté 9 , il faut parcourir le lien 1--5, puis 5--8, puis enfin 8--9 soient 4 noeuds donc 9 est de profondeur ou de hauteur égale à 4, soit h(9) = 4.
Pour atteindre le noeud étiqueté 7 , il faut parcourir le
lien 1--4, et enfin 4--7, donc 7 est de profondeur ou de hauteur égale
à 3, soit h(7) = 3.
| Par définition la hauteur de la racine est égal à
1. h(racine) =1 (pour tout arbre non vide) |
(Certains auteurs adoptent une autre convention pour calculer la hauteur d'un noeud: la racine a pour hauteur 0 et donc n'est pa comptée dans le nombre de noeuds, ce qui donne une hauteur inférieure d'une unité à notre définition).
On appelle chemin du noeud X la suite des noeuds par lesquels il faut passer pour aller de la racine vers le noeud X :

Chemin du noeud 10 = (1,5,8,10)
Chemin du noeud 9 = (1,5,8,9)
.....
Chemin du noeud 7 = (1,4,7)
Chemin du noeud 5 = (1,5)
Chemin du noeud 1 = (1)
Remarquons que la hauteur h d'un noeud X est égale au nombre de
noeuds dans le chemin :
| h( X ) = NbrNoeud( Chemin( X ) ). |
Le vocabulaire de lien entre noeuds de niveaux différents et reliés
entres eux est emprunté à la généalogie :
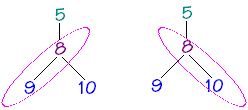
9 est l'enfant de 8 10 est l'enfant de 8 8 est le parent de 9 10 est le parent de 8 |
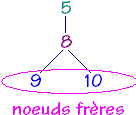
9 et 10 sont des frères |
5 est le parent de 8 et l'ancêtre de 9 et 10.
On parle aussi d'ascendant, de descendant ou de fils pour évoquer des relations entres les noeuds d'un même arbre reliés entre eux.
Nous pouvons définir récursivement la hauteur h d'un noeud
X à partir de celle de son parent :
| h (racine) = 1; h ( X ) = 1+ h ( parent ( X ) ) |
Reprenons l'arbre précédent en exemple :

Calculons récursivement la hauteur du noeud 9, notée h(9) :
h(9) = 1+h(8)
h(8) = 1+h(5)
h(5) = 1+h(1)
h(1) = 1 => h(5)=2 => h(8)=3 => h(9)=4
Par définition le degré
d'un noeud est égal au nombre de ses descendants
(enfants). Soient les deux exemples ci-dessous extraits de l'arbre précédent
:
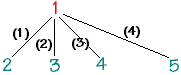
Le noeud 1 est de degré 4, car il a 4 enfants
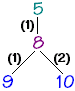
Le noeud 5 n'ayant qu'un enfant son degré est 1.
Le noeud 8 est de degré 2 car il a 2 enfants.
Remarquons que lorsqu'un arbre a tous ses noeuds de degré 1, on le nomme arbre dégénéré et que c'est en fait une liste.
Par définition c'est le nombre de noeuds
du chemin le plus long dans l'arbre. La hauteur h d'un arbre
correspond donc au nombre de niveau maximum :
|
si Arbre = Æ alors h( Arbre ) = 0 |
La hauteur de l'arbre ci-dessous :
Le degré d'un arbre est égal au plus grand des degrés de ses noeuds :
|
|
Soit à répertorier dans l'arbre ci-dessous le degré
de chacun des noeuds :

|
d°(1) = 4 d°(2) = 0 d°(3) = 0 d°(4) = 2 d°(5) = 1 d°(6) = 0 d°(7) = 0 d°(8) = 2 d°(9) = 0 d°(10) = 0 |
On appelle taille d'un arbre le nombre
total de noeuds de cet arbre :
|
|

Cet arbre a pour taille 10 (car il a 10 noeuds)
Arbre
de dérivation d'un mot dans une grammaire (chap 2.3)
|
arbre d'analyse |
Soit la grammaire
G2 : VN = {S}
VT = {( , )}
Axiome : S
Règles
1 :
S ¾® (SS)S
2 : S ¾® e
Le langage L(G2) se dénomme langage des parenthèses bien formées.
Soit le mot (( )) de G2 , voici un arbre de dérivation
de (( )) dans G2 :
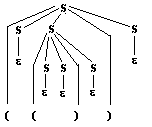
|
arbre abstrait |
Soit la grammaire Gexp :
| Gexp
= (VN,VT,Axiome,Règles)
VT = { 0, ..., 9,
+,-, /, *, ), (} |
soit : 327 - 8 un mot de L(Gexp)
Soit son arbre de dérivation dans Gexp :
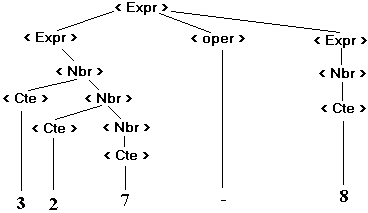
L’arbre obtenu ci-dessous en
grisé à partir de l’arbre de dérivation s’appelle l’arbre
abstrait du mot " 327-8 " :
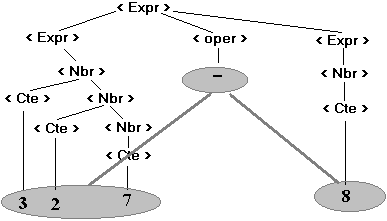
On note ainsi cet arbre abstrait :
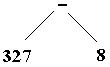
Voici d'autres abres abstraits d'expressions arithmétiques :
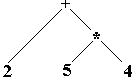
expr = 2 + 5*4 |
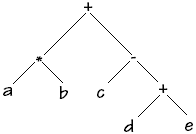
expr = a*b + c-(d+e) |
Rangement de mots par ordre lexical (alphabétique)
Soient les mots BON, BONJOUR, BORD, BOND, BOREALE, BIEN, il est possible de les ranger ainsi dans une structure d'arbre :
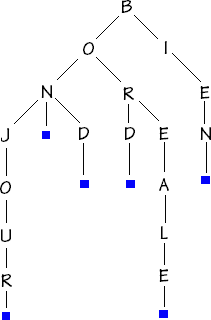
Cet arbre se dénomme un arbre lexicographique.
Voici à titre d'exemple que nous étudierons plus loin en détail, un arbre dont les noeuds sont de degré 2 au plus et qui est tel que pour chaque noeud la valeur de son enfant de gauche lui est inférieure ou égale, la valeur de son enfant de droite lui est strictement supérieure.
Ci-dessous un tel arbre ayant comme racine 30 et stockant des entiers selon cette répartition :
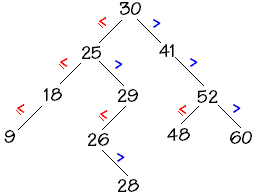
2. Les arbres binaires
Un arbre binaire est un arbre de degré 2 (dont les noeuds sont de degré 2 au plus).
L'arbre abstrait de l'expression a*b + c-(d+e) est un arbre binaire :

Vocabulaire :
Les descendants (enfants) d'un noeud sont lus de gauche à droite et sont appelés respectivement fils gauche (descendant gauche) et fils droit (descendant droit) de ce noeud.
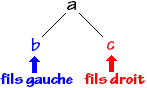
Les arbres binaires sont utilisés dans de très nombreuses activités informatiques et comme nous l'avons déjà signalé il est toujours possible de reprrésenter un arbre général (de degré >2 ) par un arbre binaire en opérant une "binarisation".
Nous allons donc étudier dans la suite, le comportement de cette structure de données récursive.
Afin d'assurer une cohérence avec les autres structures de données déjà vues (liste, pile, file) nous proposons de décrire une abstraction d'un arbre binaire avec un TAD. Soit la signature du TAD d'arbre binaire :
TAD ArbreBin
utilise : T0, Noeud, Booleens
opérations :
Æ : ¾® ArbreBi Racine : ArbreBin ¾® Noeud filsG : ArbreBin ¾® ArbreBin filsD : ArbreBin ¾® ArbreBin Constr : Noeud x ArbreBin x ArbreBin ¾® ArbreBin Est_Vide : ArbreBin ¾® Booleens Info : Noeud ¾® T0
préconditions :
Racine(Arb) def_ssi Arb ¹ Æ filsG(Arb) def_ssi Arb ¹ Æ filsD(Arb) def_ssi Arb ¹ Æ
axiomes :
"rac Î Noeud , "fg Î ArbreBin , "fd Î ArbreBin Racine(Constr(rac,fg,fd)) = rac filsG(Constr(rac,fg,fd)) = fg
filsD(Constr(rac,fg,fd)) = fd
Info(rac) ÎT0FinTAD-PILIFO
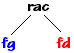
L'opérateur filsG( ) renvoie le sous-arbre gauche de l'arbre binaire, l'opérateur filsD( ) renvoie le sous-arbre droit de l'arbre binaire, l'opérateur Info( ) permet de stocker des informations de type T0 dans chaque noeud de l'arbre binaire.Nous noterons < rac, fg , fd > avec conventions implicites un arbre binaire dessiné ci-dessous :
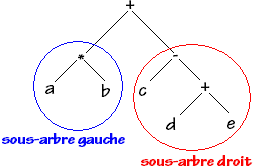
Exemple, soit l'arbre binaire A :
A = 
Les sous-arbres gauche et droit de l'arbre A :
filsG( A ) = < * , a , b >
filsD( A ) = < - , c , < + , d , e > >
2.2 Exemples et implémentation d'arbre binaire étiqueté
Nous proposons de représenter un arbre binaire étiqueté selon deux spécifications différentes classiques :
1°) Une implantation fondée sur une structure de tableau en allocation de mémoire statique, nécessitant de connaître au préalable le nombre maximal de noeuds de l'arbre (ou encore sa taille).
2°) Une implantation fondée sur une structure d'allocation de mémoire dynamique implémentée soit par des pointeurs (variables dynamiques) soit par des références (objets) .
2.2.1 - Implantation dans un tableau statique
Spécification concrète
Un noeud est une structure statique contenant 3 éléments :
- l'information du noeud
- le fils gauche
- le fils droit
Pour un arbre binaire de taille = n, chaque noeud de l'arbre binaire est stocké dans une cellule d'un tableau de dimension 1 à n cellules. Donc chaque noeud est repéré dans le tableau par un indice (celui de la cellule le contenant).Le champ fils gauche du noeud sera l'indice de la cellule contenant le descendant gauche, et le champ fils droit vaudra l'indice de la cellule contenant le descendant droit.
Exemple
Soit l'arbre binaire ci-après :
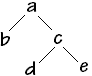
Selon l'implantation choisie, par hypothèse de départ, la racine <a, vers b, vers c> est contenue dans la cellule d'indice 2 du tableau, les autres noeuds sont supposés être rangés dans les cellules 1, 3,4,5 :
racine = table[2]
table[1] = < d , 0 , 0 >
table[2] = < a , 4 , 5 >
table[3] = < e , 0 , 0 >
table[4] = < b , 0 , 0 >
table[5] = < c , 1 , 3 >
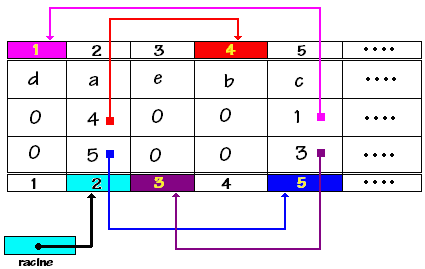
Explications :
table[2] = < a , 4 , 5 > signifie que le fils gauche de ce noeud est dans table[4] et son fils droit dans table[5]
table[5] = < c , 1 , 3 > signifie que le fils gauche de ce noeud est dans table[1] et son fils droit dans table[3]
table[1] = < d , 0 , 0 > signifie que ce noeud est une feuille
...etcSpécification d'implantation en Pascal
Nous proposons d'utiliser les déclarations suivantes :
const
taille = n; // n valeur effective 10, 1000, 10000 etc...
type
Noeud = record
info : T0;
filsG , filsD : 0..taille ;
end;
Tableau = Array[1..taille] of Noeud ;ArbrBin = record
ptrRac : 0..taille;
table : Tableau ;
end;
Var
Tree : ArbrBin ;
Explications :
Lorsque Tree.ptrRac = 0 on dit que l'arbre est vide.
L'accès à la racine de l'arbre s'effectue ainsi : Tree.table[ptrRac]
L'accès à l'info de la racine de l'arbre s'effectue ainsi : Tree.table[ptrRac].info
L'accès au fils gauche de la racine de l'arbre s'effectue ainsi :
var
ptr:0..taille ;
ptr := Tree.table[ptrRac].filsG;
Tree.table[ptr] ....
L'insertion ou la suppression d'un noeud dans l'arbre ainsi représenté s'effectue directement dans une cellule du tableau. Il faudra donc posséder une structure (de liste, de pile ou de file par exemple) permettant de connaître les cellules libres ou de ranger une cellule nouvellement libérée. Une telle structure se dénomme "espace libre".
L'insertion se fera dans la première cellule libre, l'espace libre diminuant d'une unité.
La suppression rajoutera une nouvelle cellule dans l'espace libre qui augmentera d'une unité.
2.2.2 - Implantation avec des variables dynamiques
Spécification concrète
Le noeud reste une structure statique contenant 3 éléments dont 2 sont dynamiques :
Exemple
- l'information du noeud
- une référence vers le fils gauche
- une référence vers le fils droit
Soit l'arbre binaire ci-après :

Selon l'implantation choisie, par hypothèse de départ, la référence vers la racine pointe vers la structure statique (le noeud) < a, ref vers b, ref vers c >
ref racine ® < a, ref vers b, ref vers c >
ref vers b ® < b, null, null >
ref vers c ® < a, ref vers d, ref vers e >
ref vers d ® < d, null, null >
ref vers e ® < e, null, null >
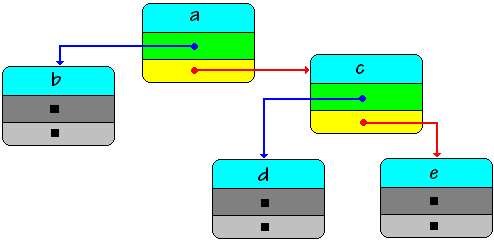
Spécification d'implantation en Pascal
Nous proposons d'utiliser les déclarations de variables dynamiques suivantes :
type
ArbrBin = ^Noeud ;
Noeud = record
info : T0;
filsG , filsD : ArbrBin ;
end;
Var
Tree : ArbrBin ;Explications :
Lorsque Tree = nil on dit que l'arbre est vide.
L'accès à la racine de l'arbre s'effectue ainsi : Tree
L'accès à l'info de la racine de l'arbre s'effectue ainsi : Tree^.info
L'accès au fils gauche de la racine de l'arbre s'effectue ainsi : Tree^.filsG
L'accès au fils gauche de la racine de l'arbre s'effectue ainsi : Tree^.filsDNous noterons une simplification notable des écritures dans cette implantation par rappoprt à l'implantation dans un tableau statique. Ceci provient du fait que la structure d'arbre est définie récursivement et que la notion de variable dynamique permet une définition récursive donc plus proche de la structure.
2.2.3 - Implantation avec une classe
Nous livrons ci-dessous une écriture de la signature et l'implementation minimale d'une classe d'arbre binaire nommée TreeBin en Delphi (l'implementation complète est à faire lors des exercices sur les classes) :
interface
// dans cette classe tous les champ sont publics afin de simplifier l'écriture
TreeBin = class
public
Info : string;
filsG , filsD : TreeBin;
constructor CreerTreeBin(s:string);overload;
constructor CreerTreeBin(s:string; fg , fd : TreeBin);overload;
destructor Liberer;
end;implementation
......
end.
2.3 Arbres binaires de recherche
- Nous avons étudié au chap4.6 des algorithmes de recherche en table, en particulier la recherche dichotomique dans une table triée dont la recherche s'effectue en O(log(n)) comparaisons.
- Toutefois lorsque le nombre des éléments varie (ajout ou suppression) ces ajouts ou suppressions peuvent nécessiter des temps en O(n).
- En utilisant une liste chaînée qui approche bien la structure dynamique (plus gourmande en mémoire qu'un tableau) on aura en moyenne des temps de suppression ou de recherche au pire de l'ordre de O(n). L'ajout en fin de liste ou en début de liste demandant un temps constant noté O(1).
Les arbres binaires de recherche sont un bon compromis pour un temps équilibré entre ajout, suppression et recherche.
Un arbre binaire de recherche satisfait aux critères suivants :
- L'ensemble des étiquettes est totalement ordonné.
- Une étiquette est dénommée clef.
- Les clefs de tous les noeuds du sous-arbre gauche d'un noeud X, sont inférieures ou égales à la clef de X.
- Les clefs de tous les noeuds du sous-arbre droit d'un noeud X, sont supérieures à la clef de X.
Nous en avons déjà vu un plus haut :

Prenons par exemple le noeud (25) son sous-arbre droit est bien composé de noeuds dont les clefs sont supérieures à 25 : (29,26,28). Le sous-arbre gauche du noeud (25) est bien composé de noeuds dont les clefs sont inférieures à 25 : (18,9).On appelle arbre binaire dégénéré un arbre binaire dont le degré = 1, ci-dessous 2 arbres binaires de recherche dégénérés :

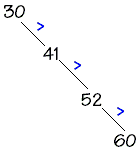
Nous remarquons dans les deux cas que nous avons affaire à une liste chaînée donc le nombre d'opérations pour la suppression ou la recherche est au pire de l'ordre de O(n). Il faudra utiliser une catégorie spéciale d'arbres binaires qui restent équilibrés (leurs feuilles sont sur 2 niveaux au plus) pour assurer une recherche au pire en O(log(n)).
2.4 Arbres binaires partiellement ordonnés (tas)
Arbre parfait :
c'est un arbre binaire dont tous les noeuds de chaque niveau sont présents sauf éventuellement au dernier niveau où il peut manquer des noeuds (noeuds terminaux = feuilles), dans ce cas l'arbre parfait est un arbre binaire incomplet et les feuilles du dernier niveau doivent être regroupées à partir de la gauche de l'arbre. 1 - Un arbre parfait complet :
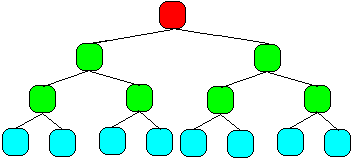
(parfait complet : le dernier niveau est complet car il contient tous les enfants )
2 - Un autre arbre parfait incomplet :
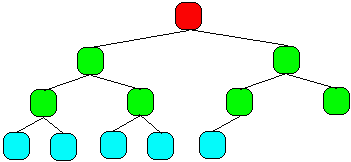
(parfait incomplet : le dernier niveau est incomplet car il manque 3 enfants, mais ils
sont manquant à la droite du niveau, les feuilles sont regroupées à gauche)
3.a - Un arbre non parfait :
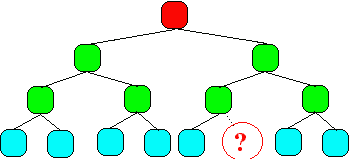
(non parfait : le dernier niveau est incomplet car il manque 1 enfant, les feuilles
ne sont pas regroupées à gauche)3.b - Un autre arbre non parfait :
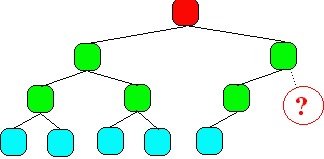
(non parfait : les feuilles sont bien regroupées à gauche, mais
il manque 1 enfant à l'avant dernier niveau )
Un arbre binaire parfait se représente classiquement dans un tableau :
Les noeuds de l'arbre sont dans les cellules du tableau, il n'y a pas d'autre information dans une cellule du tableau, l'accès à la topologie arborescente est simulée à travers un calcul d'indice permettant de parcourir les cellules du tableau selon un certain 'ordre' de numérotation correspondant en fait à un parcours hiérarchique de l'arbre. En effet ce sont les numéros de ce parcours qui servent d'indice aux cellules du tableau :
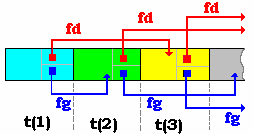
Si t est ce tableau, nous avons donc les règles d'accès suivantes :
- t[1] est la racine :
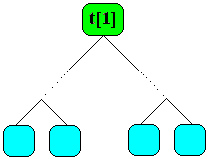
Lorsque l'indice i d'une cellule (d'un noeud) est fixé :
- t[i div 2] est le père de t[i] pour i > 1 :
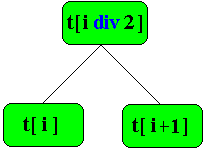
- t[2 * i] et t[2 * i + 1] sont les deux fils, s'ils existent, de t[i] :
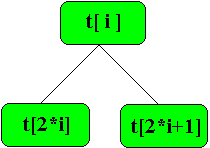
- si p est le nombre de noeuds de l'arbre et si 2 * i = p, t[i] n'a qu'un fils, t[p].
si i est supérieur à p div 2, t[i] est une feuille.
Exemple de rangement d'un tel arbre dans un tableau (pour une vision pédagogique on a figuré l'indice de numérotation hiérarchique de chaque noeud dans le rectangle associé au noeud) :
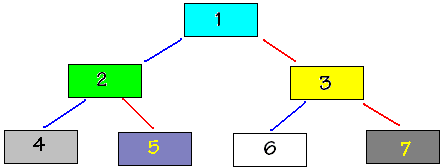
Cet arbre sera stocké dans un tableau en disposant séquentiellement et de façon contigüe les noeuds selon la numérotation hiérarchique (l'index de la cellule = le numéro hiérarchique du noeud).
Dans cette disposition le passage d'un noeud de numéro k (indice dans le tableau) vers son fils gauche s'effectue par calcul d'indice, le fils gauche se trouvera dans la cellule d'index 2*k du tableau, son fils droit se trouvant dans la cellule d'index 2*k + 1 du tableau. Ci-dessous l'arbre précédent est stocké dans un tableau : le noeud d'indice hiérarchique 1 (la racine) dans la cellule d'index 1, le noeud d'indice hiérarchique 2 dans la cellule d'index 2, etc...
Le nombre qui figure dans la cellule (nombre qui vaut l'index de la cellule = le numéro hiérarchique du noeud) n'est mis là qu'à titre pédagogique afin de bien comprendre le mécanisme.
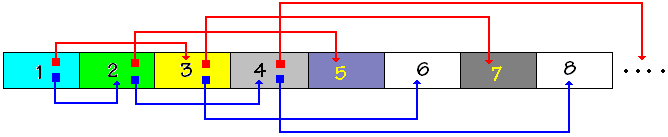
On voit par exemple, que par calcul on a bien le fils gauche du noeud d'indice 2 est dans la cellule d'index 2*2 = 4 et son fils droit se trouve dans la cellule d'index 2*2+1 = 5 ...
Exemple d'un arbre parfait étiqueté avec des caractères :
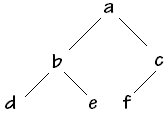
arbre parfait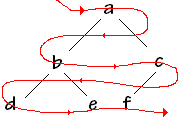
parcours hiérarchique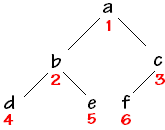
numérotation hiérarchique
rangement de l'arbre
dans un tableauSoit le noeud 'b' de numéro hiérarchique 2 (donc rangé dans la cellule de rang 2 du tableau), son fils gauche est 'd', son fils droit est 'e'. 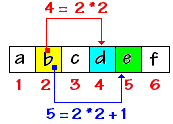
Arbre partiellement ordonné :
C'est un arbre étiqueté dont les valeurs des noeuds appartiennent à un ensemble muni d'une relation d'ordre total (les nombres entiers, réels etc... en sont des exemples) tel que pour un noeud donné tous ses fils ont une valeur supérieure ou égale à celle de leur père. Exemple de deux arbres partiellement ordonnés sur l'ensemble {20,27,29,30,32,38,45,45,50,51,67,85} d'entiers naturels :
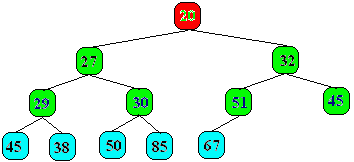
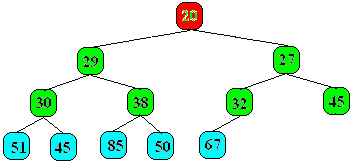
Nous remarquons que la racine d'un tel arbre est toujours l'élément de l'ensemble possédant la valeur minimum (le plus petit élément de l'ensemble), car la valeur de ce noeud par construction est inférieure à celle de ses fils et par transitivité de la relation d'ordre à celles de ses descendants c'est le minimum. Si donc nous arrivons à ranger une liste d'éléments dans un tel arbre le minimum de cette liste est atteignable immédiatement comme racine de l'arbre.
En reprenant l'exemple précédent sur 3 niveaux : (entre parenthèses le numéro hiérarchique du noeud)
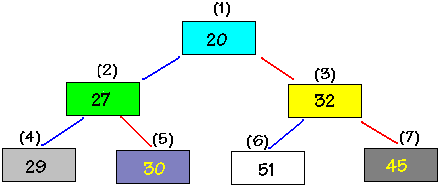
Voici réellement ce qui est stocké dans le tableau :(entre parenthèses l'index de la cellule contenant le noeud)
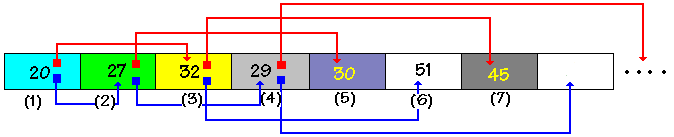
Le tas :
On appelle tas un tableau représentant un arbre parfait partiellement ordonné.L'intérêt d'utiliser un arbre parfait complet ou incomplet réside dans le fait que le tableau est toujours compacté, les cellules vides s'il y en a se situent à la fin du tableau.
Le fait d'être partiellement ordonné sur les valeurs permet d'avoir immédiatement un extremum à la racine.
2.5 Parcours d'un arbre binaire
Objectif : les arbres sont des structures de données. Les informations sont contenues dans les noeuds de l'arbre, afin de construire des algorithmes effectuant des opérations sur ces informations (ajout, suppression, modification,...) il nous faut pouvoir examiner tous les noeuds d'un arbre. Nous devons avoir à notre disposition un moyen de parcourir ou traverser chaque noeud de l'arbre et d'appliquer un traitement à la donnée rattachée à chaque noeud.
L'opération qui consiste à retrouver systématiquement tous les noeuds d'un arbre et d'y appliquer un même traitement se dénomme parcours de l'arbre. Parcours en largeur ou hiérarchique :
Un algorithme classique consiste à explorer chaque noeud d'un niveau donné de gauche à droite, puis de passer au niveau suivant. On dénomme cette stratégie le parcours en largeur de l'arbre. Exemple (déjà cité ci-haut) :

Algorithme de parcours en largeur (hiérarchique)
Cet algorithme nécessite l'utilisation d'un file du type Fifo dans laquelle l'on stocke les noeuds. Largeur ( Arbre )
si Arbre ¹ Æ alors
ajouter racine de l'Arbre dans Fifo;
tantque Fifo ¹ Æ faire
prendre premier de Fifo;
traiter premier de Fifo;
ajouter filsG de premier de Fifo dans Fifo;
ajouter filsD de premier de Fifo dans Fifo;
ftant
FsiUn autre algorithme général de parcours d'un arbre est employé très souvent, il s'agit du parcours dit "en profondeur".
Parcours en profondeur :
La stratégie consiste à descendre le plus profondément soit jusqu'aux feuilles d'un noeud de l'arbre, puis lorsque toutes les feuilles du noeud ont été visitées, l'algorithme "remonte" au noeud plus haut dont les feuilles n'ont pas encore été visitées. Notons que ce parcours peut s'effectuer systématiquement en commençant par le fils gauche, puis en examinant le fils droit ou bien l'inverse.
Parcours en profondeur par la gauche :
Traditionnellement c'est l'exploration fils gauche, puis ensuite fils droit qui est retenue on dit alors que l'on traverse l'arbre en "profondeur par la gauche". Schémas montrant le principe du parcours exhaustif en "profondeur par la gauche" :
Soit l'arbre binaire suivant:
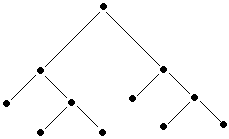
Appliquons lui la méthode de parcours proposée :
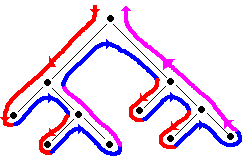
Chaque noeud a bien été examiné selon les principes du parcours en profondeur :
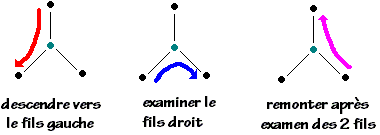
En fait pour ne pas surcharger les schémas arborescents, nous omettons de dessiner à la fin de chaque noeud de type feuille les deux noeuds enfants vides qui permettent de reconnaître que le parent est une feuille :
Lorsque la compréhension nécessitera leur dessin nous conseillons au lecteur de faire figurer explicitement dans son schéma arborescent les noeuds vides au bout de chaque feuille.
Algorithme général récursif de parcours en profondeur :
si Arbre ¹ Æ alors
Traiter-1 (info(Arbre.Racine)) ;
parcourir ( Arbre.filsG ) ;
Traiter-2 (info(Arbre.Racine)) ;
parcourir ( Arbre.filsD ) ;
Traiter-3 (info(Arbre.Racine)) ;
Fsi
Les différents traitements Traiter-1 ,Traiter-2 et Traiter-3 consistent à traiter l'information située dans le noeud actuellement traversé soit lorsque l'on descend vers le fils gauche ( Traiter-1 ), soit en allant examiner le fils droit ( Traiter-2 ), soit lors de la remonté après examen des 2 fils ( Traiter-3 ).
En fait on n'utilise que trois variantes de cet algorithme, celles qui constituent des parcours ordonnés de l'arbre en fonction de l'application du traitement de l'information située aux noeuds. Chacun de ces 3 parcours définissent un ordre implicite (préfixé, infixé, postfixé) sur l'affichage et le traitement des données contenues dans l'arbre.Algorithme de parcours en pré-ordre : (ordre préfixé)
parcourir ( Arbre )
si Arbre ¹Æ alors
Traiter-1 (info(Arbre.Racine)) ;
parcourir ( Arbre.filsG ) ;
parcourir ( Arbre.filsD ) ;
Fsi
Algorithme de parcours en post-ordre : (ordre postfixé)
parcourir ( Arbre )
si Arbre ¹Æ alors
parcourir ( Arbre.filsG ) ;
parcourir ( Arbre.filsD ) ;
Traiter-3 (info(Arbre.Racine)) ;
Fsi
Algorithme de parcours en ordre symétrique : (ordre infixé)
parcourir ( Arbre )
si Arbre ¹Æ alors
parcourir ( Arbre.filsG) ;
Traiter-2 (info(Arbre.Racine)) ;
parcourir ( Arbre.filsD ) ;
Fsi
Illustration pratique d'un parcours général en profondeurLe lecteur trouvera ailleurs des exemples de parcours selon l'un des 3 ordres infixé, préfixé, postfixé, nous proposons un exemple didactique de parcours général avec les 3 traitements.
L'assistant d'algorithmes propose des exemples d'arbres de programmation d'algorithmes simples, en particulier celui de l'équation du second degré. Nous allons voir comment utiliser une telle structure arborescente afin de restituer du texte algorithmique linéaire.
Voici ce que nous donne l'assistant :
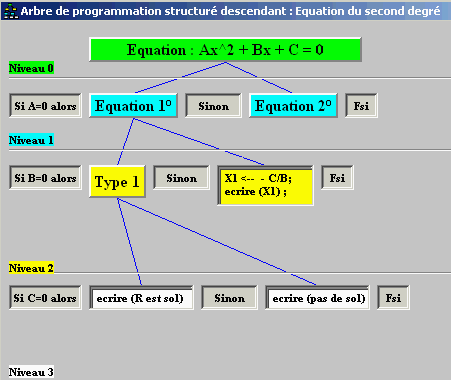
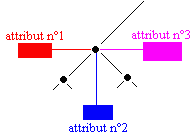
Nous pouvons établir un modèle d'arbre (binaire ici) où les informations au noeud sont au nombre de 3 (nous les nommerons attribut n°1, attribut n°2 et attribut n°3). Chaque attribut est une chaîne de caractères, vide s'il y a lieu.
Nous noterons ainsi un attribut contenant une chaîne vide :
Æ Ci-dessous une représentation de l'arbre de programmation précédent :
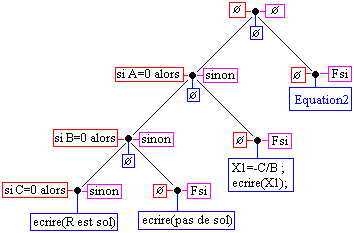
Traitement des attributs pour produire le texte :
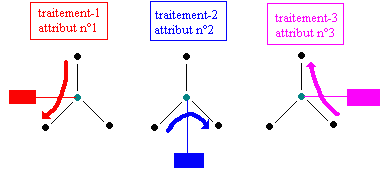
Traiter-1 (Arbre.Racine.Attribut n°1) consiste à écrire le contenu de l'Attribut n°1 :
si Attribut n°1 non vide alors
ecrire( Attribut n°1 )
Fsi
Traiter-2 (Arbre.Racine.Attribut n°2) consiste à écrire le contenu de l'Attribut n°2 :
si Attribut n°2 non vide alors
ecrire( Attribut n°2 )
Fsi
Traiter-3 (Arbre.Racine.Attribut n°3) consiste à écrire le contenu de l'Attribut n°3 :
si Attribut n°3 non vide alors
ecrire( Attribut n°3 )
Fsi
Parcours en profondeur de l'arbre de programmation de l'équation du second degré :
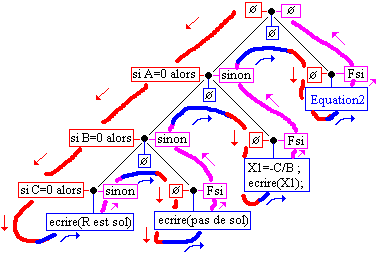
si Arbre ¹ Æ alors
Traiter-1 (Attribut n°1) ;
parcourir ( Arbre.filsG ) ;
Traiter-2 (Attribut n°2) ;
parcourir ( Arbre.filsD ) ;
Traiter-3 (Attribut n°3) ;
FsiTexte produit après parcours :
Æ
si A=0 alors
si B=0 alors
si C=0 alors
ecrire(R est sol)
sinon
Æ
Æ
ecrire(pas de sol)
Fsi
sinon
Æ
Æ
X1=-C/B;
ecrire(X1);
Fsi
sinon
Æ
Æ
Equation2
Fsi
ÆRappellons que le symbole Æ représente la chaîne vide il est uniquement mis dans le texe dans le but de permettre le suivi du parcours de l'arbre.
Pour bien comprendre le parcours aux feuilles de l'arbre précédent, nous avons fait figurer ci-dessous sur un exemple, les noeuds vides de chaque feuille et le parcours complet associé :
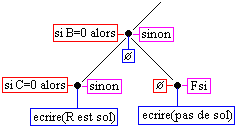
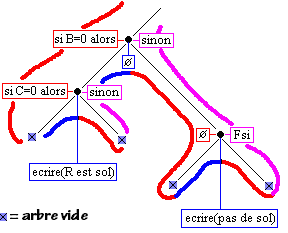
Le parcours partiel ci-haut produit le texte algorithmique suivant (le symbole Æ est encore écrit pour la compréhension de la traversée) :
si B=0 alors
si C=0 alors
ecrire(R est sol)
sinon
Æ
Æ
ecrire(pas de sol)
Fsi
sinon
Exercice proposé au lecteurSoit l'arbre suivant possédant 2 attributs par noeuds (un symbole de type caractère)
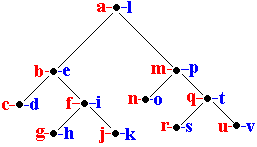
On propose le traitement en profondeur de l'arbre comme suit :
L'attribut de gauche est écrit en descendant, l'attribut de droite est écrit en remontant, il n'y a pas d'attribut ni de traitement lors de l'examen du fils droit en venant du fils gauche.écrire la chaîne de caractère obtenue par le parcours ainsi défini.
Réponse : abcdfghjkiemnoqrsuv
Terminons cette revue des descriptions algorithmiques des différents parcours classiques d'arbre binaire avec le parcours en largeur (Cet algorithme nécessite l'utilisation d'un file du type Fifo dans laquelle l'on stocke les nœuds).
Algorithme de parcours en largeur
si Arbre ¹Æ alors
ajouter racine de l'Arbre dans Fifo;
tantque Fifo ¹Æ faire
prendre premier de Fifo;
traiter premier de Fifo;
ajouter filsG de premier de Fifo dans Fifo;
ajouter filsD de premier de Fifo dans Fifo;
ftant
Fsi