C'est un tri également appelé tri par tas (heapsort,
en anglais). Il utilise une structure de données temporaire dénommée
"tas" comme mémoire de travail. C'est une variante
de méthode de tri par sélection où l'on parcourt le
tableau des éléments en sélectionnant et conservant les
minimas successifs (plus petits éléments partiels) dans un
arbre parfait partiellement ordonné.
| Définitions préliminaires d'arbres parfaits, partiellement ordonnés et tas |
Définition - 1 / Arbre parfait :
| c'est un arbre binaire dont tous les noeuds de chaque niveau sont présents sauf éventuellement au dernier niveau où il peut manquer des noeuds (noeuds terminaux = feuilles), dans ce cas l'arbre parfait est un arbre binaire incomplet et les feuilles du dernier niveau doivent être regroupées à partir de la gauche de l'arbre. |
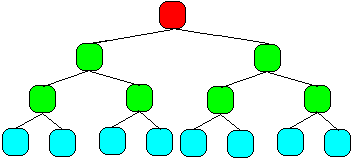
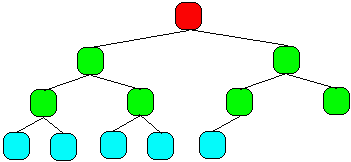
un arbre parfait complet
|
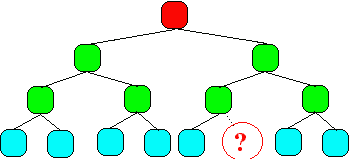
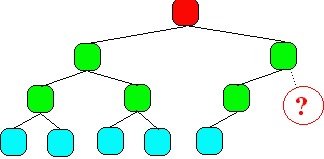
un arbre non parfait
|
Définition - 2 / Arbre partiellement ordonné :
| C'est un arbre étiqueté dont les noeuds appartiennent à un ensemble muni d'une relation d'ordre total (les nombres entiers, réels etc... en sont des exemples) tel que pour un noeud donné tous ses fils ont une valeur supérieure ou égale à celle de leur père. |
Exemple de deux arbres partiellement ordonnés sur l'ensemble {20,27,29,30,32,38,45,45,50,51,67,85} d'entiers naturels :
|
|
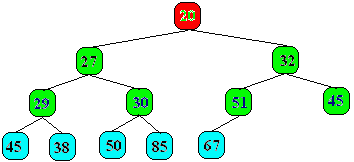
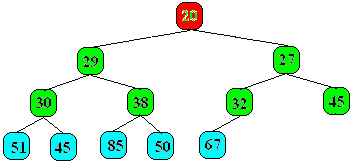
Nous remarquons que la racine d'un tel arbre
est toujours l'élément de l'ensemble possédant la valeur
minimum (le plus petit élément de l'ensemble), car
la valeur de ce noeud par construction est inférieure à celle
de ses fils et par transitivité de la relation d'ordre à celles
de ses descendants c'est le minimum. Si donc nous arrivons à ranger
une liste d'éléments dans un tel arbre le minimum de cette
liste est atteignable immédiatement comme racine de l'arbre.
Définition - 3 / Le tas :
| On appelle tas un tableau représentant un arbre parfait partiellement ordonné. |
| Principe du tri par tas |
Soit une liste (a1, a2, ... , an) d'éléments
appartenant à un ensemble totalementordonné (entiers, chaînes
de caractères,...) le principe est de parcourir
la liste (a1, a2, ... , an) en ajoutant chaque élément
ak dans un arbre parfait partiellement ordonné.
- L'insertion d'un nouvel élément ak dans l'arbre a lieu dans la dernière feuille vide de l'arbre à partir de la gauche (ou bien si le niveau est complet en recommençant un nouveau niveau par sa feuille la plus à gauche) et, en effectuant des échanges tant que la valeur de ak est inférieur à celle de son pére. Lorsque tous les éléments de la liste seront placés dans l'arbre, l'élément minimum "ai" de la liste (a1, a2, ... , an) se retrouve à la racine de l'arbre qui est alors partiellement ordonné.
- On recommence le travail sur la nouvelle liste (a1, a2, ... , an)-{ai}(la précédente privée de son minimum), pour cela on supprime l'élément minimum ai de l'arbre pour le mettre dans la liste triée puis, on prend l'élément de la dernière feuille du dernier niveau et on le place à la racine. On effectue ensuite des échanges de contenu avec le fils dont le contenu est inférieur, en partant de la racine, et en descendant vers le fils avec lequel on a fait un échange, ceci tant qu'il n'a pas un contenu inférieur à ceux de ses deux fils (ou de son seul fils) ou tant qu'il n'est pas à une feuille.
- On recommence l'opération de suppression et d'échanges éventuels jusqu'à ce que l'arbre ne contienne plus aucun élément.
La suite (a1, a2, ... , an) est rangée dans un tableau T[...] correspondant au tableau d'initialisation. Puis les éléments de ce tableau sont ajouter et traiter un par un dans un arbre avant d'être ajoutés dans un tableau trié en ordre décroissant ou croissant, selon le choix de l'utilisateur.
Rappelons qu'un arbre binaire parfait se représente classiquement par un tableau :
Si t est ce tableau, on a les règles suivantes :
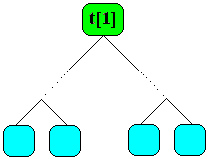
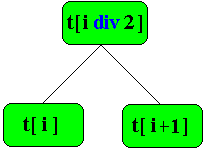
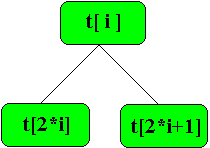
si i est supérieur à p div 2, t[i] est une feuille. |
| B-1 ) Figures illustrant le placement des éléments de la liste dans l'arbre : |
Exemple d'initialisation sur un tableau à 15 éléments :
Insertion du premier élément (le nombre 7) à la
racine de l'arbre :
Insertion du second élément (le nombre 27, 27 > 7
donc c'est un fils du noeud 7) :
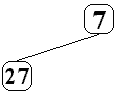
Insertion du troisième élément (le nombre 41,
41 > 7 c'est un fils du noeud 7) :
Insertion du quatrième élément (le nombre 30,
comme le niveau des fils du noeud 7 est complet, 30 est placé automatiquement
sur une nouvelle feuille d'un nouveau niveau, puis il est comparé à
son père 27, 30 > 27 c'est donc un fils du noeud 27 il n'y a pas
d'échange ) :
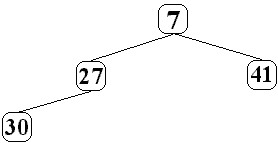
Insertion du cinquième élément (le nombre 10) : L'insertion
du nouvel élément 10 dans l'arbre a lieu automatiquement dans
la dernière feuille vide de l'arbre à partir de la gauche, ici
le fils droit de 27 :
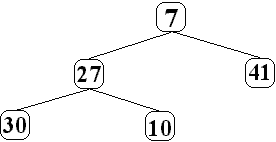
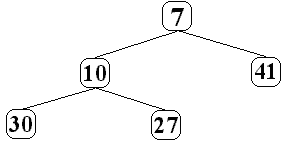
Le processus continue avec l'élément suivant de la liste
le nombre 31:
31 est automatiquement rangé sur la première feuille disponible
à gauche soit le fils gauche de 41:
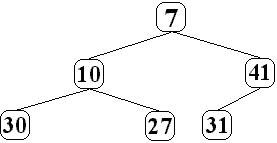
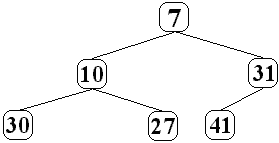etc....
Observons maintenant comment l'élément minimum de la liste qui est le onzième élément, soit le nombre 3, est rangé dans l'arbre.
Voici l'état de l'arbre avant introduction du nombre 3 :
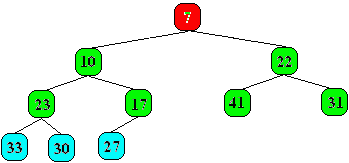
Le nombre 3 est introduit sur la première feuille libre du niveau bleu
:
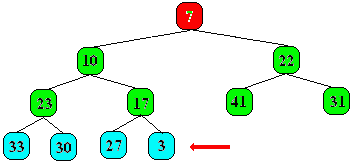
Il est comparé à son père le noeud 17, comme 3 <
17, il y a alors échange :
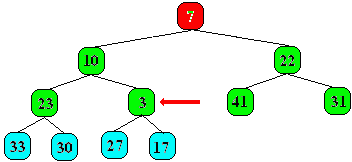
Il est ensuite comparé à son nouveau père le noeud
10, comme 3 < 10, il y a alors échange :
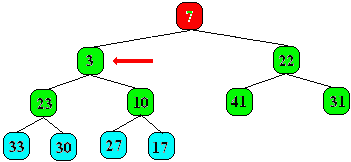
Il est enfin comparé à son dernier père (la racine
de l'arbre), comme 3 < 7, il y a alors échange :
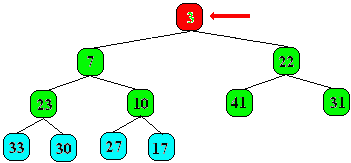
C'est l'élément 3 qui est maintenant la racine
de l'arbre, comme les 4 éléments suivants sont plus grand que
3, ils seront rangés plus bas dans l'arbre (cf. figure ci-dessous)
:
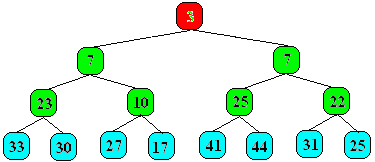
Conclusion sur le premier passage :
| La liste initiale :
est finalement stockée ainsi : |
| B-2 ) Figures illustrant la suppression de la racine : |
Le nombre 3 est le plus petit élément, on le supprime
de l'arbre et l'on prend l'élément de
la dernière feuille du dernier niveau (ici le nombre 25) et on le
place à la racine (à la place qu'occupait le nombre 3)
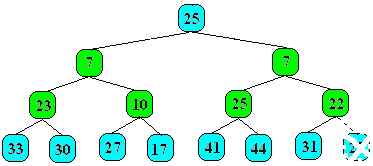
et l'on recommence les échanges éventuels
en comparant la racine avec ses descendants :
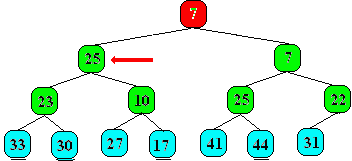le fils gauche 23 est inférieur à 25 => échange
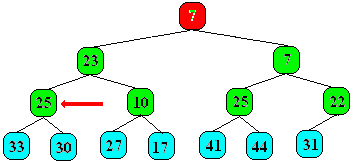Arrêt du processus (33 > 25 et 30 > 25)
On obtient le deuxième plus petit élément à la racine de l'arbre, ici le nombre 7.
On continue à "vider" ainsi l'arbre et déplaçant les feuilles vers la racine et en échangeant les noeuds mal placés. A la fin nous avons extrait à chaque étape le plus petit élément de chaque sous liste restante et nous obtenons les éléments de la liste classés par ordre (croissant ou décroissant selon notre choix).
Notre version de tri par tas comporte les étapes suivantes :
- initialisation : ajouter successivement chacun des n éléments dans le tas t[1..p]; p augmente de 1 après chaque adjonction . A la fin on a un tas de taille p = n.
- tant que p est plus grand que 1, supprimer le minimum du tas (p décroît de 1), réorganiser le tas, ranger le minimum obtenue à la (p + 1)ième place.
On en déduit l'algorithme ci-dessous composé de 2 sous
algorithmes Ajouter pour la première
étape, et Supprimer pour la seconde.
|
Cette version de l'algorithme construit le tas par n appels de la procédure Ajouter et effectue les sélections par n - 1 appels de la procédure Supprimer.
Le coût et de l'ordre de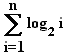 
comparaisons, au pire.
La complexité au pire en nombre de comparaisons est en
O(n log n).
Le nombre d'échanges dans le tas est majoré par le nombre de comparaisons et il est du même ordre de grandeur.
La complexité au pire en nombre de transferts du tri par tas
est donc en O(n log n).
| program TriParArbre; const Max =10; // nombre maximal d'éléments du tableau type TTab=array [1..Max] of integer; // TTab : Type Tableau var Tas, TabInit, TabTrie : TTab; // Tas, tableau initial puis tableau triéTableau P, Lemin : integer;
Initialisation(TabInit); writeln('TRI PAR ARBRE'); writeln; Impression(TabInit); P:=0; while p < Max do Ajouter ( Tas, p, TabInit[p+1] ); while p >= 1 do begin Supprimer ( Tas, P, Lemin ) ; TabTrie[Max-P]:=Lemin end; Impression(TabTrie); writeln('----------------------'); readln end. |
REMARQUE IMPORTANTE
Notons que dans la procédure nous avons traduit la condition de la boucle :
| Tantque (j
> 1) et (Tas[j] < Tas[j div 2]) faire temp ¬ Tas[j] ; Tas[j] ¬ Tas[j div 2] ; Tas[j div 2] ¬ temp ; j ¬ j div 2 ; finTant |
par les lignes de programmes suivantes :
| if j>1 then While Tas[j] < Tas[j div 2] do begin temp := Tas[j] ; Tas[j] := Tas[j div 2] ; Tas[j div 2] := temp ; j := j div 2 ; if j<=1 then break end |
ceci afin d'éviter un incident dû
à un effet de bord. Lorsque l'indice "j" prend par exemple la valeur
1, l'indice "j div 2" vaut alors 0 et cette valeur n'est pas
valide puisque l'indice de tableau varie entre 1..Max.
On peut pallier aussi d'une autre manière
à cet inconvenient en ajoutant une sentinelle "à gauche
dans le tableau" en étendant la borne inférieure à la
valeur 0,
les indices pouvant alors varier entre 0..Max. On obtient une
autre écriture de la procédure "Ajouter" suivant l'algorithme
de près :
| type TTab=array [0..Max]
of integer; // 0 est
l'indice sentinelle
procedure Ajouter (var Tas
: TTab; var P, x : integer); |
Résultat de l'exécution du programme précédent :
