Le tri par insertion
Assistants interactif animé : 
C'est un tri en général un peu plus coûteux en
particulier en nombre de transfert à effectuer qu'un tri par sélection
cf. complexité.
A) Spécification
abstraite
Son principe est de parcourir la liste non triée (a1,
a2, ... , an) en la décomposant en deux parties une partie
tdéjà triée et une partie non triée. La méthode
est identique à celle que l'on utilise pour ranger des cartes que l'on
tient dans sa main : on insère dans le paquet de cartes déjà
rangées une nouvelle carte au bon endroit. L'opération de base
consiste à prendre l'élément frontière dans la
partie non triée, puis à l'insérer à sa place
dans la partie triée (place que l'on recherchera séquentiellement),
puis à déplacer la frontière d'une position vers la droite.
Ces insertions s'effectuent tant qu'il reste un élément à
ranger dans la partie non triée.. L'insertion de l'élément
frontière est effectuée par décalages successifs d'une
cellule.
La liste (a1, a2, ... , an) est décomposée
en deux parties : une partie triée (a1, a2, ... , ak)
et une partie non-triée (ak+1, ak+2, ... , an);
l'élément ak+1 est appelé élément
frontière (c'est le premier élément non trié).
B) Spécification
concrète itérative
La suite (a1, a2, ... , an) est rangée dans
un tableau T[...] en mémoire centrale. Le tableau contient une partie
triée ((a1, a2, ... , ak) en violet à gauche)
et une partie non triée ((ak+1, ak+2, ... , an)
en blanc à droite).
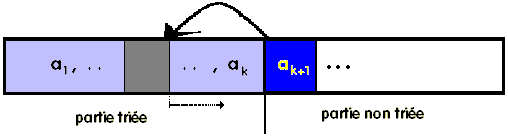
En faisant varier j de k jusqu'à 2 , afin de balayer toute la
partie (a1, a2, ... , ak) déjà rangée,
on décale d'une place les éléments plus grands que l'élément
frontière :
tantque aj-1 > ak+1 faire
décaler aj-1 en
aj ;
passer au j précédent
ftant
La boucle s'arrête lorsque aj-1 < ak+1,ce qui
veut dire que l'on vient de trouver au rang j-1 un élément aj-1
plus petit que l'élément frontière ak+1, donc
ak+1 doit être placé au rang j.
C) Algorithme
:
Algorithme Tri_Insertion
local: i , j , n,
v Î Entiers naturels
Entrée : Tab Î
Tableau d'Entiers naturels de 0 à n
éléments
Sortie : Tab Î
Tableau d'Entiers naturels de 0 à n
éléments
{ dans la cellule de rang 0 se trouve une sentinelle
chargée d'éviter de tester dans la boucle tantque .. faire
si l'indice j n'est pas inférieur
à 1, elle aura une valeur inférieure à toute valeur
possible de la liste
}
début
pour i de2 jusquà n faire// la partie non encore triée (ai, ai+1,
... , an)
v ¬ Tab[ i ] ;
// l'élément frontière
: ai
j ¬ i ;
// le rang de l'élément frontière
Tantque
Tab[ j-1 ] > v faire//on travaille sur la partie déjà triée
(a1, a2, ... , ai)
Tab[ j ] ¬ Tab[ j-1 ]; // on décale l'élément
j ¬ j-1;
// on passe au rang précédent
FinTant
;
Tab[ j ] ¬
v //on recopie ai dans la place libérée
fpour
Fin Tri_Insertion |
Sans la sentinelle en T[0] nous aurions une comparaison sur j à
l'intérieur de la boucle :
Tantque Tab[ j-1 ] > v faire//on travaille
sur la partie déjà triée (a1, a2, ...
, ai)
Tab[ j ] ¬ Tab[ j-1 ]; // on décale l'élément
j ¬ j-1;
// on passe au rang précédent
si j = 0 alorsSortir de la boucle fsi
FinTant ;
| Un étudiant a proposé
d'intégrer la comparaison dans le test de la boucle en écrivant
ceci :
Tantque ( Tab[j-1] > v ) et ( j >0 ) faire
Tab[ j ] ¬ Tab[ j-1 ];
j ¬ j-1;
FinTant ;
Il a eu des problèmes de dépassement d'indice de
tableau lors de l'implémentation de son programme, essayez d'analyser
l'origine du problème en notant que la présence d'une sentinelle
élimine le problème.
|
D) Complexité
:
| Choisissons comme opération élémentaire
la comparaison de deux cellules
du tableau. |
Dans le pire des cas le nombre de comparaisons "Tantque Tab[ j-1 ] > v faire" est une valeur qui ne dépend que
de la longueur i de la partie (a1, a2, ... , ai)
déjà rangée. Il y a donc au pire i comparaisons pour
chaque i variant de 2 à n :
La complexité au pire en nombre de comparaison est donc égale
à la somme des n termes suivants (i = 2, i = 3,.... i = n)
C = 2 + 3 + 4 +...+ n = n(n+1)/2 -1 comparaisons au maximum. (c'est
la somme des n premiers entiers moins 1).
La complexité au pire en nombre de comparaison est de de l'ordre
de n², que l'on écrit O(n²).
| Choisissons maintenant comme opération élémentaire
le transfert d'une cellule du tableau. |
Calculons par dénombrement du nombre de transferts dans le pire
des cas . Il y a autant de transferts dans la boucle "Tantque Tab[ j-1 ] > v faire" qu'il y a de comparaisons il faut
ajouter 2 transferts par boucle "pour
i de 2 jusquà
n faire",
soit au total dans le pire des cas :
C = n(n+1)/2 + 2(n-1) = (n² + 5n - 4)/2
La complexité au pire en nombre de transferts est de l'ordre
de n², que l'on écrit O(n²).
E) Programme pascal
:
program TriParInsertion;
const N = 10; { Limite supérieure
de tableau }
type TTab = array [0..N]of
integer; { TTab : Type Tableau }
var Tab : TTab ;
procedure TriInsertion (var Tab:TTab) ;
{ Implantation Pascal de l'algorithme
}
var i, j, v : integer;
begin
for i := 2 to N do
begin
v := Tab[ i ];
j := i ;
while Tab[ j-1 ] > v do
begin
Tab[
j ] := Tab[ j-1 ] ;
j := j - 1 ;
end;
Tab[ j ] := v ;
end
end; |
procedure Initialisation(var Tab:TTab) ;
{ Tirage aléatoire de N nombres
de 1 à 100 }
var i : integer; { i :
Indice de tableau de N colonnes }
begin
randomize;
for i := 1 to N do
Tab[i] := random(100);
Tab[0]:= -Maxint ; // la sentinelle est l'entier le plus petit du type integer
sur la machine
end; |
procedure Impression(Tab:TTab) ;
{ Affichage des N nombres dans les colonnes
}
var i : integer;
begin
writeln('------------------------');
for i:= 1 to N do write(Tab[i] : 3, ' | ');
writeln;
end; |
begin
Initialisation(Tab);
writeln('TRI PAR INSERTION');
writeln;
Impression(Tab);
TriInsertion(Tab);
Impression(Tab);
writeln('----------------------');
end. |
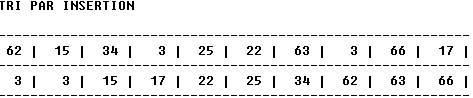
Résultat de l'exécution du programme précédent
:
F) Classe Java (tableau d'entiers)
class
ApplicationTriInsert
{
// le tableau è trier:
static
int
[] table
=
new
int
[10]
;
/*---------------------------------------------------------------------
Dans la cellule de rang 0 se trouve une sentinelle chargée d'éviter de tester dans la boucle tantque .. faire si
l'indice j n'est pas inférieur è 1, elle aura une valeur inférieure
à toute valeur possible de la liste
--------------------------------------------------------------------*/
static void
Impression
( )
{
// Affichage du tableau
int
n
=
table.length
-
1
;
for (
int
i
=
0
;
i
<=
n
;
i
++
)
System.out.print
(
table[i]
+
" , ");
System.out.println
();
}
static void
Initialisation
( )
{
// remplissage aléatoire du tableau
int
n
=
table.length
-
1
;
for (
int
i
=
1
;
i
<=
n
;
i
++
)
table[i]
=
(
int
)(
Math.random
()
*
100
);
//sentinelle à l'indice 0 :
table[0]
= -
Integer.MAX_VALUE
;
}
public static void
main
(
String
[ ] args
)
{
Initialisation
( );
System.out.println
("Tableau initial :");
Impression
( );
TriInsert
( );
System.out.println
("Tableau une fois trié :");
Impression
( );
}
static void
TriInsert
( )
{
// sous-programme de Tri par insertion :
int
n
=
table.length
-
1
;
for (
int
i
=
2
;
i
<=
n
;
i
++
)
{
int
v
=
table[i]
;
int
j
=
i
;
while (
table[ j
-
1 ]
>
v
)
{
// travail sur la partie déjè triée (a1, a2, ... , ai)
table[ j ]
=
table[ j
-
1 ]
;
// on décale l'élément
j
--
;
// on passe au rang précédent
}
table[ j ]
=
v
;
//on recopie ai dans la place libérée
}
}
}

