Le tri par sélection
deux versions

Assistants interactif animé : 
C'est une version volontairement inefficace de la catégorie
des tris par sélection,
l'amélioration est apportée dans un autre feuillet de cours.
A) Spécification
abstraite
La liste (a1, a2, ... , an) est décomposée
en deux parties : une partie triée (a1, a2, ... , ak)
et une partie non-triée (ak+1, ak+2, ... , an);
l'élément ak+1 est appelé élément
frontière (c'est le premier élément non trié).
Le principe est de parcourir la partie non-triée de la liste (ak+1,
ak+2, ... , an) en cherchant l'élément minimum,
puis en l'échangeant avec l'élément frontière
ak+1, puis à déplacer la frontière d'une
position. Il s'agit d'une récurrence sur les minima successifs. On
suppose que l'ordre s'écrit de gauche à droite (à gauche
le plus petit élément, à droite le plus grand élément).
On recommence l'opération avec la nouvelle sous-suite (ak+2,
... , an) , et ainsi de suite jusqu'à ce que la
dernière soit vide.
B) Spécification
concrète
La suite (a1, a2, ... , an) est rangée dans
un tableau T[...] en mémoire centrale. Le tableau contient une partie
triée (en violet à gauche) et une partie non triée (en
blanc à droite). On recopie le minimum de la partie non-triée
du tableau dans la cellule frontière (le premier élément
de cette partie).
si ak+1
> ap alors ak+1
<--- ap Fsi
et l'on obtient ainsi à la fin de l'examen de la sous-liste (ak+1,
ak+2, ... , an) la valeur min(ak+1, ak+2, ... ,
an) stockée dans la cellule ak+1. La sous-suite (a1,
a2, ... , ak, ak+1) est maintenant triée et l'on
recommence la boucle de rechercjhe du minimum sur la nouvelle sous-liste
(ak+2, ak+3, ... , an) etc...
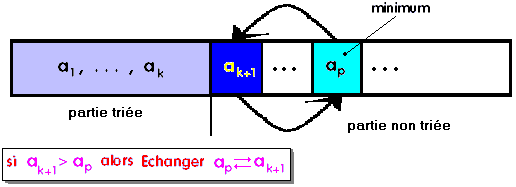
Tant que la partie non triée n'est pas vide,
on range le minimum de la partie non-triée dans l’élément
frontière.
C) Algorithme
:
Une version maladroite de l'algorithme mais exacte a
été fournie par un groupe d'étudiants elle est dénommée
/version 1/. Elle échange physiquement et systématiquement
l'élément frontière Tab[ i ] avec un élément
Tab[ j ] dont la valeur est plus petite (la suite (a1, a2, ...
, ai) est triée) :
Algorithme Tri_Selection /Version 1/
local: m, i , j , n, temp Î
Entiers naturels
Entrée : Tab Î
Tableau d'Entiers naturels de 1 à n éléments
Sortie : Tab Î
Tableau d'Entiers naturels de 1 à n éléments
début
pour i de 1 jusquà
n-1faire // recommence une sous-suite
m ¬ i
; // i est l'indice de l'élément frontière
Tab[ i ]
pour j de i+1 jusquà n faire// liste non-triée
: (ai+1, a2, ... , an)
si Tab[ j ] <
Tab[ m ] alors // aj est le nouveau minimum partiel
m ¬
j ;
temp ¬ Tab[ m ]
;
Tab[ m ] ¬ Tab[
i ] ;
Tab[ i ] ¬
temp //on échange les positions de
ai et de aj
m ¬ i ;
Fsi
fpour
fpour
Fin Tri_Selection
|
Voici une version correcte et améliorée
du précédent (nous allons voir avec la notion de complexité
comment appuyer cette intuition d'amélioration), dans laquelle l'on
sort l'échange ai et aj
de la boucle interne "pour j de
i+1 jusquà n
faire" pour le déporter
à la fin de cette boucle.
D) Complexité
:
| Choisissons comme opération élémentaire
la comparaison de deux cellules
du tableau. |
Pour les deux versions 1 et 2 :
Le nombre de comparaisons "si Tab[
j ] < Tab[ m ] alors" est une
valeur qui ne dépend que de la longueur n
de la liste (n est le nombre d'éléments
du tableau), ce nombre est égal au nombre de fois que les itérations
s'exécutent, le comptage montre que la boucle "pour i de
1 jusquà n-1 faire"
s'exécute n-1 fois (donc une somme de n-1 termes) et qu'à chaque
fois la boucle "pour j de i+1
jusquà n faire" exécute (n-(i+1)+1 fois la comparaison
"si Tab[ j ] < Tab[ m ] alors".
La complexité en nombre de comparaison est égale à
la somme des n-1 termes suivants (i = 1, ...i = n-1)
C = (n-2)+1 + (n-3)+1 +.....+1+0 = (n-1)+(n-2)+...+1 = n.(n-1)/2 (c'est
la somme des n-1 premiers entiers).
La complexité en nombre de comparaison est de de l'ordre de n²,
que l'on écrit O(n²).
| Choisissons maintenant comme opération élémentaire
l'échange de deux cellules
du tableau. |
Calculons par dénombrement du nombre d'échanges dans le pire
des cas (complexité au pire = majorant du nombre d'échanges).
Le cas le plus mauvais est celui où le tableau est déjà
classé mais dans l'ordre inverse.
Pour la version 1
| Au pire chaque cellule doit être échangée, dans
cette éventualité il y a donc autant d'échanges que de
tests.
La complexité au pire en nombre d'échanges de la
version 1 est de l'ordre de n², que l'on écrit O(n²).
|
Pour la version 2
| L'échange a lieu systématiquement dans la boucle principale
"pour i de 1 jusquà n-1 faire" qui s'exécute n-1 fois :
La complexité en nombre d'échanges de cellules
de la version 2 est de l'ordre de n, que l'on écrit O(n).
Un échange valant 3 transferts (affectation) la complexité
en transfert est O(3n) = O(n)
|
Toutefois cette complexité en nombre d'échanges de cellules
n'apparaît pas comme significative du tri, outre le nombre de comparaison,
c'est le nombre d'affectations d'indice qui représente une opération
fondamentale et là les deux versions ont exactement la même
complexité O(n²).
Exemple : soit la liste à 6 éléments ( 5 , 4 ,
2 , 3 , 7 ,1 ), appliquons la version 2 du tri par sélection
sur cette liste d'entiers. Visualisons les différents états
de la liste pour la première itération externe contrôlée
par i (i = 1) et pour les itérations internes contôlées
par l'indice j (de j = 2 ... à ... j = 6) :
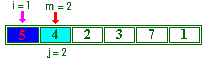
comme 5>4 on mémorise dans m |
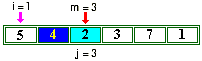
comme 4>2 on mémorise dans m |
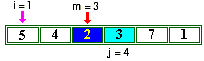
comme 2<3 on ne mémorise pas |
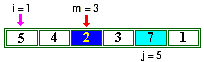
comme 2<7 on ne mémorise pas |

comme 2>1 on mémorise dans m |

on échange T[1] et T[6] |
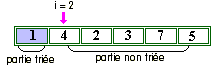
L'algorithme ayant terminé l'échange de T[1] et de T[6],
il passe à l'itération externe suivante ( i = 2) :
 etc....
etc....
E) Programme pascal
/Version 2/ :
program TriParSelection;
const N = 10; { Limite supérieure
de tableau }
type TTab = array [1..N] of integer; { TTab : Type Tableau }
var Tab : TTab ;
procedure TriSelection (var Tab:TTab) ;
{ Implantation Pascal de l'algorithme
}
var i, j, t, m : integer;
begin
for i := 1 to N-1 do
begin
m := i;
for j := i+1 to N do
if Tab[ j ] < Tab[
m ] then m := j;
t := Tab[m];
Tab[m] := Tab[i];
Tab[i] := t;
end;
end; |
procedure Initialisation(var Tab:TTab) ;
{ Tirage aléatoire de N nombres
de 1 à 100 }
var i : integer; { i
: Indice de tableau de N colonnes }
begin
randomize;
for i := 1 to N do
Tab[i] := random(100);
end; |
procedure Impression(Tab:TTab) ;
{ Affichage des N nombres dans les
colonnes }
var i : integer;
begin
writeln('------------------------');
for i:= 1 to N do write(Tab[i] : 3, ' | ');
writeln;
end; |
begin
Initialisation(Tab);
writeln('TRI PAR SELECTION');
writeln;
Impression(Tab);
TriSelection(Tab);
Impression(Tab);
writeln('----------------------');
end. |
Résultat de l'exécution du programme précédent
:

F) Classe Java (tableau d'entiers)
class
ApplicationTriSelect
{
static
int
[] table
=
new
int
[20]
;
// le tableau è trier en attribut
static void
Impression
( )
{
// Affichage du tableau
int
n
=
table.length
-
1
;
for (
int
i
=
1
;
i
<=
n
;
i
++
)
System.out.print
(
table[i]
+
" , ");
System.out.println
();
}
static void
Initialisation
( )
{
// remplissage aléatoire du tableau
int
n
=
table.length
-
1
;
for (
int
i
=
1
;
i
<=
n
;
i
++
)
table[i]
=
(
int
)(
Math.random
()
*
100
);
}
static void
TriSelect
( )
{
int
n
=
table.length
-
1
;
for (
int
i
=
1
;
i
<=
n
-
1
;
i
++
)
{
// recommence une sous-suite
int
m
=
i
;
// élément frontière ai = table[ i ]
for (
int
j
=
i
+
1
;
j
<=
n
;
j
++
)
// (ai+1, a2, ... , an)
if (
table[ j ]
<
table[ m ]
)
// aj = nouveau minimum partiel
m
=
j
;
// indice mémorisé
int
temp
=
table[ m ]
;
table[ m ]
=
table[ i ]
;
table[ i ]
=
temp
;
}
}
public static void
main
(
String
[ ] args
)
{
Initialisation
( );
System.out.println
("Tableau initial :");
Impression
( );
TriSelect
( );
System.out.println
("Tableau une fois trié :");
Impression
( );
}
}

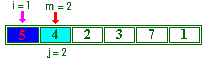


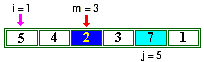


 etc....
etc.... 