méthode Sedgewick
- A) Spécification abstraite
- B) Spécification concrète
- C) Algorithme
- D) Complexité
- E) Procédure pascal
- F) Classe Java
C'est le plus performant des tris en table qui est certainement celui
qui est le plus employé dans les programmes. Ce tri a été
trouvé par C.A.Hoare, nous nous référons à
Robert Sedgewick qui a travaillé dans les
années 70 sur ce tri et l'a amélioré et nous renvoyons
à son ouvrage pour une étude complète de ce tri. Nous
donnons les principes de ce tri et sa complexité en moyenne et au
pire.
Son principe est de parcourir la liste L = (a1, a2, ... , an) en la divisant systématiquement en deux sous-listes L1 et L2. L'une est telle que tous ses éléments sont inférieurs à tous ceux de l'autre liste et en travaillant séparément sur chacune des deux sous-listes en réappliquant la même division à chacune des deux sous-listes jusqu'à obtenir uniquement des sous-listes à un seul élément.
C'est un algorithme dichotomique qui divise donc le problème en deux sous-problèmes dont les résultats sont réutilisés par recombinaison, il est donc de complexité O(n.log(n)).
Pour partitionner une liste L en deux sous-listes L1 et L2 :
- on choisit une valeur quelconque dans la liste L (la dernière par exemple) que l'on dénomme pivot,
- puis on construit la sous-liste L1 comme comprenant tous les éléments de L dont la valeur est inférieure ou égale au pivot,
- et l'on construit la sous-liste L2 comme constituée de tous les éléments dont la valeur est supérieure au pivot.
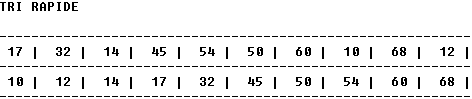
L = [ 4, 23, 3, 42, 2, 14, 45, 18, 38, 16 ]
prenons comme pivot la dernière valeur pivot = 16
Nous obtenons par exemple :
L1 = [4, 14, 3, 2]
L2 = [23, 45, 18, 38, 42]
A cette étape voici l'arrangement de
L :
L = L1 + pivot + L2 = [4, 14, 3, 2,
16,
23,
45, 18, 38, 42]
En effet, en travaillant sur la table elle-même par réarrangement
des valeurs, le pivot 16 est
placé au bon endroit directement :
[4<16, 14<16, 3<16, 2<16,
16,
23>16,
45>16, 18>16, 38>16, 42>16]
En appliquant la même démarche au deux sous-listes : L1
(pivot=2) et L2 (pivot=42)
[4, 14, 3, 2, 16,
23,
45, 18, 38, 42] nous obtenons :
L11=[ ] liste vide
L12=[3, 4, 14]
L1=L11 + pivot + L12 = (2,3,
4, 14)
L21=[23, 38, 18]
L22=[45]
L2=L21 + pivot + L22 = (23, 38, 18, 42,
45)
A cette étape voici le nouvel arrangement
de L :
L = [(2,3,
4, 14),
16,
(23, 38, 18, 42,
45)]
etc...
Ainsi de proche en proche en subdivisant le problème en deux
sous-problèmes, à chaque étape nous obtenons un pivot
bien placé.
La suite (a1, a2, ... , an) est rangée dans
un tableau T[...] en mémoire centrale.
Le processus de partionnement décrit ci-haut (appelé
aussi segmentation) est le point central du tri rapide, nous contruisons
une fonction Partition réalisant cette action .Comme l'on
ré-applique la même action sur les deux sous-listes obtenues
après partion, la méthode est donc récursive, le tri
rapide est alors une procédure récursive.
B-1 ) Voici une spécification générale de la
procédure de tri rapide :
Tri Rapide sur [a..b]
Tri Rapide sur [pivot'' .. y] Tri Rapide sur [x .. pivot'] |
B-2) Voici une spécification générale de la
fonction de partionnement :
La fonction de partionnement d'une liste [a..b] doit
répondre aux deux conditions suivantes :
[x .. pivot'] = T[G] , .. , T[i-1] ( où : x = T[G] et pivot' = T[i-1] ) tels que les T[G] , .. , T[i-1] sont tous inférieurs à T[i] , [pivot'' .. y] = T[i+1] , .. , T[D] ( où : y = T[D] et pivot'' = T[i+1] ) tels que les T[i+1] , .. , T[D] sont tous supérieurs à T[i] , |
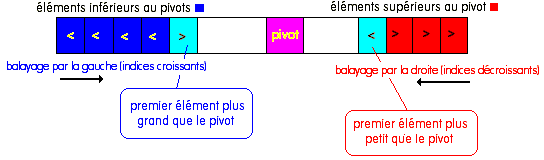
1) Dans le balayage par la gauche, on ne touche pas à un élément si sa valeur est inférieure au pivot (les éléments sont considérés comme étant alors dans la bonne sous-liste) on arrête ce balayage dès que l'on trouve un élément dont la valeur est plus grande que celle du pivot. Dans ce dernier cas cet élément n'est pas à sa place dans cette sous-liste mais plutôt dans l'autre sous-liste.
2) Dans le balayage par la droite, on ne touche pas à
un élément si sa valeur est supérieure au pivot
(les éléments sont considérés comme étant
alors dans la bonne sous-liste) on arrête ce balayage dès
que l'on trouve un élément dont la valeur est plus petite
que celle du pivot. Dans ce dernier cas cet élément n'est
pas à sa place dans cette sous-liste mais plutôt dans l'autre
sous-liste.
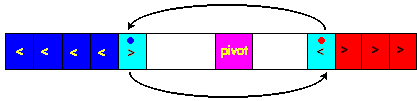
3) on procède à l'échange des deux éléments
mal placés dans chacune des sous-listes :
![]()
4) On continue le bayage par la gauche et le balayage par la droite tant que les éléments sont bien placés (valeur inférieure par la gauche et valeur supérieure par la droite), en échangeant à chaque fois les éléments mal placés.
5) La construction des deux sous-listes est terminée dès que l'on atteint (ou dépasse) le pivot.

Appliquons cette démarche à l'exemple précédent
: L = [ 4, 23, 3, 42, 2, 14, 45, 18, 38, 16 ]
4 < 16 => il est dans la bonne sous-liste, on continue
- liste en cours de construction : [ 4,16
]
- liste en cours de construction :[ 4,23,
16
]
38 > 16 => il est dans la bonne sous-liste, on continue
- liste en cours de construction : [ 4,23,
16,
38
]
- liste en cours de construction : [ 4,23,
16,
18,
38
]
- liste en cours de construction : [ 4,23,
16,
45,
18,
38
]
- liste en cours de construction : [ 4,23,
16,
14,
45,
18,
38
]
[ 4, 23, 16, 14, 45, 18, 38 ] ----> [ 4,14, 16, 23, 45, 18, 38 ]
--------¯----------------------------
[ 4, 14, 3, 42, 2, 23, 45, 18, 38, 16 ]
3 < 16 => il est dans la bonne sous-liste, on continue
- liste en cours de construction : [ 4,14,
3
,16,
23,
45,
18,
38
]
- liste en cours de construction : [ 4,14,
3,
42,
16,
23,
45,
18,
38
]
---------------¯---------------------
[ 4, 14, 3, 42, 2, 23, 45, 18, 38, 16 ]
- liste en cours de construction : [ 4,14,
3,
42,
16,
2,
23,
45,
18,
38
]
[ 4, 14, 3, 2, 16, 42, 23, 45, 18, 38 ]
et l'on arrête la construction puisque nous sommes arrivés
au pivot la fonction partition a terminé son travail elle a évalué
:
| - le pivot : 16
- la sous-liste de gauche : L1 = [4, 14, 3, 2] - la sous-liste de droite : L2 = [23, 45, 18, 38, 42] - la liste réarrangée : [ 4,14, 3, 2, 16, 42, 23, 45, 18, 38 ] |
Il reste à recommencer les mêmes opérations sur
les parties L1 et L2 jusqu'à ce que les partitions ne contiennent
plus qu'un seul élément.
Global :Tab[min..max] tableau d'entier
|
Nous supposons avoir mis une sentinelle dans le tableau, dans la première cellule la plus à gauche, avec une valeur plus petite que n'importe qu'elle autre valeur du tableau.
Cette sentinelle est utile lorsque le pivot choisi aléatoirement
se trouve être le plus petit élément de la table /pivot
= min (a1, a2, ... ,
an)/ :
| Comme nous avons:
"j , Tab[j] > piv , alors la boucle :
|
La sentinelle étant plus petite que tous les éléments
y compris le pivot arrêtera la boucle et encore une fois évite
de programmer le cas particulier du pivot = min (a1, a2,
... ,
an).