Traduction en Java
Recherche linéaire dans une table

TABLEAU NON TRIE

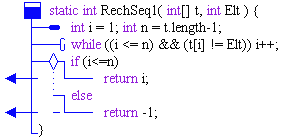
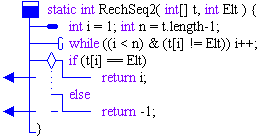
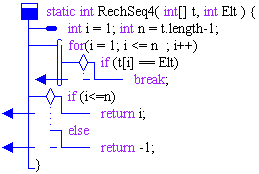
Une classe Java solution du problème :
 

Les différents sous-programmes Java implantant les 4 versions d'algorithme de recherche linéaire (table non triée) :
 

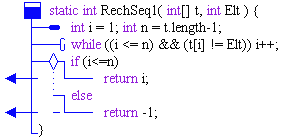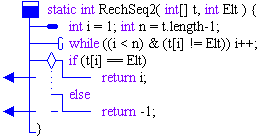Une classe complète permettant l'exécution des sous-programmes précédents :

 
    import Readln;
    class ApplicationRechLin  {

      static int max = 20;
      static int[] table = new int[max] ; //20 cellules à examiner de 1 à 19
      static int[] tableSent = new int[max+1] ; // le tableau à examiner de 1 à 20


       static void AfficherTable (int[] t ) {
           // Affichage du tableau 
         int n = t.length-1;
         for ( int i = 1; i <= n; i++) 
            System.out.print(t[i]+" , ");
         System.out.println();
      }

       static void InitTable  ( ) {
           // remplissage aléatoire du tableau 
         int n = table.length-1;
         for ( int i = 1; i <= n; i++) {
            table[i] = (int)(Math.random()*100);
            tableSent[i] = table[i];
         }
      }

       static int RechSeq1( int[] t, int Elt ) {
          int i = 1; int n = t.length-1;
         while ((i <= n) && (t[i] != Elt)) i++;
         if (i<=n) 
           return i;
         else 
            return -1;
      }

       static int RechSeq2( int[] t, int Elt ) {
         int i = 1; int n = t.length-1;
         while ((i < n) & (t[i] != Elt)) i++;
         if (t[i] == Elt) 
           return i;
         else 
            return -1;
      }

       static int RechSeq3( int[] t, int Elt ) {
         int i = 1; int n = t.length-2;
         t[n+1]= Elt ; //sentinelle
         while ((i <= n) & (t[i] != Elt)) i++;
         if (i<=n) 
           return i;
         else 
            return -1;
      }

       static int RechSeq4( int[] t, int Elt ) {
         int i = 1; int n = t.length-1;
         for(i = 1; i <= n  ; i++) 
           if (t[i] == Elt) 
               break;
         if (i<=n) 
           return i;
         else 
            return -1;
      }

       static void main(String[ ] args) {
         InitTable ( );
         System.out.println("Tableau initial :");
         AfficherTable (table );
         int x = Readln.unint(), rang;
         //rang = RechSeq1( table, x );
         //rang = RechSeq2( table, x );
         //rang = RechSeq3( tableSent, x );
         rang = RechSeq4( table, x );
         if (rang >0) 
            System.out.println("Elément "+x+" trouvé en : "+rang);
         else  System.out.println("Elément "+x+" non trouvé !");
      } 
   }
Source recopiable (cliquez sur le lien)
Image en diagrammes structurés JGrasp-Like du programme

informations sur les diagrammes
Remonter 

TABLEAU DEJA TRIE
 

Une classe Java solution du problème :

Les deux méthodesJava implantant les 2 versions d'algorithme de recherche linéaire (table triée) :


 

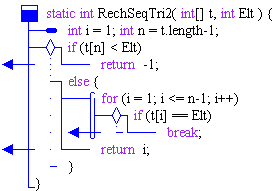
Une classe complète utilisant ces deux méthodes :
 
 import Readln;
    class ApplicationRechLinTrie  {

      static int[] table = new int[20] ; //20 cellules à examiner de 1 à 19


       static void AfficherTable (int[] t ) {
           // Affichage du tableau 
         int n = t.length-1;
         for ( int i = 1; i<=n; i++) 
            System.out.print(t[i]+" , ");
         System.out.println();
      }

       static void InitTable  ( ) {
            // remplissage aléatoire du tableau 
         int n = table.length-1;
         for ( int i = 1; i<=n; i++) {
            table[i] = (int)(Math.random()*100);
         }
      }

       static void TriInsert ( ) {
         // sous-programme de Tri par insertion :
         int n = table.length-1;
         for ( int i = 2; i <= n; i++) {
           int v = table[i];
           int j = i;
           while (table[ j-1 ] > v) {
               table[ j ] = table[ j-1 ]; 
               j = j-1; 
            } 
            table[ j ]  = v ; 
         }
      }

       static int RechSeqTri1( int[] t, int Elt ) {
         int i = 1; int n = t.length-1;
         if (t[n] < Elt) 
           return  -1;
         else {
           while (t[i] < Elt) i++;
           return  i ; 
         }
      }

       static int RechSeqTri2( int[] t, int Elt ) {
         int i = 1; int n = t.length-1;
         if (t[n] < Elt) 
           return  -1;
         else {
           for (i = 1; i <= n-1; i++) 
             if (t[i] == Elt) 
                break;
           return  i;
         }
      }

       static void main(String[ ] args) {
         InitTable ( );
         System.out.println("Tableau initial :");
         AfficherTable (table );
         TriInsert ( );
         System.out.println("Tableau trié :");
         AfficherTable (table );
         int x = Readln.unint(), rang;
         //rang = RechSeqTri1( table, x );
         rang = RechSeqTri2( table, x );
         if (rang >0) 
            System.out.println("Elément "+x+" trouvé en : "+rang);
         else  System.out.println("Elément "+x+" non trouvé !");
      } 
   }

Source recopiable (cliquez sur le lien)

Remonter