Objectif : Ecrire un programme Java implémentant l'algorithme du tri par arbre (ou tri en tas).

Rappels des spécifications du cours
Algorithme proposé
Implantation en Java
Squelette de classe Java à implanter
 

Spécifications de l’algorithme-Rappels du cours

Spécification abstraite

Soit une liste (a1, a2, ... , an) d'éléments appartenant à un ensemble totalementordonné (entiers, chaînes de caractères,...) le principe est de parcourir la liste (a1, a2, ... , an) en ajoutant chaque élément ak dans un arbre binaire parfait partiellement ordonné.
 

• L'insertion d'un nouvel élément ak dans l'arbre a lieu dans la dernière feuille vide de l'arbre à partir de la gauche (ou bien si le niveau est complet en recommençant un nouveau niveau par sa feuille la plus à gauche) et, en effectuant des échanges tant que la valeur de ak est inférieur à celle de son pére. Lorsque tous les éléments de la liste seront placés dans l'arbre, l'élément minimum "ai" de la liste (a1, a2, ... , an) se retrouve à la racine de l'arbre qui est alors partiellement ordonné.

• On recommence le travail sur la nouvelle liste (a1, a2, ... , an)-{ai}(la précédente privée de son minimum), pour cela on supprime l'élément minimum ai de l'arbre pour le mettre dans la liste triée puis, on prend l'élément de la dernière feuille du dernier niveau et on le place à la racine. On effectue ensuite des échanges de contenu avec le fils dont le contenu est inférieur, en partant de la racine, et en descendant vers le fils avec lequel on a fait un échange, ceci tant qu'il n'a pas un contenu inférieur à ceux de ses deux fils (ou de son seul fils) ou tant qu'il n'est pas à une feuille.

• On recommence l'opération de suppression et d'échanges éventuels jusqu'à ce que l'arbre ne contienne plus aucun élément.

Remonter 

Spécification concrète

Rappelons qu'un arbre binaire parfait se représente classiquement par un tableau :

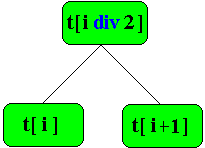
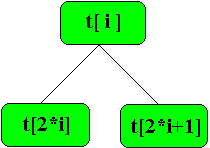
Si t est ce tableau, on a les règles suivantes : t[1] est la racine :   t[i div 2] est le père de t[i] pour i > 1 :   t[2 * i] et t[2 * i + 1] sont les deux fils, s'ils existent, de t[i] :   si p est le nombre de noeuds de l'arbre et si 2 * i = p, t[i] n'a qu'un fils, t[p]. si i est supérieur à p div 2, t[i] est une feuille.

La suite (a1, a2, ... , an) est rangée dans un tableau t[...] correspondant au tableau d'initialisation (le tas). Puis les éléments de ce tableau sont ajouter et traiter un par un dans un arbre avant d'être ajoutés dans un tableau trié en ordre décroissant ou croissant, selon le choix de l'utilisateur.

Notre version de tri par tas comporte les étapes suivantes :

• initialisation : ajouter successivement chacun des n éléments dans le tas t[1..p]; p augmente de 1 après chaque adjonction . A la fin on a un tas de taille p = n.

 
• tant que p est plus grand que 1, supprimer le minimum du tas (p décroît de 1), réorganiser le tas, ranger le minimum obtenue à la (p + 1)^ième place.

Remonter 

Algorithme

L'algorithme proposé est composé de 2 sous algorithmes Ajouter pour la première étape et Supprimer pour la seconde.
 

Algorithme Ajouter Entrée  P : entier ; x : entier // P nombre d'éléments dans le tas, x élément à ajouter               Tas[1..max]  : tableau d'entiers // le tas Sortie  P : entier                Tas[1..max] // le tas Local  j, temp : entiers  début   P ¬ P + 1 ; // incrémentation du nombre d'éléments du tas   j ¬ P ; // initialisation de j à la longueur du tas (position de la dernière feuille)   Tas[P] ¬ x ; // ajout l'élément x à la dernière feuille dans le tas   Tantque (j > 1) et (Tas[j] < Tas[j div 2]) faire ; // tant que l'on est pas arrivé à la racine et que le "fils" est inférieur à son "père", on permute les 2 valeurs          temp ¬ Tas[j] ;          Tas[j] ¬ Tas[j div 2] ;          Tas[j div 2] ¬ temp ;          j ¬ j div 2 ;   finTant FinAjouter Algorithme Supprimer Entrée : P : entier // P nombre d'éléments contenu dans l'arbre               Tas[1..max]  : tableau d'entiers // le tas Sortie : P : entier // P nombre d'éléments contenu dans l'arbre              Tas[1..max]  : tableau d'entiers // le tas              Lemini : entier  // le plus petit de tous les éléments du tas Local i, j, temp : entiers ; début   Lemini ¬ Tas[1] ; // retourne  la racine (minimum actuel) pour stockage éventuel   Tas[1] ¬ Tas[P] ; // la racine prend la valeur de la dernière feuille de l'arbre   P ¬ P - 1 ;    j ¬ 1 ;    Tantque j <= (P div 2) faire       // recherche de l'indice i du plus petit des descendants de Tas[j]       si (2 * j = P ) ou (Tas[2 * j] < Tas[2 * j + 1])                 alors i ¬ 2 * j ;       sinon i ¬ 2 * j +1 ;       Fsi;      // Echange éventuel entre Tas[j] et son fils Tas[i]      si Tlab[j] > Tlab[i] alors             temp ¬ Tlab[j] ;             Tlab[j] ¬ Tlab[i] ;             Tlab[i] ¬ temp ;             j ¬ i ;      sinon Sortir ;      Fsi;   finTant FinSupprimer   Algorithme Tri_par_arbre Entrée  Tas[1..max] // le tas              TabInit[1..max] // les données initiales Sortie    TabTrie[1..max]: tableaux d'entiers //  tableau une fois trié Local    P , i : Entier //  P le nombre d'éléments à trier, i compteur de minimum            Lemin : entier  // le plus petit de tous les éléments du tas Utilise Ajouter, Supprimer début     P ¬ 0;     i ¬ 1 ;    Tantque P < max faire        Ajouter(P,Tas,TabInit[P+1]); // appel de l'algorithme Ajouter    finTant;    Tantque P >= 1 faire        Supprimer(P,Tas,Lemin) ; // appel de l'algorithme Supprimer        TabTrie[i] ¬ Lemin ; // stockage du minimum dans le nouveau tableau        i ¬ i +1    finTant; Fin Tri_par_arbre

Remonter 

Implantation en Java

On utilisera un tas (tableau) global (variable de classe) comme pour les autres exemples de tri, une méthode d'initialisattion du tas, un méthode d'affichage, une méthode Ajouter, une méthode Supprimer, une méthode Tri_Arbre, enfin la méthode main implantera l'appel au tri.

Dans la boucle :

Tantque (j > 1) et (Tas[j] < Tas[j div 2]) faire          temp ¬ Tas[j] ;          Tas[j] ¬ Tas[j div 2] ;          Tas[j div 2] ¬ temp ;          j ¬ j div 2 ;   finTant

l'évaluation complète de l'expression booléenne (j > 1) et (Tas[j] < Tas[j div 2]) engendre un incident dû à un effet de bord. Lorsque l'indice "j" prend par exemple la valeur 1, l'indice "j div 2" vaut alors 0 et cette valeur n'est pas valide  puisque l'indice de tableau varie entre 1..Max.

Nous avons vu dans le cours qu'il était possible de pallier de deux façons à cet inconvenient :

• soit en modifiant la boucle en mettant un test avant

si j>1 alors   Tantque Tas[j] < Tas[j div 2] faire .... finTant

• soit en ajoutant une sentinelle "à gauche dans le tableau" en étendant la borne inférieure à la valeur 0, les indices pouvant alors varier entre 0..Max.

 

 

• Il est possible en Java grâce aux opérateurs d'évaluation booléens optimisés, d'envisager une autre version, utilisez alors le "et"optimisé.

Remonter 

Proposition de squelette de classe Java à implanter :
 

Ci-dessous le code de la méthode main :

Remonter 

---