sur les arbres binaires
Plan du chapitre:
2. Arbres binaires de recherche
1. Implantations des 4 algorithmes de parcours
Implantation de chacun des trois parcours en profondeur par la gauche définissant un ordre implicite (préfixé, infixé, postfixé) sur l'affichage et le traitement des données contenues dans l'arbre. Chaque type de parcours est un cas particulier du parcours général. Nous terminons par le parcours en largeur avec une file Fifo.
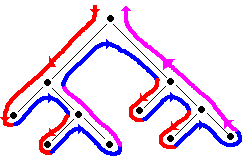
Nous allons implanter en Delphi les 3
algorithmes sous forme de procédures récursives. Nous supposons
que les informations stockées dans un noeud sont du type chaîne
de caractère (string), le traitement consistera ici à
écrire le contenu de la string d'un noeud lorsqu'il est parcouru.
1.1 Implantations avec variables dynamique et classe
Nous proposons deux implantation possibles que le lecteur testera sur sa machine
Implantation en Delphi avec des variables dynamiques :
| type parbre = ^arbre; arbre = record info : string ; filsG, filsD: parbre end; |
Implantation en Delphi avec une classe :
| interface // dans cette classe tous les champ sont publics afin de simplifier l'écriture type TreeBin = class private procedure FreeRecur( x :TreeBin ) ; public Info : string; filsG , filsD : TreeBin; constructor CreerTreeBin(s:string);overload; constructor CreerTreeBin(s:string; fg , fd : TreeBin);overload; destructor Liberer; end; implementation {-------------------- Méthodes
public -------------------------} constructor TreeBin.CreerTreeBin(s : string
; fg, fd : TreeBin); destructor TreeBin.Liberer; end. |
Nous prenons comme exemple sur lequel appliquer les 4 algorithmes, l'arbre
binaire X suivant (chaque noeud a une info de type caractère
stocké dans une string) :
| x = | 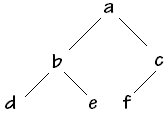
|
Algorithme de parcours en pré-ordre : (ordre préfixé)
| parcourir ( Arbre ) si Arbre ¹Æ alors Traiter-1 (info(Arbre.Racine)) ; parcourir ( Arbre.filsG ) ; parcourir ( Arbre.filsD ) ; Fsi |
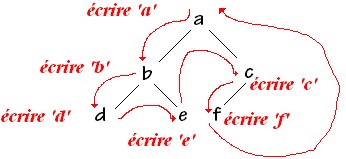
La procédure écrirera succsessivement : abdecf
Préordre en Delphi avec les variables dynamiques :
| procedure prefixe (f : parbre); begin if f <> nil then with f^ do begin write(info); prefixe( filsG ); prefixe( filsD ) end end; |
Préordre en Delphi avec la classe :
| interface type TreeBin = class private procedure FreeRecur( x :TreeBin ) ; procedure PreOrdre ( x : TreeBin); public Info : string; filsG , filsD : TreeBin; constructor CreerTreeBin(s:string);overload; constructor CreerTreeBin(s:string; fg , fd : TreeBin);overload; destructor Liberer; procedure Prefixe; end; implementation {-------------------- Méthodes
public -------------------------} end. |
Algorithme de parcours en post-ordre : (ordre postfixé)
| parcourir ( Arbre ) si Arbre ¹ Æ alors parcourir ( Arbre.filsG ) ; parcourir ( Arbre.filsD ) ; Traiter-3 (info(Arbre.Racine)) ; Fsi |
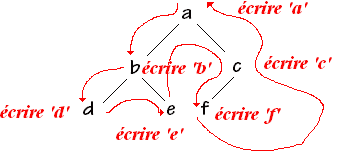
La procédure écrirera succsessivement : debfca
Postordre en Delphi avec les variables dynamiques :
| procedure postfixe (f : parbre); begin if f <> nil then with f^ do begin postfixe( filsG ); postfixe( filsD ); write(info) end end; |
Postordre en Delphi avec la classe :
| interface type TreeBin = class private procedure FreeRecur( x :TreeBin ) ; procedure PreOrdre ( x : TreeBin); procedure PostOrdre ( x : TreeBin); public Info : string; filsG , filsD : TreeBin; constructor CreerTreeBin(s:string);overload; constructor CreerTreeBin(s:string; fg , fd : TreeBin);overload; destructor Liberer; procedure Prefixe; procedure Postfixe; end; implementation {-------------------- Méthodes
public -------------------------} end. |
Algorithme de parcours en ordre symétrique : (ordre infixé)
| parcourir ( Arbre ) si Arbre ¹Æ alors parcourir ( Arbre.filsG ) ; Traiter-2 (info(Arbre.Racine)) ; parcourir ( Arbre.filsD ) ; Fsi |
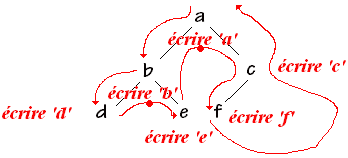
Ordre infixé en Delphi avec les variables dynamiques :
| procedure infixe (f : parbre); begin if f <> nil then with f^ do begin infixe( filsG ); write(info); infixe( filsD ) end end; |
Ordre infixé en Delphi avec la classe :
| interface type TreeBin = class private procedure FreeRecur( x :TreeBin ) ; procedure PreOrdre ( x : TreeBin); procedure PostOrdre ( x : TreeBin); procedure InfixeOrdre ( x : TreeBin); public Info : string; filsG , filsD : TreeBin; constructor CreerTreeBin(s:string);overload; constructor CreerTreeBin(s:string; fg , fd : TreeBin);overload; destructor Liberer; procedure Prefixe; procedure Postfixe; procedure Infixe; end; implementation {-------------------- Méthodes
public -------------------------} end. |
Algorithme de parcours en largeur (hiérarchique)
| Largeur ( Arbre ) si Arbre ¹ Æ alors ajouter Arbre.racine dans Fifo; tantque Fifo ¹ Æ faire prendre premier de Fifo; traiter premier de Fifo; ajouter filsG de premier de Fifo dans Fifo; ajouter filsD de premier de Fifo dans Fifo; ftant Fsi |
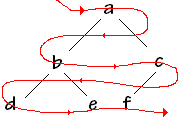
La procédure écrirera succsessivement : abcdef
Implantation en Delphi avec les variables dynamiques et un TList :
type
parbre = ^arbre;
arbre = record
info : string ;
filsG, filsD: parbre
end;
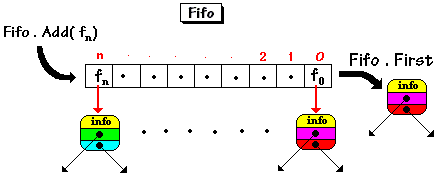
Nous utilisons un objet Delphi de classe TList pour implanter notre Fifo.
| Un TList stocke un tableau de pointeurs (Pointer en Delphi). Un
objet TList est souvent utilisé pour gérer une liste
d'objets. TList introduit des propriétés et méthodes
permettant d'ajouter ou de supprimer des objets de la liste. En particulier
afin d'implanter une file de type Fifo, nous utiliserons les membres suivants
du TList.
méthodes attributs |
Le TList ne contiendra pas les noeuds de l'arbre eux-mêmes mais les pointeurs vers les noeuds (type parbre ici) :
| procedure Largeur ( x : parbre); var Fifo : TList; begin if f <> nil then begin Fifo:=TList.Create; // crée la Fifo Fifo.Add( x ); // ajoute la racine x dans Fifo while Fifo.Count<>0 do begin write(parbre(Fifo.First)^.info); // traitement du premier if parbre(Fifo.First)^.filsG <> nil then Fifo.Add(parbre(Fifo.First)^.filsG); // ajoute le fils gauche du premier dans Fifo if parbre(Fifo.First)^.filsD <> nil then Fifo.Add(parbre(Fifo.First)^.filsD); // ajoute le fils droit du premier dans Fifo Fifo.delete(0); // supprime l'élément de rang 0 (le premier) end; Fifo.Free ; // supprime la Fifo end end; |
On applique la procédure Largeur à l'arbre X afin de parcourir
et d'écrire hiérarchiquement les caractères de chaque
noeud. Ci-dessous le début d'un suivi d'exécution de la procédure
Largeur :
| Instruction exécutée | Action sur le TList Fifo |
| Fifo:=TList.Create; | |
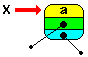
| // ajouter la racine x dans Fifo
Fifo.Add( x ); |
|
| Début de la boucle while : // traitement du premier write(parbre(Fifo.First)^.info) |
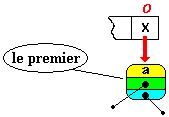
ecrit : a |
| // ajoute le fils gauche du premier dans Fifo
Fifo.Add(parbre(Fifo.First)^.filsG) |
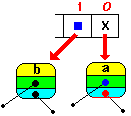
|
| // ajoute le fils droit du premier dans Fifo
Fifo.Add(parbre(Fifo.First)^.filsD) |
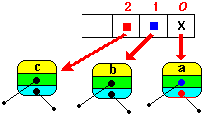
|
| // supprime l'élément de rang
0 (le premier) Fifo.delete(0); |
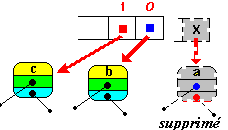
|
| Reprise de la boucle while : // traitement du premier write(parbre(Fifo.First)^.info) etc .... |
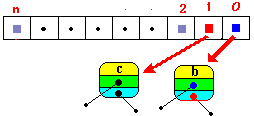
ecrit : b |
{$APPTYPE CONSOLE}
uses sysutils;
type
parbre = ^arbre;
arbre = record
val: char;
g, d: parbre
end;
var
rac,arb1,arb2,arb3,arb4,arb5: parbre;
procedure construit (var rac:parbre; filsg,filsd:parbre;elt:string);
// construit un arbre
begin
if rac=nil then begin
new(rac);
with rac^ do begin
val := elt;
g := filsg;
d := filsd
end;
end
end;{construit}
procedure edite (f: parbre);
{infixe avec parentheses}
begin
if f <> nil then
with f^ do begin
write('(');
edite(g);
write(val);
edite(d);
write(')')
end
end;{edite}
procedure postfixe (f: parbre);
begin
if f <> nil then
with f^ do begin
postfixe(g);
postfixe(d);
write(val);
end
end;{postfixe}
procedure prefixe (f: parbre);
begin
if f <> nil then
with f^ do begin
write(val);
prefixe(g);
prefixe(d)
end
end;{prefixe}
procedure infixe (f: parbre);
begin
if f <> nil then
with f^ do begin
infixe(g);
write(val);
infixe(d);
end
end;{infixe}
procedure Largeur ( f : parbre);
var Fifo : TList;
begin
if f <> nil then begin
Fifo:=TList.Create; // crée la Fifo
Fifo.Add( f ); // ajoute
la racine f dans Fifo
while Fifo.Count<>0 do begin
write(parbre(Fifo.First)^.info); // traitement du premier
if parbre(Fifo.First)^.filsG <>
nil then
Fifo.Add(parbre(Fifo.First)^.filsG);
// ajoute le fils gauche du premier dans Fifo
if parbre(Fifo.First)^.filsD <>
nil then
Fifo.Add(parbre(Fifo.First)^.filsD);
// ajoute le fils droit du premier dans Fifo
Fifo.delete(0); // supprime l'élément de rang 0 (le premier)
end;
Fifo.Free ; // supprime
la Fifo
end
end;{Largeur}
begin {prog-principal}
{ b
/ \
c
f
/ \
d e
}
arb1:=nil;
arb2:=nil;
arb3:=nil;
arb4:=nil;
arb5:=nil;
construit(arb1,nil,nil,'d');
construit(arb2,nil,nil,'e');
construit(arb3,arb1,arb2,'c');
construit(arb4,nil,nil,'f');
construit(arb5,arb3,arb4,'b');
{----------------------------------
g
/ \
h
i
}
arb1:=nil;
arb2:=nil;
arb3:=nil;
construit(arb1,nil,nil,'h');
construit(arb2,nil,nil,'i');
construit(arb3,arb1,arb2,'g');
{----------------------------------
a
/ \
b
g
}
rac:=nil;
construit(rac,arb5,arb3,'a');
{----------------------------------}
{
a
/ \
b
g
/ \
/ \
c
f h i
/ \
d e
}
writeln('lecture parenthésée:');
edite(rac);
writeln;
writeln('lecture notation infixée:');
infixe(rac);
writeln;
writeln('lecture notation postfixée:');
postfixe(rac);
writeln;
writeln('lecture notation préfixée:');
prefixe(rac);
writeln;
writeln('lecture hiérarchique:');
Largeur(rac);
writeln
end.
2. Arbres binaires de recherche
Rappel de la définition : (nommé aussi arbre binaire ordonné horizontalement )
| Un arbre binaire de recherche satisfait aux critères suivants :
|
Nous en avons déjà vu au chap4.7 :
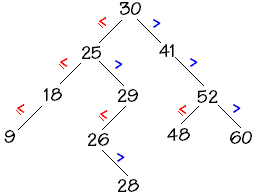
Nous proposons une seule implantation avec le type parbre déjà
défini avec des variables dynamiques au paragraphe précédent.
Rappel de la spécification avec des variables dynamiques :
| type parbre = ^arbre; arbre = record info : string ; filsG, filsD: parbre end; |
Implantation en Delphi avec une classe héritant des TreeBin :
| interface type end; implementation end. |
2.1 Insertion dans un arbre binaire de recherche
Algorithme d'insertion dans un arbre de recherche
| placer l'élément Elt
dans l'arbre Arbre par adjonctions
successives aux feuilles
placer ( Arbre Elt ) si Arbre = Æ alors - tous les éléments
"info" de tous les noeuds du sous-arbre de droite |
Soit par exemple
la liste de caractères alphabétiques : e d f a c b u w , que nous rangeons dans cet ordre d'entrée dans
un arbre binaire de recherche. Ci-dessous le suivi de l'algorithme de placements
successifs de chaque caractère de cette liste dans un arbre de recherche:
| Insertions successives des éléments | Arbre de recherche obtenu |
| placer ( racine , 'e' ) e est la racine de l'arbre. |
e |
| placer ( racine , 'd' ) d < e donc à fils gauche de e. |
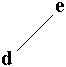
|
| placer ( racine , 'f' ) f > e donc fils droit de e. |
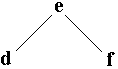
|
| placer ( racine , 'a' ) a < e donc à gauche, a < d donc fils gauche de d. |
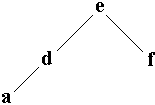
|
| placer ( racine , 'c' ) c < e donc à gauche, c < d donc à gauche, c > a donc fils gauche de a. |
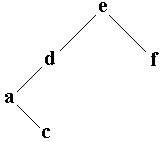
|
| placer ( racine , 'b' ) b < e donc à gauche, b < d donc à gauche, b > a donc à droite de a, b < c donc fils gauche de c. |
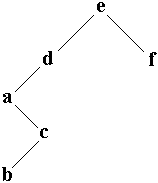
|
| placer ( racine , 'u' ) u > e donc à droite de e, u > f donc fils droit de f. |
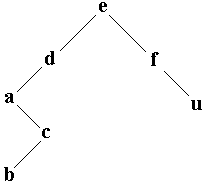
|
| placer ( racine , 'w' ) w > e donc à droite de e, w > f donc à droite de f, w > u donc fils droit de u. |
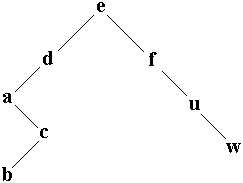
|
Placer en Delphi avec les variables dynamiques :
| procedure placer (var arbre:parbre ; elt:string); {remplissage récursif de l'arbre binaire de recherche par adjonctions successives aux feuilles de l'arbre } begin if arbre = nil then begin new(arbre); arbre^.info:=elt; arbre^.filsG :=nil; arbre^.filsD :=nil end else if elt <= arbre^.info then placer (arbre^.filsG ,elt) else placer (arbre^.filsD , elt); end; |
Placer en Delphi avec la classe TreeBinRech :
| interface type implementation {-------------------- Méthodes
public -------------------------} end. |
Algorithme de recherche dans un arbre de recherche
| chercher l'élément Elt
dans l'arbre Arbre :
Chercher ( Arbre Elt ) : Arbre si Arbre = Æ alors |
Ci-dessous le suivi de l'algorithme de recherche du caractère b dans l'arbre précédent :

Chercher ( Arbre , b ) |
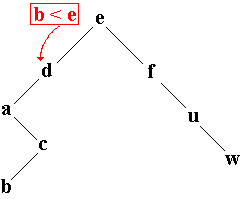
Chercher ( Arbre.filsG , b ) |
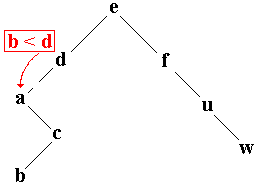
Chercher ( Arbre.filsG , b ) |
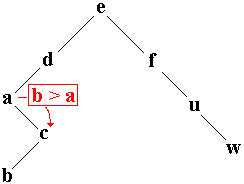
Chercher ( Arbre.filsD , b ) |
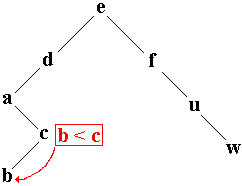
Chercher ( Arbre.filsG , b ) |
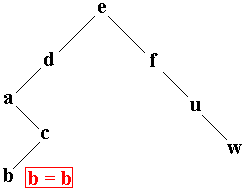
retourner Arbre |
Chercher en Delphi avec les variables dynamiques :
| function Chercher( arbre:parbre; elt:string) : parbre; begin if arbre = nil then begin result := nil; writeln('élément non trouvé') end else if elt = arbre^.info then result := arbre //l'élément est dans ce noeud else if elt < arbre^.info then result := Chercher(arbre^.filsG , elt) //on cherche à gauche else result := Chercher(arbre^.filsD , elt) //on cherche à droite end; |
Chercher en Delphi avec la classe TreeBinRech :
| interface type implementation {-------------------- Méthodes
public -------------------------} end. |
Algorithmes de recherche du max et du min
| chercher le plus grand élément dans l'arbre Arbre : //descendre toujours le plus à droite PlusGrand ( Arbre ) : Arbre
chercher le plus petit élément dans l'arbre Arbre : //descendre toujours le plus à gauche PlusPetit ( Arbre ) : Arbre |
Chercher max et min avec les variables dynamiques :
| function PlusGrand ( arbre:parbre ) : parbre; begin if arbre^.filsD = nil then result := arbre else result := PlusGrand( arbre^.filsD ) //on descend à droite end; function PlusPetit ( arbre:parbre ) : parbre; |
Le lecteur intéressé par l'écriture avec une classe procédera par traduction des programmes ci-après en remplaçant les variables dynamiques comme nous l'avons écrit plus haut, par des objets de classe TreeBinRech qui hérite de la classe TreeBin.
2.4 Suppression dans un arbre
binaire de recherche
Afin de pouvoir supprimer un élément dans un arbre binaire de recherche, il est necessaire de pouvoir d'abord le localiser, ensuite supprimer le noeud ainsi trouvé et procéder à la réorganisation de l'arbre de recherche éventuellement.
Nous supposons que notre arbre binaire de recherche ne possède que des éléments tous distincts (pas de redondance).
Algorithme de suppression dans un arbre de recherche
| supprimer l'élément Elt
dans l'arbre Arbre :
Supprimer ( Arbre Elt ) : Arbre
si Arbre = Æ alors |
Supprimer avec les variables dynamiques :
| function PlusGrand ( arbre : parbre ) : parbre; begin if arbre^.filsD = nil then result := arbre else result := PlusGrand( arbre^.filsD ) //on descend à droite end; procedure Supprimer (var arbre:parbre; elt:string
) ; |
Le lecteur intéressé par l'écriture avec une classe procédera par traduction des programmes ci-après en remplaçant les variables dynamiques par des objets de classe TreeBinRech qui hérite de la classe TreeBin.
Ci-dessous un programme complet reprenant l'exemple précédent avec des variables dynamiques et à exécuter tel quel avec Delphi en mode console :
program arbre_binaire_Rech;
{remplissage d'un arbre binaire de recherche
aussi dénommé arbre binaire ordonné
horizontalement }
{$APPTYPE CONSOLE}
uses sysutils;
type
pointeur = ^noeud;
noeud = record
info:string;
filsGauche:pointeur;
filsDroit:pointeur
end;
var
racine,tree:pointeur;
procedure placer_arbre(var arbre:pointeur; elt:string);
{remplissage récursif de l'arbre binaire de
recherche}
begin
if arbre=nil then
begin
new(arbre);
arbre^.info:=elt;
arbre^.filsGauche:=nil;
arbre^.filsDroit:=nil
end
else
{ - tous les éléments "info"
de tous les noeuds du sous-arbre de gauche
sont inférieurs ou
égaux à l'élément "info" du noeud en cours (arbre)
- tous les éléments
"info" de tous les noeuds du sous-arbre de droite
sont supérieurs à
l'élément "info" du noeud en cours (arbre)
}
if elt<=arbre^.info then placer_arbre(arbre^.filsGauche,elt)
else placer_arbre(arbre^.filsDroit,elt);
end;
procedure infixe(branche:pointeur);
{lecture symétrique de l'arbre binaire}
begin
if branche<>nil then
begin
infixe(branche^.filsGauche);
write(branche^.info,' ');
infixe(branche^.filsDroit);
end
end;
function ChercherArbre( arbre:pointeur; elt:string):pointeur;
begin
if arbre=nil then
begin
ChercherArbre:=nil;
writeln('élément: '+elt+' non trouvé.')
end
else
if elt = arbre^.info then ChercherArbre:=arbre
else
if elt < arbre^.info then ChercherArbre:=ChercherArbre(arbre^.filsGauche,elt)
else ChercherArbre:=ChercherArbre(arbre^.filsDroit,elt)
end;
function PlusGrand ( arbre : pointeur ) : pointeur;
begin
if arbre^.filsDroit = nil then result :=
arbre
else result := PlusGrand( arbre^.filsDroit ) //on descend à droite
end;
procedure Supprimer (var arbre:pointeur; elt:string
) ;
var Node,Loc:pointeur;
begin
if arbre <> nil then
if elt < arbre^.info then
Supprimer (arbre^.filsGauche,
elt )
else
if elt > arbre^.info then
Supprimer (arbre^.filsDroit, elt
)
else // elt = arbre^.info
if arbre^.filsGauche = nil then
begin
Loc:=arbre;
arbre := arbre^.filsDroit;
dispose(Loc)
end
else
if arbre^.filsDroit = nil
then
begin
Loc:=arbre;
arbre := arbre^.filsGauche;
dispose(Loc)
end
else
begin
Node := PlusGrand ( arbre^.filsGauche
);
Loc:=Node;
arbre^.info := Node^.info;
arbre^.filsGauche :=Node^.filsGauche;
dispose(Loc)
end
end;
begin
racine:=nil;
{soit la liste entrée : e d f a c
b u w }
placer_arbre(racine,'e');
placer_arbre(racine,'d');
placer_arbre(racine,'f');
placer_arbre(racine,'a');
placer_arbre(racine,'c');
placer_arbre(racine,'b');
placer_arbre(racine,'u');
placer_arbre(racine,'w');
{on peut aussi entrer 8 éléments
au clavier
for i:=1 to 8 do
begin
readln(entree);
placer_arbre(racine,entree);
end; }
supprimer(racine, 'b');
writeln('parcours infixé (ou symétrique):');
infixe(racine);
writeln;
tree:=ChercherArbre(racine,'c');
if tree<>nil then writeln( 'recherche de
"c" : ok');
tree:=ChercherArbre(racine,'g');
if tree<>nil then writeln( 'recherche de "g" :
ok');
{ Notons que le parcours infixé produit
une liste des
éléments info,
classée par ordre croissant
}
end.
Il est conseillé au lecteur de reprendre ce programme
en utilisant la classe TreeBinRech décrite plus haut.