4.9. Arbres binaires et expressions arithmétiques
    un exercice entièrement traité

    Plan du chapitre:

    1. Expressions arithmétiques et arbre binaire

       
      1.1 Etape n°1 le processus d'analyse
      • étude de la règle-1
      • étude de la règle-2
      • étude de la règle-3
      • programme Delphi


      1.2 Etape n°2 la génération de l'arbre abstrait

      • génération pour la règle-1
      • génération pour la règle-2
      • génération pour la règle-3
      • programme Delphi
       

     

    1. Expressions arithmétiques et arbre binaire

    Nous allons détailler la démarche de création d'un programme ayant pour but de construire et de parcourir un arbre de syntaxe abstrait des expressions arithmétiques fondées sur une C-grammaire.

    Nous procédons par étapes séparées afin de bien faire comprendre le processus de conception du programme. La première étape consiste à écrire un programme d'analyse des expressions permettant de repérer les variables représentées par des lettres et les opérateurs. Il ne s'agit pas ici d'un processus lexical, mais d'un processus syntaxique déjà abordé au chapitre 3 du cours.

    Une fois le programme en version analyse syntaxique élaboré, nous passons à l'étape de génération de l'arbre binaire abstrait représentant l'expression en cours d'analyse.

     Grammaire des expressions utilisée :

            Vn = {<expr>, <terme>,  <facteur>, <caractère>  }
            Vt = { + ,-  , (  , ) ,*  , /  , a  ,..., z}

    Axiome : <expr>

    Règles :

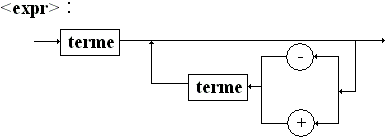
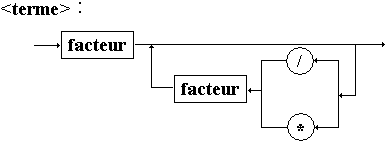
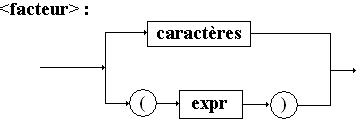
    <caractères> ::= a| b | c | ..... | z

    Remonter


    1.1 Etape n°1 le processus d'analyse

    Nous suivons la stratégie d'analyse citée dans le chapitre 3.2.
     

    • Afin d'améliorer le traitement des données, nous ajoutons une sentinelle à l'expression, soit le caractère '.' choisi comme sentinelle.
    • Afin de simplifier le code (l'objectif principal étant la construction de l'arbre abstrait) nous n'analysons que des expressions correctes, donc nous ne nous préoccuperons pas des tests d'erreurs.


    Nous procédons donc règles par règles et nous donnons au lecteur l'algorithme et l'implantation en Delphi de chaque bloc associé à une règle :
     
  • étude de la règle-1
  • étude de la règle-2
  • étude de la règle-3
  • programme Delphi
    		•

    1.1.1  étude de la Règle-1 :


    Bloc Analyser expr :
    si SymLu Î Init(terme) alors
     Analyser terme ;
     tantque SymLu Î Init( {+,-} )faire
       Symsuivant;
       Analyser terme ;
     ftant;
     //si SymLu Ï Init( {'.'} )Alors Erreur fsi
    sinon Erreur
    fsi
    Implantation en Delphi :

    procedure expr;
    begin
        terme;
        while SymLu in ['+', '-'] do
          begin
            Symsuivant;
            terme;
          end
    end;{expr}

    Remonter

      1.1.2  étude de la Règle-2 :


    Bloc Analyser terme :
    si SymLu Î Init(facteur) alors
     Analyser facteur ;
     tantque SymLu Î Init( { *, / } )faire
       Symsuivant;
       Analyser facteur ;
     ftant;
     //si SymLu Ï Init( {+,-,*,/,'.'} )Alors Erreur fsi
    fsi
    Implantation en Delphi :

    procedure terme;
    begin
          facteur;
          while SymLu in ['*', '/'] do
            begin
              Symsuivant;
              facteur;
            end
     end;{terme}

    Remonter

    1.1.3 étude de la Règle-3 :


    Bloc Analyser facteur :
    si SymLu Î Init(caractères) alors
     Symsuivant
    sinon
     si SymLu Î Init({'('}) alors
       Symsuivant;
       Analyser expr ;
       si SymLu Î Init({')'}) alors
         Symsuivant;
       fsi
     sinon Erreur
     fsi
    fsi
    Implantation en Delphi :

    procedure facteur ;
    begin
          if SymLu = '(' then
            begin
              Symsuivant;
              expr;
              if SymLu = ')' then
                Symsuivant
            end
          else // on est dans caractères car: expression correcte
            begin
              Symsuivant
            end
    end;{facteur}

    Remonter

    1.1.4  programme complet en Delphi :

    Voici le programme Delphi obtenu pour analyser une expression correctement écrite, pour l'instant si l'on exécute ce programme tel quel, il ne produira rien, car nous sommes encore à la première étape du travail.
     
    program expression;
    var
        SymLu: char;
        numcar: integer;
        chaine: string;

      procedure init;
      begin
        numcar := 0;
      end;

     procedure Symsuivant;
     begin
        numcar := numcar + 1;
        SymLu := chaine[numcar]
     end;

    procedure expr;
    begin
        terme;
        while SymLu in ['+', '-'] do
          begin
            Symsuivant;
            terme;
          end
    end;{expr}

    procedure terme;
    begin
          facteur;
          while SymLu in ['*', '/'] do
            begin
              Symsuivant;
              facteur;
            end
     end;{terme}

    procedure facteur ;
    begin
          if SymLu = '(' then
            begin
              Symsuivant;
              expr;
              if SymLu = ')' then
                Symsuivant
            end
          else // on est dans caractères car: expression correcte
            begin
              Symsuivant
            end
    end;{facteur}

    begin
      init;
      writeln('entrez une expression:');
      readln(chaine);
      chaine := concat(chaine, '.');
      Symsuivant;
      expr(x);
    end.

    Remonter

    1.2 Etape n°2 la construction de l'arbre abstrait

    Nous allons stocker les différents symboles de l'expression au fur et à mesure de son analyse, dans un arbre binaire représentant l'arbre abstrait de l'expression comme nous l'avons déjà vu au chapitre 4.7 .
     
  • génération pour la règle-1
  • génération pour la règle-2
  • génération pour la règle-3
  • programme Delphi
  • trace pas à pas
    		•

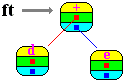
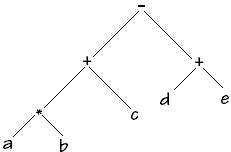
    Pour l'exemple à partir de l'expression a*b + c-(d+e) nous construirons l'arbre abstrait figuré ci-dessous :


     

    Implantation de la structure en Delphi avec variables dynamiques :
     
    type
        parbre = ^arbre;
        arbre = record
                       val: char;
                       g, d: parbre
               end;

    Nous proposons d'écrire une fonction de construction d'un arbre (un constructeur d'arbre)
     

    • La fonction reçoit en entrée 3 paramètres correspondant au contenu d'un noeud :
      • la valeur (un char ici),
      • le pointeur (ou référence) vers le fils gauche de ce noeud,
      • et  le pointeur (ou référence) vers le fils droit de ce noeud.
    • La fonction renvoie un fois le noeud construit, un pointeur (ou référence) sur le noeud nouvellement construit.


    Voici le code de la fonction 'Construit' proposée selon le type parbre défini plus haut :
     
    function Construit (c: char; fg, fd: parbre): parbre;
    var  floc: parbre;
    begin
        new(floc);
        with floc^ do
        begin
            val := c;
            g := fg;
            d := fd
        end;
        construit := floc
    end;{construit}

    Ci-dessous sur deux exemples montrons ce que produit la function Construit(..).

    Exemple -1 : la construction d'un noeud ayant deux descendants
    (un sous-arbre gauche nommé fg, et un sous-arbre droit nommé fd )


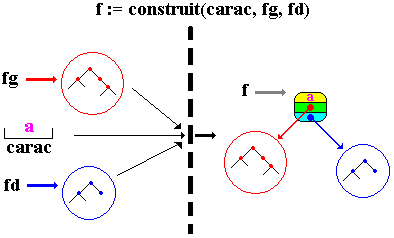
    A la fin de la construction la fonction construit a relié l'arbre gauche rouge avec l'arbre droit bleu dans le noeud pointé par f, respectivement comme sous-arbre gauche rouge et comme sous-arbre droit bleu, le champ valeur du noeud f contient le caractère 'a'.

    Exemple -2 : la construction d'une feuille

    Remonter

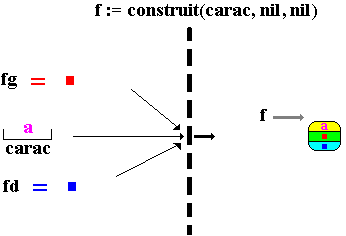
    1.2.1  génération pour la Règle-1 :

    Bloc générer arbre - expr :
    si SymLu Î Init(terme) alors
     Analyser terme ;
     tantque SymLu Î Init( {+,-} )faire
       Symsuivant;
       Analyser terme ;
       construire arbre
     ftant;
     //si SymLu Ï Init( {'.'} )Alors Erreur fsi
    sinon Erreur
    fsi
    Implantation en Delphi :

    procedure expr (var f: parbre) ;
    var
          carloc: char;
          ft: parbre;
     begin
        terme(f);
        while SymLu in ['+', '-'] do
          begin
            carloc := SymLu;
            Symsuivant;
            terme(ft);
            f := construit(carloc, f, ft){construction de l'arbre}
          end
    end;{expr}

    Remonter

    1.2.2  génération pour la Règle-2 :

    Bloc générer arbre -  terme :
    si SymLu Î Init(facteur) alors
     Analyser facteur ;
     tantque SymLu Î Init( { *, / } )faire
       Symsuivant;
       Analyser facteur ;
       construire arbre
     ftant;
     //si SymLu Ï Init( {+,-,*,/,'.'} )Alors Erreur fsi
    fsi
    Implantation en Delphi :

    procedure terme (var f: parbre);
          var
            carloc: char;
            floc: parbre;
        begin
          facteur(f);
          while SymLu in ['*', '/'] do
            begin
              carloc := SymLu;
              Symsuivant;
              facteur(floc);
              f := construit(carloc, f, floc){construction de l'arbre}
            end
        end;{terme}

    Remonter

    1.2.3  génération pour la Règle-3 :

    Bloc générer arbre -  facteur :
    si SymLu Î Init(caractères) alors
     Symsuivant
    sinon
     si SymLu Î Init({'('}) alors
       Symsuivant;
       Analyser expr ;
       si SymLu Î Init({')'}) alors
         Symsuivant;
       fsi
     sinon Erreur
     fsi
    fsi
    Implantation en Delphi :

    procedure facteur (var f: parbre);
    begin
          if SymLu = '(' then
            begin
              Symsuivant;
              expr(f);
              if SymLu = ')' then
                Symsuivant
            end
          else
            begin
              f := construit(SymLu, nil, nil); {construction de l'arbre }
              Symsuivant
            end
    end;{facteur}

    Remonter

    1.2.4  programme complet en Delphi :

    Voici un programme Delphi obtenu pour engendrer un arbre abstrait d'une expression correctement écrite; ici les procédures terme et facteur ont été incluses dans la partie déclaration de la procédure expr, mais elles peuvent être dissociées et se retrouver au même niveau de déclaration sans rien changer au fonctionnement du programme.
     
    program expression;
    {les expressions entrées sont correctes }
      type
        parbre = ^arbre;
        arbre = record
                       val: char;
                       g, d: parbre
               end;
      var
        x: parbre;
        SymLu: char;
        numcar: integer;
        chaine: string;

      procedure init;
      begin
        numcar := 0;
        x := nil;
      end;

      function construit (c: char; fg, fd: parbre): parbre;
        var
          floc: parbre;
      begin
        new(floc);
        with floc^ do
          begin
            val := c;
            g := fg;
            d := fd
          end;
        construit := floc
      end;{construit}

      procedure Symsuivant;
      begin
        numcar := numcar + 1;
        SymLu := chaine[numcar]
      end;

     {construction d'un arbre d'expressions à partir de la grammaire :}
      procedure expr (var f: parbre);
        var
          carloc: char;
          ft: parbre;
        procedure facteur (var f: parbre);
        begin
          if SymLu = '(' then
            begin
              Symsuivant;
              expr(f);
              if SymLu = ')' then
                Symsuivant
            end
          else
            begin
              f := construit(SymLu, nil, nil); {construction de l'arbre }
              Symsuivant
            end
        end;{facteur}

        procedure terme (var f: parbre);
          var
            carloc: char;
            floc: parbre;
        begin
          facteur(f);
          while SymLu in ['*', '/'] do
            begin
              carloc := SymLu;
              Symsuivant;
              facteur(floc);
              f := construit(carloc, f, floc){construction de l'arbre}
            end
        end;{terme}

      begin{expr}
        terme(f);
        while SymLu in ['+', '-'] do
          begin
            carloc := SymLu;
            Symsuivant;
            terme(ft);
            f := construit(carloc, f, ft){construction de l'arbre}
          end
      end;{expr}

    begin
      init;
      writeln('entrez une expression:');
      readln(chaine);
      chaine := concat(chaine, '.');
      Symsuivant;
      expr(x);
    end.

    Suivons à titre d'exemple la construction par le programme précédent, de l'arbre abstrait de l'expression déjà citée plus haut soit : a*b + c-(d+e).

    Nous effectuons une trace pas à pas du début de l'exécution sur l'expression :
     
    Procédures appelées Résultat produit 
    readln(chaine); chaine = a*b + c-(d+e).
    init; x = nil
    Symsuivant SymLu = a   , dans a*b + c-(d+e).
    expr(x)
      |terme(x)
      |  |facteur(x)
      |  |    |x := construit(SymLu, nil, nil);
      |  |    |Symsuivant

    SymLu = *  , dans a*b + c-(d+e).
    expr(x)
      |terme(x)
      |  |facteur(x)
      |  |SymLu in ['*', '/'] = true
      |     carloc := SymLu;
      |     Symsuivant;
      |     facteur(floc);    		 carloc = *
    SymLu = b  , dans a*b + c-(d+e).
    floc = nil
    expr(x)
      |terme(x)
      |  |facteur(floc);
      |  | |floc := construit(SymLu, nil, nil);
      |  |    |Symsuivant    		 carloc = *

    SymLu = +  , dans a*b + c-(d+e).
    expr(x)
      |terme(x) 
      |  |facteur(floc);
      |  |x := construit(carloc, x, floc)    		 carloc = *
    expr(x)
      |terme(x);
      |SymLu in ['+', '-'] = true
      |    carloc := SymLu;
      |    Symsuivant;
      |    terme(ft);     		 carloc = +
    SymLu = c  , dans a*b + c-(d+e).
    ft = nil
    expr(x)
      |terme(x)
      |  |terme(ft)
      |  |  |facteur(ft);
      |  |  |     |ft := construit(SymLu, nil, nil);
      |  |  |     |Symsuivant    		 carloc = +


    SymLu = -  , dans a*b + c - (d+e).
    expr(x)
      |terme(x)
      |  |terme(ft)
      |  |  |facteur(ft);
      |  |  |x := construit(carloc, x, ft)    		 carloc = +
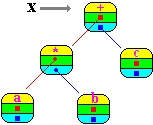
    expr(x)
      |terme(x)
      |  |terme(ft)
      |  |facteur(ft)
      |  |  |SymLu in ['*', '/'] = false
      |SymLu in ['+', '-'] = true
      |   carloc := SymLu;
      |   Symsuivant;
      |   |terme(ft);     		 carloc = -
    SymLu = (  , dans a*b + c-(d+e).
    ft = nil
    expr(x)
      |terme(x)
      |  |facteur(ft);
      |  |     |SymLu = '('  = true 
      |  |          Symsuivant;
      |  |          |expr(ft);
      |  |            |terme(ft);
      |  |            |  |facteur(ft);    		 carloc = -
    SymLu = d  , dans a*b + c-(d+e).
    ft = nil
    expr(x)
      |terme(x)
      |  |facteur(ft)
      |  |  |expr(ft)
      |  |  |  |terme(ft)
      |  |  |  |  |facteur(ft)
      |  |  |  |  | |ft := construit(SymLu, nil, nil);
      |  |  |  |  | |Symsuivant;    		 carloc = -

    SymLu = +  , dans a*b + c-(d+e).
    expr(x)
      |terme(x)
      |  |facteur(ft)
      |  |  |expr(ft)
      |  |  |  |terme(ft)
      |  |  |  |  |facteur(ft)
      |  |  |  |  |SymLu in ['*', '/'] = false
      |  |  |  |SymLu in ['+', '-'] = true
      |  |  |  |    carloc := SymLu;
      |  |  |  |    Symsuivant;
      |  |  |  |    |terme(ft); 
      |  |  |  |    |   |facteur(ft);
    dans la pile :
    ----------------
    carloc = -

    -----------------------

    carloc = +

    SymLu = e  , dans a*b + c-(d+e).

    ft = nil
    expr(x)
      |terme(x)
      |  |facteur(ft)
      |  |  |expr(ft)
      |  |  |  |terme(ft)
      |  |  |  |  |terme(ft)
      |  |  |  |  |  |facteur(ft)
      |  |  |  |  |  |  |ft := construit(SymLu, nil, nil);
      |  |  |  |  |  |  |Symsuivant;    		 dans la pile :
    ----------------
    carloc = -

    -----------------------

    carloc = +


    SymLu = )  , dans a*b + c-(d+e).
     
    expr(x)
      |terme(x)
      |  |facteur(ft)
      |  |  |expr(ft)
      |  |  |  |terme(ft)
      |  |  |  |  |terme(ft)
      |  |  |  |  |  |facteur(ft)
      |  |  |  |  |  |  |ft := construit(carloc , ft , ft )
      |  |  |  |  | |SymLu in ['*', '/'] = false    		 dans la pile :
    ----------------
    carloc = -

    ----------------------------
     


     
    expr(x)
      |terme(x)
      |  |facteur(ft)
      |  |  |expr(ft)
      |  |  |  |terme(ft)
      |  |  |  |SymLu in ['+', '-'] = false
      |  |x := construit(carloc, x, ft)
      |SymLu in ['*', '/'] = false
    Fin
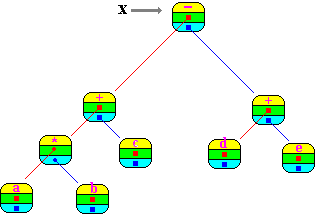
    Arbre abstrait obtenu après exécution :

    Si le lecteur souhaite visualiser les contenus des arbres abstraits, il peut utiliser les 3 parcours en profondeur vus au chapitre 4.8, nous listons ci-dessous les 3 procédures associées au type parbre de l'exercice ainsi que le corps du programme principal appellant ces procédures :
     
    program expression;
    {les expressions sont correctes et elles sont lues sous les 3 formes
    in,post et pré-fixées }
      type
        parbre = ^arbre;
        arbre = record
                       val: char;
                       g, d: parbre
               end;
      var
        x: parbre;
        SymLu: char;
        numcar: integer;
        chaine: string;

      procedure init;
      begin
        numcar := 0;
        x := nil;
      end;

      function construit (c: char; fg, fd: parbre): parbre;
        var
          floc: parbre;
      begin
        new(floc);
        with floc^ do
          begin
            val := c;
            g := fg;
            d := fd
          end;
        construit := floc
      end;{construit}

      procedure Symsuivant;
      begin
        numcar := numcar + 1;
        SymLu := chaine[numcar]
      end;

     {construction d'un arbre d'expressions à partir de la grammaire :}
      procedure expr (var f: parbre);
        var
          carloc: char;
          ft: parbre;
        procedure facteur (var f: parbre);
        begin
          if SymLu = '(' then
            begin
              Symsuivant;
              expr(f);
              if SymLu = ')' then
                Symsuivant
            end
          else
            begin
              f := construit(SymLu, nil, nil); {construction de l'arbre }
              Symsuivant
            end
        end;{facteur}

        procedure terme (var f: parbre);
          var
            carloc: char;
            floc: parbre;
        begin
          facteur(f);
          while SymLu in ['*', '/'] do
            begin
              carloc := SymLu;
              Symsuivant;
              facteur(floc);
              f := construit(carloc, f, floc){construction de l'arbre}
            end
        end;{terme}

      begin{expr}
        terme(f);
        while SymLu in ['+', '-'] do
          begin
            carloc := SymLu;
            Symsuivant;
            terme(ft);
            f := construit(carloc, f, ft){construction de l'arbre}
          end
      end;{expr}

     procedure edite (f: parbre);
      {infixe parenthesee}
      begin
        if f <> nil then
          with f^ do
            begin
              write('(');
              edite(g);
              write(val);
              edite(d);
              write(')')
            end
      end;

      procedure postfixe (f: parbre);
     {sert dans les machine a piles a la compilation}
      begin
        if f <> nil then
          with f^ do
            begin
              postfixe(g);
              postfixe(d);
              write(val);
            end
      end;

      procedure prefixe (f: parbre);
      begin
        if f <> nil then
          with f^ do
            begin
              write(val);
              prefixe(g);
              prefixe(d)
            end
      end;

      procedure infixe (f: parbre);
      begin
        if f <> nil then
          with f^ do
            begin
              infixe(g);
              write(val);
              infixe(d);
            end
      end;

    begin
      init;
      writeln('entrez une expression:');
      readln(chaine);
      chaine := concat(chaine, '.');
      Symsuivant;
      expr(x);
      writeln('Expression parenthésée:');
      edite(x);
      writeln;
      writeln('Expression notation infixée:');
      infixe(x);
      writeln;
      writeln('Expression notation postfixée:');
      postfixe(x);
      writeln;
      writeln('Expression notation préfixée:');
      prefixe(x);
      writeln
    end.

    Remonter