4.6.Quelques méthodes de tri internes
comparées

Plan du chapitre:

1. Complexité d'un algorithme

     
    1.1 Notions de complexité temporelle et spatiale
    1.2 Mesure de la complexité temporelle d'un algorithme
    1.3 Notation de Landau O(n)


2. Trier des tableaux en mémoire centrale

     
    2.1 Tri interne, tri externe
    2.2 Des algorithmes classiques de tri interne


3. Rechercher dans un tableau
 

3.1 Recherche dans un tableau non trié
3.2 Recherche dans un tableau trié



 

1. Complexité d'un algorithme et performance

Nous faisons la distinction entre les méthodes (algorithmes) de tri d'un grand nombre d'éléments (plusieurs milliers ou plus), et le tri de quelques éléments (quelques dizaines, voir quelques centaines ). Pour de très petits nombres d'éléments, la méthode importe peu. Il est intéressant de pouvoir comparer différents algorithmes de tris afin de savoir quand les utiliser. Ce que nous énonçons dans ce paragraphe s'applique en général à tous les algorithmes et en particulier aux algorithmes de tris qui en sont une excellente illustration.
 

1.1 Notions de complexité temporelle et spatiale
 
L'efficacité d'un algorithme est directement liée au programme à implémenter sur un ordinateur. Le programme va s'exécuter en un temps fini et va mobiliser des ressources mémoires pendant son exécution; ces deux paramètres se dénomment complexité temporelle et complexité spatiale.

Dès le début de l'informatique les deux paramètres "temps d'exécution" et "place mémoire" ont eu une importance à peu près égale pour comparer l'efficacité relative des algorithmes. Il est clair que depuis que l'on peut, à coût très réduit avoir des mémoires centrales d'environ 1 Giga octets dans une machine personnelle, les soucis de place en mémoire centrale qui s'étaient fait jour lorsque l'on travaillait avec des mémoires centrales de 128 Kilo octets (pour des gros matériels de recherche des années 70) sont repoussés psychologiquement plus loin pour un utilisateur normal. Comme c'est le système d'exploitation qui gère la mémoire disponible ( RAM, cache, virtuelle etc...), les analyses de performances de gestion de la mémoire peuvent varier pour le même programme.

Le facteur temps d'exécution reste l'élément qualitatif le plus perceptible par l'utilisateur d'un programme ne serait ce que parce qu'il attend derrière son écran le résultat d'un travail qui représente l'exécution d'un algorithme.

L'informatique reste une science de l'ingénieur ce qui signifie ici, que malgré toutes les études ou les critères théoriques permettant de comparer l'efficacité de deux algorithmes dans l'absolu, dans la pratique nous ne pourrons pas dire qu'il y a un meilleur algorithme pour résoudre tel type de problème. Une méthode pouvant être lente pour certaines configurations de données et dans une autre application qui travaille systématiquement sur une configuration de données favorables la méthode peut s'avérer être la "meilleure".

La recherche de la performance à tout prix est aussi inefficace que l'attitude contraire.

Prenons à notre compte les recommandations de R.Sedgewick :
Quels que soit le problème mettez d'abord en oeuvre l'algorithme le plus simple, solution du problème, car 
le temps nécessaire à l'implantation et à la mise au point d'un algorithme "optimisé" peut être bien plus important que le temps requis pour simplement faire fonctionner un programme légèrement moins rapide.

Il nous faut donc un outil permettant de comparer l'efficacité ou la complexité d'un algorithme à celle d'un autre algorithme résolvant le même problème.
 

1.2 Mesure de la complexité temporelle d'un algorithme


Nous prenons le parti de nous interesser uniquement au temps théorique d'exécution d'un algorithme. Pourquoi théorique et non pratique ? Parce que le temps pratique d'exécution d'un programme, comme nous l'avons signalé plus haut dépend :
 
  • de la machine (par exemple processeur travaillant avec des jeux d'instructions optimisées ou non), 
  • du système d'exploitation (par exemple dans la gestion multi-tâche des processus), 
  • du compilateur du langage dans lequel l'algorithme sera traduit (compilateur natif pour un processeur donné ou non),
  • des données utilisées par le programme (nature et/ou taille),
  • d'un facteur intrinsèque à l'algorithme.

Nous souhaitons donc pouvoir utiliser un instrument mathématique de mesure qui rende compte de l'efficacité spécifique d'un algorithme indépendamment de son implantation en langage évolué sur une machine. Tout en sachant bien que certains algorithmes ne pourront pas être analysés ainsi soit parce que mathématiquement cela est impossible, soit parce que les configurations de données ne sont pas spécifiées d'un manière précise, soit patrce que le temps mis à analyser correctement l'algorithme dépasserait le temps de loisir et de travail disponible du développeur !

Notre instrument, la complexité temporelle, est fondé sur des outils abstraits (qui ont leur correpondance concrète dans un langage de programmation). L'outil le plus connu est l'opération élémentaire (quantité abstraite définie intuitivement ou d'une manière évidente par le développeur).

Notion d'opération élémentaire
Une opération élémentaire est une opération fondamentale d'un algorithme si le temps d'exécution est directement lié (par une formule mathématique ou empirique) au nombre de ces opérations élémentaires. Il peut y avoir plusieures opérations élémentaires dans un même algorithme.

Nous pourrons ainsi comparer deux algorithmes résolvant le même problème en comparant ce nombre d'opérations élémentaires effectuées par chacun des deux algorithmes.
 

1.2.1 La complexité temporelle
est le décompte du nombre d'opérations élémentaires effectuées par un algorithme donné. 

Décompte du nombre d'opérations élémentaires effectuées par un algorithme donné

Il n'existe pas de méthodologie systématique (art de l'ingénieur) permettant pour un algorithme quelconque de compter les opérations élémentaires. Toutefois des règles usuelles sont communément admises par la communauté des informaticiens qui les utilisent pour évaluer la complexité temporelle.

Soient  i1 , i2 , ... , ik des instructions algorithmiques (affectation, itération, condition,...)

Soit une opération élémentaire dénotée OpElem, supposons qu'elle apparaisse n1 fois dans l'instruction i1,  n2 fois dans l'instruction i2, ... nk fois dans l'instruction ik. Nous noterons Nb(i1) le nombre n1, Nb(i2) le nombre n2  etc. La fonction Nb (ik ) indiquant le nombre d'opérations  élémentaires dénoté OpElem contenu dans l'instruction algorithmique ik.

Nb( ) :  Instruction -----> Entier
 

1.2.2 Complexité temporelle d'une séquence d'instructions

Soit S la séquence d'exécution des instructions i1 ; i2 ; ... ; ik : 

Le nombre d'opérations élémentaires  OpElem de S, Nb(S)  est égal à la somme des nombres: n1 + n2 + ... + nk
S   =   début
    i1 ;
    i2 ;
      ... ; 
    ik
 fin

Donc  :
 Nb( S )  = å Nb(ip)

 

1.2.3 Complexité temporelle d'une instruction conditionnelle

Dans les instructions conditionnelles étant donné qu'il n'est pas possible d'une manière générale de déterminer systématiquement quelle partie de l'instruction est exécutée (le alors ou le sinon), on prend donc un majorant :
 
Cond = si Expr alors E1 
sinon E2
fsi

Donc  :
Nb( Cond ) < Nb( Expr) +max ( Nb( E1 ) , Nb( E2 ) )

 

1.2.4 Complexité temporelle d'une itération finie bornée

Dans le cas d'une boucle finie bornée (comme pour...fpour) contrôlée par une variable d'indice "i", l'on connaît le nombre exact d'itérations noté Nbr_d'itérations de l'ensemble des instructions composant le corps de la boucle dénotées S (où S est une séquence d'instructions), l'arrêt étant assuré par la condition de sortie Expr(i) dépendant de la variable d'indice de boucle i. La complexité est égale au produit du nombre d'itérations par la somme de la complexité de la séquence d'instructions du corps et de celle de l'évaluation de la condition d'arrêt Expr(i). Lorsque le nombre d'itération n'est pas connu mais seulement majoré alors on obtient un majorant de la complexité de la boucle (le majorant correspond à la complexité dans le pire des cas).
 
Iter = Itération Expr(i)
  S
finItér

Donc  :
Nb( Iter ) = [ Nb( S) + Nb(Expr(i)) ] x Nbr_d'itérations

Exemple dans le cas d'une boucle pour...fpour :
Iter = pour i<-- a jusquà b faire
    i1 ;
    i2 ;
      ... ; 
    ik
fpour

La complexité de la condition d'arrêt est par définition de 1 (<=> le temps d'exécution de l'opération effectuée en l'occurence un test, ne dépend ni de la taille des données ni de leurs valeurs), en notant |b-a| le nombre exact d'itérations exécutées (lorsque les bornes sont des entiers |b-a| vaut exactement la valeur absolue de la différence des bornes) nous avons :

Nb( Iter ) = ( å Nb(ip) + 1 ) . |b-a|

Lorsque le nombre d'itérations n'est pas connu mais seulement majoré ( nombre noté Majorant_Nbr_d'itérations ), alors on obtient un majorant de la complexité de la boucle (le majorant correspond à la complexité dans le pire des cas).
 
Complexité temporelle au pire :
Majorant_Nb( Iter ) = [ Nb( S) + Nb(Expr(i)) ] x Majorant_Nbr_d'itérations

 

1.3 Notation d Landau O(n)

Nous avons admis l'hypothése qu'en règle générale la complexité en temps dépend de la taille n des données (plus le nombre de données est grand plus le temps d'exécution est long). Cette remarque est d'autant plus proche de la réalité que nous étudierons essentiellement des algorithmes de tri dans lesquels les n données sont représentées par une liste à n éléments. Afin que notre instrument de mesure et de comparaison d'algorithmes ne dépende pas de la machine physique, nous n'exprimons pas le temps d'exécution en unités de temps (millisecondes etc..) mais en unité de taille des données.

Nous ne souhaitons pas ici rentrer dans le détail mathématique des notations O(f(n))  de Landau sur les infiniments grands équivalents, nous donnons seulement une utilisation pratique de cette notation :

Pour une fonction f (n) dépendant de la variable  n, on écrit :

f est O(g(n)) g(n) où g est elle-même une fonction de la variable entière n, et l'on lit f est de l'ordre de grandeur de g(n) ou plus succinctement f est d'ordre g(n), lorsque :
 
pour tout valeur entière de n, il existe deux constantes a et b positives telles que 

a.g(n) < f(n) < b.g(n) 

Ce qui signifie que lorsque n tend vers l'infini (n devient très grand en informatique) le rapport f(n)/g(n) reste borné.

Exemple :
 f(n) = 3n² - 7n +4
 g(n) = n²
Lorsque n tend vers l'infini le rapport f(n)/g(n) tend vers 3, il est donc borné.
 f(n)/g(n) ¾® 3 quand n  ¾® ¥ , 
donc f est d'ordre n² ou encore f est O(n²)

C'est cette notation que nous utiliserons pour mesurer la complexité temporelle C en nombre d'opérations élémentaires d'un algorithme fixé. Il suffit pour pouvoir comparer des complexités temporelles différentes, d'utiliser les mêmes fonctions g(n) de base. Les informaticiens ont répertorié des situations courantes et ont calculé l'ordre de complexité associé à ce genre de situation.

Les fonctions g(n) classiquement et pratiquement les plus utilisées sont les suivantes :
 
Ordre de complexité C Cas d'utilisation courant 
g(n) = 1  Þ C est O(1) Algorithme ne dépendant pas des données
g(n) = log (n) Þ C est O(log(n)) Algorithme divisant le problème par une quantité constante (base du logarithme)
g(n) = n  Þ C est O(n) Algorithme travaillant directement sur chacune des n données
g(n) = n.log(n) Þ C est O(n.log(n)) Algorithme divisant le problème en nombre de sous-problèmes constants (base du logarithme), dont les résultats sont réutilisés par recombinaison
g(n) = n² Þ C est O(n²) Algorithme traitant généralement des couples de données (dans deux boucles imbriquées).

     
  2. Trier des tableaux en mémoire centrale
 

Un tri est une opération de classement d'éléments d'une liste selon un ordre total défini. Sur le plan pratique, on considère généralement deux domaines d'application des tris: les tris internes et les tris externes.

Que se passe-t-il dans un tri? On suppose qu'on se donne une suite de  nombres entiers (ex: 5, 8, -3 ,6 ,42, 2,101, -8, 42, 6) et l'on souhaite les classer par ordre croissant (relation d'ordre au sens large). La suite précédente devient alors après le tri (classement) : (-8, -3, 2, 5, 6, 6, 8, 42, 42, 101). Il s'agit en fait d'une nouvelle suite obtenue par une permutation des éléments de la première liste de telle façon que les éléments résultants soient classés par ordre croissant au sens large selon la relation d'ordre totale " £ " : (-8 £ -3 £ 2 £ 5 £ 6 £ 6 £ 8 £ 42 £ 42 £ 101).

Cette opération se retrouve très souvent en informatique dans beaucoup de structures de données. Par exemple, il faut établir le classement de certains élèves, mettre en ordre un dictionnaire, trier l'index d'un livre, etc...
 

2.1 Tri interne, tri externe

Un tri interne s'effectue sur des données stockées dans une table en mémoire centrale, un tri externe est relatif à une structure de données non contenue entièrement dans la mémoire centrale (comme un fichier sur disque par exemple).

Dans certains cas les données peuvent être stockées sur disque (mémoire secondaire) mais structurées de telle façon à ce que chacune d'entre elles soitreprésentée en mémoire centrale par une clef associée à un pointeur. Le pointeur lié à la clef permet alors d'atteindre l'élément sur le disque (n° d'enregistrement...). Dans ce cas seules les clefs sont triées (en table ou en arbre) en mémoire centrale et il s'agit là d'un tri interne. Nous réservons le vocable tri externe uniquement aux manipulations de tris directement sur les données stockées en mémoire secondaire.
 
 

2.2 Des algorithmes classiques de tri interne

Dans les algorithmes référencés ci-dessous, nous notons  (a1, a2, ... , an) la liste à trier. Etant donné le mode d'accès en mémoire centrale (accès direct aux données) une telle liste est généralement implantée selon un tableau à une dimension de n éléments (cas le plus courant).

Nous attachons dans les algorithmes présentés, à expliciter des tris majoritairement sur des tables, certains algorithmes utiliserons des structures d'arbres en mémoire centrale pour représenter notre liste à trier (a1, a2, ... , an).

Les opérations élémentaires principales les plus courantes permettant les calculs de complexité sur les tris, sont les suivantes :
 


Ce sont ces opérations qui seront utilisées pour fournir une mesure de comparaison des tris entre eux.

Tris sur des tables : (suivez l'hyperlien pour consulter la page d'information du tri concerné)
 


Tris sur un arbre binaire : (suivez l'hyperlien pour consulter la page d'information du tri concerné)
 


 

3. Rechercher dans un tableau

Les tableaux sont des structures statiques contigües, il est facile de rechercher un élément fixé dans cette structure. Nous exposons ci-après des algorithmes élémentaires de recherche utilisables dans des applications pratiques par le lecteur.

Essentiellement nous envisagerons la recherche séquentielle qui convient lorsqu'il y a peu d'éléments à consulter (quelques centaines), et la recherche dichotomique dans le cas où la liste est triée.
 

3.1 Recherche dans un tableau non trié

Algorithme de recherche séquentielle :
  • Soit t un tableau d'entiers de 1..n éléments non rangés.
  • On recherche le rang (la place) de l'élément Elt dans ce tableau. L'algorithme renvoie le rang (la valeur -1 est renvoyée lorsque l'élément Elt n'est pas présent dans le tableau t) 
  • Complexité en O(n) 

Nous proposons au lecteur 4 versions d'un même algorithme de recherche séquentielle. Le lecteur adoptera une de ces versions en fonction des possibilités du langage avec lequel il compte programmer sa recherche.

Version Tantque avec "et alors" (si le langage dispose d'un opérateur et optimisé)

         i ¬  1 ;
        Tantque (i £ n) et alors (t[i] ¹ Elt) faire
                i ¬  i+1
        finTant;
        si  i £ n  alors rang ¬  i
        sinon rang ¬  -1
        Fsi

Version Tantque avec "et" (opérateur et non optimisé)

         i ¬  1 ;
        Tantque (i < n) et (t[i] ¹ Elt) faire
                i ¬  i+1
        finTant;
        si  t[i] = Elt alors rang ¬  i
        sinon rang ¬  -1
        Fsi

Version Tantque avec sentinelle en fin de tableau (rajout d'une cellule + opérateur et optimisé)

        t[n+1] ¬ Elt ; // sentinelle rajoutée
        i ¬  1 ;
        Tantque (i £ n) et alors (t[i] ¹ Elt) faire
                i ¬  i+1
        finTant;
        si  i £ n  alors rang ¬  i
        sinon rang ¬  -1
        Fsi

Version Pour avec instruction de sortie (conseillée si le langage dispose d'un opérateur Sortirsi)

        pour i ¬ 1 jusquà n faire
           Sortirsi t[i] =  Elt 
        fpour;
        si  i £ n  alors rang ¬  i
        sinon rang ¬  -1
        Fsi

 

 

3.2 Recherche dans un tableau  trié

Spécifications d'un algorithme séquentiel :
  • Soit t un tableau d'entiers de 1..n éléments rangés par ordre croissant par exemple.
    •  
  • On recherche le rang (la place) de l'élément Elt dans ce tableau. L'algorithme renvoie le rang (la valeur -1 est renvoyée lorsque l'élément Elt n'est pas présent dans le tableau t) On peut reprendre sans changement les versions de l'algorithme de recherche séquentielle précédent travaillant sur un tableau non trié.
    •  
  • Complexité moyenne en O(n)

On peut aussi utiliser le fait que le dernier élément du tableau est le plus grand élément et s'en servir comme une sorte de sentinelle. Ci-dessous deux versions utilisant cette dernière remarque.

Version Tantque

    si t[n] < Elt alors rang ¬  -1
    sinon
        i ¬  1 ;
       Tantque t[i] < Elt faire
                i ¬  i+1
        finTant;
        si t[n] = Elt alors rang ¬  i
        sinon
            rang ¬  -1
         Fsi
     Fsi

Version pour

    si t[n] < Elt alors rang ¬  -1
    sinon
       pour i ¬ 1 jusquà n-1 faire
           Sortirsi t[i] ³  Elt 
        fpour;
        si t[n] = Elt alors rang ¬  i
        sinon
            rang ¬  -1
         Fsi
     Fsi

Spécifications d’un algorithme dichotomique :
  • Soit t un tableau d'entiers de 1..n éléments rangés par ordre croissant par exemple.

    •  
  • On recherche le rang (la place) de l'élément Elt dans ce tableau. L'algorithme renvoie le rang (la valeur -1 est renvoyée lorsque l'élément Elt n'est pas présent dans le tableau t). Au lieu de rechercher séquentiellement du premier jusqu'au dernier, on compare l'élément Elt à chercher au contenu du milieu du tableau. Si c'est le même, on retourne le rang du milieu, sinon l'on recommence sur la première moitié (ou la deuxième) si  l'élément recherché est plus petit (ou plus grand) que le contenu du milieu  du tableau.

    •  
  • Complexité moyenne en O(log(n))
 

Soit un tableau au départ contenant les éléments (x1, x2, ... , xn)

On recherche la présence de lélément x dans ce tableau. On divise le tableau en 2 parties égales :


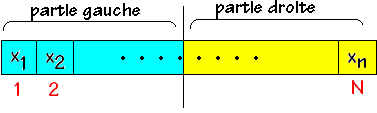
Soit x est inférieur à l' élément milieu et s'il est présent il ne peut être que dans la partie gauche, soit x est supérieur à l' élément milieu  et s'il est présent il ne peut être que dans la partie  droite. Supposons que x < milieu nous abandonnons la partie droite et nous recommençons la même division sur la partie gauche :

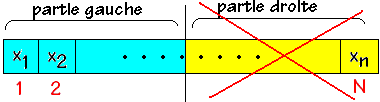
On redivise la partie gauche en deux parties égales avec un nouveau milieu :


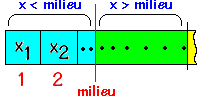
Si x < milieu c'est la partie gauche qui est conservée sinon c'est la partie droite etc ...

Le principe de la division dichotomique aboutit à la fin à une dernière cellule dans laquelle soit x = milieu et x est présent dans la table, soit x ¹ milieu  et x n'est pas présent dans la table.
 

  Version itérative de cet algorithme
     bas, milieu, haut, rang : entiers

     bas ¬  1; 
     haut ¬  N; 
     Rang ¬  -1; 
     repéter
        milieu ¬  (bas + haut) div 2; 
        si x = t[milieu] alors
            Rang ¬  milieu 
        sinonsi t[milieu] < x alors
                     bas ¬  milieu + 1 
                 sinon
                     haut ¬  milieu-1 
                fsi
       fsi
    jusquà ( x = t[milieu] ) ou ( bas > haut )
 

Voici en Pascal une procédure traduisant la version itérative de cet algorithme :
  
procedure dichoIter(x:Elmt; table:tableau; var rang:integer);
{recherche dichotomique par itération dans table rang =-1 si pas trouvé}
var
   milieu:1..max;
   g,d:0..max+1;

begin
  g := 1;
  d := max;
  rang := -1;
  while g <= d do
  begin
   milieu := (g+d) div 2;
   if x = table[milieu] then
   begin
     rang := milieu;
     exit
   end
   else
     if x < table[milieu] then d := milieu-1
     else g := milieu+1
  end;
end;{dichoIter}
  

Dans le cas de langage de programmation acceptant la récursivité (comme Pascal ), il est possible d'écrire une version récursive de cet algorithme dichotomique.

Voici en Pascal une procédure traduisant la version récursive de cet algorithme :
  
procedure dichoRecur(x:Elmt;table:tableau;g,d:integer;var rang:integer);
{ recherche dichotomique récursive dans table
   rang =-1 si pas trouvé.
   g , d: 0..max+1 }
var
   milieu:1..max;

begin
  if g<= d then
  begin
   milieu := (g+d) div 2;
   if x = table[milieu] then  rang := milieu
   else
     if x < table[milieu] then // la partie gauche est conservée
         dichoRecur( x, table, g, milieu-1, rang )
     else // la  partie droite est conservée
         dichoRecur( x, table, milieu+1, d, rang )
  end
  else rang := -1
end;{dichoRecur}